Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[3838] w	2014-02-26 20:09:27
B.4509 megfordításával adódik, hogy a húrnégyszög köré még egy parabola írható, melynek tengelye az eredeti paraboláéra merőleges, ezt és az eredeti parabolát elaffinítva további parabolákat kapunk, amik pedig B.4509 szerint húrnégyszögben metszik egymást, amely húrnégyszög az illeszkedéstartás szerint A'B'C'D'.
Előzmény: [3832] Sinobi, 2014-02-11 16:29:21

[3837] w

2014-02-26 20:01:14

Néhány témába illően szép feladat:

551. feladat. Adott egy AB szakasz, és egy e egyenes, ami áthalad a szakasz F felezőpontján. Rendelkezésünkre áll egy speciális szerkesztési eszköz, a szakaszfelező, ami két ismert ponthoz megrajzolja a tőlük egyenlő távol lévő pontok mértani helyét. Szerkesszünk csak szakaszfelezővel egy e-vel párhuzamos egyenest!

552. feladat. Nevezzünk egy k-alapú számrendszerbeli számot k-csökkenőnek, ha számjegyei balról jobbra olvasva szigorúan csökkennek.

(a) Van-e olyan n<100 pozitív egész úgy, hogy n bármely mn többszöröse a 10-csökkenő? (b) Van-e olyan n, amelyre igaz, hogy mn tetszőleges k-ra k-csökkenő? (c) Van-e végtelen sok ilyen n szám?

553. feladat. Legyenek a,b,n olyan pozitív egész számok, melyekre a¹⁰⁰+b¹⁰⁰ és a¹⁰⁴+b¹⁰⁴ osztható n-nel.

Igazoljuk, hogy a²⁰¹⁴+b²⁰¹⁴ is osztható n-nel!

[3836] Loiscenter	2014-02-19 23:02:31
köszönöm szépen azt hittem hogy nincs vége!
Előzmény: [3835] jonas, 2014-02-19 14:42:13

[3835] jonas

2014-02-19 14:42:13

Szerintem ez a szám a 1016949152542372881355932203389830508474576271186440677966, mert

6^.1016949152542372881355932203389830508474576271186440677966=

6101694915254237288135593220338983050847457627118644067796

Előzmény: [3833] Loiscenter, 2014-02-19 11:22:10

[3834] jonas	2014-02-19 14:29:40
Ilyesmit néztünk korábban ugyanebben a témában a [2271] hozzászólástól kezdve.
Előzmény: [3833] Loiscenter, 2014-02-19 11:22:10

[3833] Loiscenter

2014-02-19 11:22:10

szürgös:

Egy 6-ra végzödö szám ultolsó jegyét elhagyjuk. Ezt a szám elsö jegye elé irjuk. Az igy kapott szám hatsorosa az eredetinek. Melyik ez a szám? (azaz 6B = B6 . 6 ?)

[3832] Sinobi

2014-02-11 16:29:21

Sinobi: "b, Bizonyítsd be, hogy ha van egy parabolán három pontpár (húr), amelyek felezőmerőlegesei egy ponton mennek át, akkor ha a hat pontot a parabola tengelyirányában elaffinítjuk, akkor az így kapott pontok felezőmerőlegesei is egy ponton fognak átmenni."

Azota sem tudom. Kedvcsinalonak egy hasonlo, de nagyon egyszeru feladat:

Ha van egy parabolan egy ABCD hurnegyszog, azaz barmelyik 2 pont felezomerolegese atmegy egy O ponton, akkor ha a hurnegyszoget a parabola tengelyiranyaban affinitom, akkor az A'B'C'D' pontnegyes is hurnegyszog lesz, azaz barmelyik ket pont felezomerolegese at fog menni O'-n.

Ez ugyan kovetkezik az elozo allitasbol, de azt nem tudom belatni, meg egyszerubben is kijon.

Előzmény: [3795] Sinobi, 2013-10-12 01:30:53

[3831] w	2014-02-04 21:38:37
Az a) részt régi orosz versenyfeladat, a b) pedig egy kis gyakorlat, amit pont ennek a feladatnak az ötlete alapján találtam ki. :-)
Előzmény: [3830] Fálesz Mihály, 2014-02-04 20:43:33

[3830] Fálesz Mihály

2014-02-04 20:43:33

Egy kapcsolódó feladat 2007-ből:

A. 429. Határozzuk meg mindazokat az egész együtthatós f(x) és g(x) polinomokat, amikre f(g(x))=x²⁰⁰⁷+2x+1.

A tanulság valami olyasmi, hogy polinomba polinom $\implies$ deriválás... :-)

Előzmény: [3829] w, 2014-02-03 23:18:11

[3829] w

2014-02-03 23:18:11

550. feladat. (körülbelül)

a) Vannak-e olyan f,g,h másodfokú polinomok, melyekre az 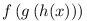$f\left(g\left(h(x)\right)\right)$ polinom pontosan az 1,2,3,4,5,6,7,8 helyeken nulla?

b) Határozzuk meg azokat az f,g,h polinomokat, melyekre 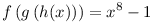$f\left(g\left(h(x)\right)\right)=x^8-1$ .

[Ezek nem nehéz, de érdekes feladatok. Ha eddig nem lett volna világos, aki ismeri őket, ne lője le. Aki maga megoldotta a feladatot, annak viszont szívesen látom megoldását.]

[3828] Loiscenter

2014-01-29 00:47:03

1. legyen x=y=0 => f(0) = 0; 2) legyen x=y => 4f(x)[ f(x) - x.x] = 0 => vagy f(x) = 0 vagy f(x)=x.x külön x értékre

3) minden t# 0 esetére ha f(t) = t.t # 0 => legyen x=0, y=t => f(t).f(-t) =f(t)f(t) => f(-t) = f(t)=t.t; ha f(t) = 0 => legyen x=0, y=-t => f(t).f(-t) =f(-t)f(-t) => f(-t) = f(t)=0 összefoglalva f(-x)=f(x) minden x estére.

4) Ha létezik a# 0 ugy , hogy f(a)=0 => akkor minden t# 0 esetére legyen x=t, y=a => f(t+a)f(t-a) = f(t)f(t) legyen x=a, y=t => f(t+a)f(a-t) = f(t)f(t) - 4a.a.f(t) Mivel f(t-a) = f(a-t) => 4a.a.f(t) = 0 => f(t)=0

összegezve : f(x)=0 és f(x) = x.x; a két valosfüggvény , amely teljesiti a feltételt.

(Prof. Hung Son Nguyen - Varso egyetemból)

Előzmény: [3827] Loiscenter, 2014-01-28 20:46:14

[3827] Loiscenter	2014-01-28 20:46:14
tényleg nincs folytonosság! igy csak 0 vagy x.x maradt! hogy tovább?
Előzmény: [3825] nadorp, 2014-01-28 15:33:25

[3826] w	2014-01-28 15:37:28
Keresd meg az összes olyan f:R $\to$ R függvényt, melyre f(x)²=1 teljesül minden x-re.
Előzmény: [3824] Loiscenter, 2014-01-28 15:17:44

[3825] nadorp

2014-01-28 15:33:25

Ez így egy kicsit hiányos.

Ugyanis abból, hogy minden x-re f²(x)=x²f(x) teljesül, csak az következik, hogy f(x)=0 vagy f(x)=x², de ez még nem zárja ki azt, hogy pld f(2)=4 és f(5)=0 egyszerre teljesüljön.

Előzmény: [3824] Loiscenter, 2014-01-28 15:17:44

[3824] Loiscenter	2014-01-28 15:17:44
Legyen x=y=0 akkor f(0)=0 . legyen x=y igy f(2x)f(0)=4f(x)f(x) -4x.x.f(x) mivel f(0)=0 ezért 4f(x)f(x)-4x.x.f(x)=0 téhats f(x)=0 vagy f(x)=x.x . ellenörizve igaz mind.( bocsi nem tudtam hatványt irni)
Előzmény: [3822] w, 2014-01-27 22:06:36

[3823] Ménkűnagy Bundáskutya	2014-01-27 22:57:22
Ez tetszik, jóféle. :)
Előzmény: [3822] w, 2014-01-27 22:06:36

[3822] w

2014-01-27 22:06:36

Egy "vicces" függvényegyenlet.

Keressük meg az összes f:R $\to$ R függvényt a következő tulajdonsággal:

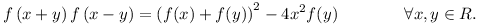
$f\left(x+y\right)f\left(x-y\right)=\left(f(x)+f(y)\right)^2-4x^2f(y)\qquad\qquad\forall x,y\in R.$

[3821] aaaa

2014-01-26 22:07:48

Ebből még az is következik, hogy:

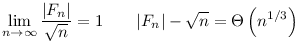
$\lim_{n\to\infty}\frac{|F_n|}{\sqrt{n}}=1\qquad |F_n|-\sqrt{n}=\Theta\left(n^{1/3}\right)$

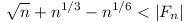Ugyanis n $\geq$ 64-re $\sqrt{n}+n^{1/3}-n^{1/6}<|F_n|$ , mert van legalább egy 5-ik hatvány, egyébként finomítva a becslésedet (prímedik hatványokra elég nézni az összeget):

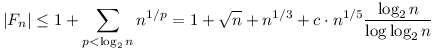
$|F_n|\leq 1+\sum_{p<\log_2n} n^{1/p}=1+\sqrt{n}+n^{1/3}+c\cdot n^{1/5}\frac{\log_2 n}{\log\log_2 n}$

Ugyanis n-ig a prímek száma kb 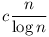$c\frac{n}{\log n}$ , ebből látszik, hogy elég nagy n-re

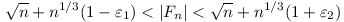
$\sqrt{n}+n^{1/3}(1-\varepsilon_1)<|F_n|<\sqrt{n}+n^{1/3}(1+\varepsilon_2)$

Előzmény: [3817] Ménkűnagy Bundáskutya, 2014-01-26 15:42:40

[3820] w

2014-01-26 21:23:19

Az a sor talán jobban érthetően:

$|F_n|\le1+\sum_{k=2}^{[\log_2 n]}n^{1/k}$

után ugye n^1/k $\le$ n^1/2 igaz minden k $\ge$ 2-re, vagyis az összeg minden tagját (ebből [log₂n]-1 darab van) n^1/2-re cserélve ez kisebb, mint $1+n^{1/2}\cdot\left([\log_2 n]-1\right)<1+n^{1/2}\log_2 n$ .

Előzmény: [3819] Loiscenter, 2014-01-26 20:25:37

[3819] Loiscenter	2014-01-26 20:25:37
a bizonyitasod tényleg nagyon jonak latszik, csak még nem latom hogy egyenlötlenség masodik része miért ?
Előzmény: [3817] Ménkűnagy Bundáskutya, 2014-01-26 15:42:40

[3818] Loiscenter	2014-01-26 20:14:21
nagyon szép a magyarazat! köszönöm szépen!
Előzmény: [3816] aaaa, 2014-01-26 02:07:38

[3817] Ménkűnagy Bundáskutya

2014-01-26 15:42:40

Azt hiszem, van egyszerűbb is.

Az n-nél kisebb k. hatványok száma legfeljebb n^1/k. Itt a k legfeljebb log₂n lehet: eltekintve az 1-től a 2 log₂n. hatványával még számolni kell, többel biztosan nem. Azaz

|F_n| $\leq$ n^1/2+n^1/3+...+n^1/log₂n+1 $\leq$ n^1/2log₂n+1,

ami n-nel osztva nyilván 0-hoz tart.

Előzmény: [3815] aaaa, 2014-01-26 01:23:52

[3816] aaaa	2014-01-26 02:07:38
Természetesen $\tau=\frac{1}{2}\log\left(1+\frac{\varepsilon-\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)>0$ választással élünk.
Előzmény: [3815] aaaa, 2014-01-26 01:23:52

[3815] aaaa

2014-01-26 01:23:52

Gondolom azt szeretnéd kérdezni, hogy ha F_n={n-nél kisebb hatványszámok}, akkor mi lesz

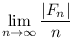
$\lim_{n\to\infty}\frac{|F_n|}{n}$

Lemma 1. $\forall$ $\varepsilon$ , $\delta$ >0 $\exists$ k₀, hogy k>k₀ esetén:

$\left|\sum_{i=k}^{[k(1+\varepsilon)] }\frac{1}{i}-\log(1+\varepsilon)\right|<\delta$

Ez a szokásos integrálós becslésből kijön, legyen ez házi feladat.

Lemma 2. Ha a_i pozitív egészek egy növekvő részsorozata, és 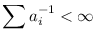$\sum a_i^{-1}<\infty$ , akkor n^-1|A_n| $\to$ 0, ha n $\to$ $\infty$ , ha A_n={a_i|a_i<n}

Indirekt, tegyük fel, hogy nem áll fent a bemutatott egyenlőség, vagyis létezik olyan $\varepsilon$ , hogy |A_n|> $\varepsilon$ n végtelen sokszor. Ha nincs ilyen, akkor pont azt kaptuk, amit akartunk. Legyen $H_\varepsilon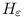$ az ilyen n-ek halmaza, ekkor |H|=|N|, vegyük tehát egy olyan b_i részsorozatát, ami tudja azt, hogy $\varepsilon$ ^kb_i>b_i-1, valamely k>2 egészre. Ekkor A_{b_i}> $\varepsilon$ b_i miatt a [0,b_i-1] intervallumba maximum b_i-1< $\varepsilon$ ^kb_i<A_{b_i} $\varepsilon$ ^k-1 darab eshet, szóval elég kevés szám, vagyis a számok legalább 1- $\varepsilon$ ^k-1-edrésze a jó intervallumba esik. De ekkor az ide eső számok reciprokösszegére alsó becslést ad, ha az intervallumba eső legkisebb számokat vesszük, ebből legalább A_{b_i}-A_{b_i-1}=b_i( $\varepsilon$ - $\varepsilon$ ^k-1) darab van:

$\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq\sum_{i=[b_i-b_i \varepsilon+\varepsilon^k]}^{b_i}\frac{1}{i}\geq \log\left(1+\frac{\varepsilon-\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)-\delta$

Az első lemma alapján. De legyen b₁ akkora, hogy 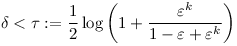$\delta<\tau:=\frac{1}{2}\log\left(1+\frac{\varepsilon^k}{1-\varepsilon+\varepsilon^k}\right)$ teljesüljön, így azt kaptuk, hogy $\sum_{a_j\in]b_{i-1},b_i]}\frac{1}{a_j}\geq \tau>0$ De ekkor

$\sum_{a_i<b_k} a_i^{-1}=\sum_{j=1}^{k}\sum_{a_i\in]b_{j-1},b_j]}\frac{1}{a_j}\geq\sum_{j=1}^{k}\tau=k\tau$

Viszont így a reciprokösszeg nem lehet véges.

Lemma 3. A hatványszámok reciprokösszege kisebb, mint 2. Nézzük ugyanis a kövezkező összeget:

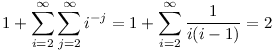
$1+\sum_{i=2}^\infty\sum_{j=2}^\infty i^{-j}=1+\sum_{i=2}^\infty\frac{1}{i(i-1)}=2$

Viszont a^b szerepel az a számhoz tartozó részlegösszegben, szóval a hatványszámok reciprokösszege véges.

Lemma 3 miatt teljesül Lemma 2. feltétele, így a hatványszámok felső sűrűsége 0 az egészek körében.

Előzmény: [3814] Loiscenter, 2014-01-24 20:30:06

[3814] Loiscenter	2014-01-24 20:30:06
Hatványszámok valoszinüsége természetes számok körében?

Már regisztráltál?
Új vendég vagy?