Fórum: Érdekes matekfeladatok

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161]

Szeretnél hozzászólni? Jelentkezz be.

[47] lorantfy	2003-11-10 11:21:06
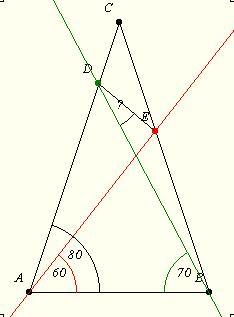
Egy ábra a lenti feladathoz. (Imádom az Euklides programot!)

[46] jenei.attila	2003-11-10 10:44:46
Egy geometria feladat: Az ABC egyenlő szárú háromszög AB alapon fekvő szögei 80 fokosak. A-ból az alappal 60 fokos szöget bezáró egyenes a BC szárat E pontban, B-ből az alappal 70 fokos szöget bezáró egyenes az AC szárat D pontban metszi. Mekkora az EDB szög?

[45] Hajba Károly

2003-11-10 01:19:09

> köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt

Tanulom a TeX-et. :o)

> Te biztosan emlékszel még a RUBIK kockára

Mi az, hogy emlékszem! Engem a gimi 3. osztályában ért (ma 11. o.), s a kockám nemegyszer a tanári asztalon vészelte át az óra második felét több más kockával egyetemben. Így az ábrád öt percnyi tanulmányozása után rájöttem a "trükk"-re, de hagyok mást is gondolkodni.

Előzmény: [43] lorantfy, 2003-11-08 15:50:59

[44] Lóczi Lajos	2003-11-09 16:21:43
Valóban, ez így szép és jó. Utólag természetesen a "mi" formulánkat is megtaláltam, pl. a http://mathworld.wolfram.com/RiemannZetaFunction.html oldalon ez a (23)-as formula :-) Érdemes megnézni, van néhány szép ábra (és csaknem 100 egyéb dzeta-képlet)...
Előzmény: [40] Pach Péter Pál, 2003-11-07 23:14:59

[43] lorantfy

2003-11-08 15:50:59

Kedves Károly!

Gratulálok a megoldáshoz és köszönöm, hogy ilyen szép táblázatos formában feltetted az eredményt!

Te biztosan emlékszel még a RUBIK kockára és remélem, hogy a fiatalabbak is ismerik. Nekem nagy sikerélmény volt, hogy meg tudtam oldani. 3 napom ment rá egy téli vizsgaidőszakban és meg is lett az eredménye, 4-es lett az analízis vizsgám… A következő nyáron Angliában jártam és ott lehetett kapni a Rubik kocka mindenféle változatát. Vettem is egy nyolcszög alapú hasáb alakút és összekeverés után a begyakorolt transzformációkkal próbáltam visszaforgatni az alaphelyzetbe. Rejtélyes módon az alábbi eredményre jutottam: egy élközépen lébő kocka megfordult a többi mind a helyére került. 9. feladat : Hogyan lehetséges ez?

[42] Hajba Károly

2003-11-08 00:46:23

Kedves László!

Igazad van, én is megtaláltam az 5 megoldást.

K	L	M	N
2	3	7	41
2	3	8	23
2	3	9	17
2	4	5	19
2	4	6	11

Előzmény: [38] lorantfy, 2003-11-06 23:19:20

[41] lorantfy

2003-11-08 00:39:03

Kedves Fórumosok !

Örülök, hogy ilyen sokan foglalkoztatok a biliárdgolyós példával, még idemásolok egy megoldást, ami felhasználja ugyan az előbbi mérés eredményét, de talán annak aki később idetéved érthetőbb:

A 12 golyót 3 4-es csoportra bontom.

OOOO OOOO OOOO

Két 4-es csoportot összehasonlítok a mérleggel (1. mérés)

OOOO -- OOOO

1.1. Egyenlők: ekkor a maradék 4 között van az eltérő

OOOO = OOOO HHHH

Veszek 2-t az első 8 golyó közül (ezek jók) és 2-t a maradék 4-ből

OO -- HH HH

Összemérem őket (2. mérés),

1.2. Ha lebillen a mérleg akkor a mérlegen lévő kettő (HH) közül a 3. méréssel eldöntöm melyik az eltérő golyó.

1.3. Ha egyenlő a 2. mérés eredménye akkor a nem mért 2 közül (HH) döntök a 3. méréssel. (Egyiket összemérem egy jó golyóval)

2.1. Ha a két 4-es csoport összemérésekor lebillen a mérleg. Ekkor amerre lebillent azt a 4 golyót N betűvel jelölöm ( ezek között lehet egy nehezebb)a másik oldalon lévő 4-et K betűvel jelölöm (ezek között lehet egy könnyebb)

Pl.: KKKK < NNNN OOOO

2.2. Bal oldalra felteszek a mérlegre 3 db K jelű golyót és 1 db N jelűt, jobb oldalra pedig 1 db (a megmaradt) K jelűt és a 3 db biztosan jó golyót. (Még 3 db N jelű és egy jó (O) marad ki)

KKKN -- KOOO NNN O

Nézzük az eseteket:

3.1. Ha a mérleg jobbra billen le. Ekkor a bal oldali 3 K közül 1 golyó könnyebb.

KKKN < KOOO NNN O

Ezek közül egy méréssel tudok dönteni, hiszen tudom, hogy a hibás golyó könnyebb. Kettőt összemérek, amelyik felemelkedik az a hibás. Ha egyenlő a kettő összemért, akkor a 3. a hibás golyó.

3.2. Ha a mérleg egyensúlyban marad akkor a kimaradt 3 db N jelű golyó

KKKN = KOOO NNN O

között van egy nehezebb, amit a 3. méréssel az előzőhöz hasonlóan el lehet dönteni.

3.3. Ha a mérleg balra billen ki, akkor ezt okozhatja a bal oldali N jelű golyó vagy a jobb oldalon lévő K jelű golyó.

KKKN > KOOO NNN O

Ezt a 3. méréssel könnyen el lehet dönteni, ha pl. a K jelűt összemérem egy jó golyóval. Ha felemelkedik akkor ez a hibás, ha egyenlők, akkor az N jelű.

[40] Pach Péter Pál

2003-11-07 23:14:59

A 8. feladatra írok megoldást, úgyhogy, aki még nem oldotta meg (és szeretne rajta gondolkozni), ne olvassa tovább. Tekintsük a következő átalakításokat:

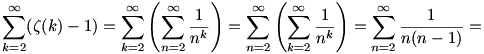
$\sum_{k=2}^{\infty} (\zeta(k)-1)=\sum_{k=2}^{\infty} \left(\sum_{n=2}^{\infty} \frac1 {n^k}\right)=\sum_{n=2}^{\infty} \left(\sum_{k=2}^{\infty} \frac1 {n^k}\right)=\sum_{n=2}^{\infty} \frac1 {n(n-1)}=$

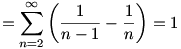
$=\sum_{n=2}^{\infty} \left (\frac1 {n-1}-\frac1 {n} \right)=1$

Pozitív számokat összegzünk, és a határérték valóban létezik (olvassuk az átalakításokat hátulról visszafelé), így nem "csaltunk", amikor megcseréltük a két szummát. Ezen kívül a mértani sor összegképletét, és egy ún. "teleszkópos trükköt" alkalmaztunk.

Az előbb bizonyított állítás nyilvánvaló következménye, hogy

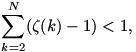
$\sum_{k=2}^N (\zeta (k)-1) <1,$

ugyanis az előbbi összegnek van olyan tagja, ami ebben az összegzésben nem szerepel. (Mint már megállapítottuk, minden tag pozitív: 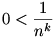$0<\frac1 {n^k}$ )

Pach Péter Pál

Előzmény: [30] Lóczi Lajos, 2003-11-05 23:59:16

[39] lorantfy	2003-11-07 09:56:01
A biliárdgolyós példa alábbi megoldását Gáti Beatrix küldte nekem.

[38] lorantfy	2003-11-06 23:19:20
Kedves Csillag! Nagyon szép a megoldásod, gratulálok! Holnap felteszek hozzá egy táblázatot, hogy mikor melyik golyó jön ki, igy mindenki ellenőrizheti, hogy jó is. Elemben a tevés példán gondolkodók még keresgélhetnek, ha van idejük, mert én 5 megoldást találtam.

[37] Csillag	2003-11-06 16:02:59
A billiárdgolyós probléma mindkét nehezített változatát megoldja a következő három mérés. Ezzel 12 golyó esetén meghatározható, hogy melyik volt hibás és hogyan, 13 golyó esetén pedig, hogy melyik volt hibás: 1.mérés: (x1,x2,x3,x4) összehasonlítása (x5,x6,x7,x8)-cal 2.mérés: (x1,x2,x5,x11) összehasonlítása (x3,x6,x9,x10)-zel 3.mérés: (x1,x6,x9,x11) összehasonlítása (x3,x4,x7,x12)-vel
Előzmény: [20] Kós Géza, 2003-11-05 12:21:41

[36] Kós Géza

2003-11-06 14:24:35

Kedves Csimby,

Amit írtatok, az mindenképpen megérdemel egy fél Túró Rudit, de jobb lenne egy szép, világos, kerek megoldássá átírni. Ehhez pontosabban kell kezelni a falvak és a hittérítők lehetséges állapotait.

Előzmény: [23] Csimby, 2003-11-05 18:21:35

[35] lorantfy	2003-11-06 14:18:01
Az eredeti tevés példa úgy szólt, hogy 11 tevét örökölnek és hogyan oszthatnák el ha a legidősebb felét, a középső harmadát, a legkisebb hatodát örökölte. És a bölcs kádi javaslatára kölcsönkérnek egy tevét, amit az osztozkodás után vissza is adnak.

[34] Fálesz Mihály	2003-11-06 13:06:27
Ha jól értem, a végén maradnia kell egy tevének, amit visszadanak.
Előzmény: [31] Rizsa, 2003-11-06 12:27:26

[33] Hajba Károly	2003-11-06 12:43:32
Hát igen! Mivel a reciprokösszeg lehet 1,0 is, ezért ezt elnéztem, tehát ezek szerint 3 megoldást találtunk eddig.
Előzmény: [32] Hajba Károly, 2003-11-06 12:31:28

[32] Hajba Károly

2003-11-06 12:31:28

A 7. feladathoz:

Először is elnézést mindenkitől, de még nem sikerült elmélyedni a TeX-ben, így annak lehetőségeit most nem használom ki. (De ami késik, nem múlik.)

Mivel a tevék számához még 1-t hozzáadva el tudták osztani kényelmesen és még meg is maradt a kölcsönteve, ezért a K, L, M számok reciprokösszege alulról közelíti az 1-t, de nagyobb mint a legkisebb elérhető N-re N/(N+1)=0,9; ahol N=2+3+4=9. (Lehet ennél finomabban is lehatárolni.)

Tehát azokat a számhármasokat kell megvizsgálni, melyek reciprokösszege ebbe a tartományba esik. K=2, mivel a 3, 4, 5 számhármasra 0,78..; továbbá 2, 4, 5 számhármasra 0,8666... jön ki, mint alsó korlát, másrészről 2, 3, 6 számhármasra 1,00 jön ki, mint felső korlát. Én a két számhármas között két megoldást találtam:

K=2, L=3, M=7, N=41

K=2, L=4, M=6, N=11

Hajba Károly

Előzmény: [26] lorantfy, 2003-11-05 21:34:18

[31] Rizsa	2003-11-06 12:27:26
A tevel szama 17, es 2, 3, 6 reszre kell bontani a majdani 18at.

[30] Lóczi Lajos

2003-11-05 23:59:16

Mivel közben sikerült tisztáznom az előző hozzászólásban megfogalmazott sejtésem (a bizonyítás nem nehéz, teljesen elemi, csak két apró ötlet kell, és minden szükséges információ megtalálható a hozzászólásban), ezért

8. feladat: Mutassuk meg, hogy tetszőleges N $\ge$ 2 természetes számra

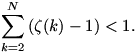
$\sum_{k=2}^N \left(\zeta(k)-1\right)<1.$

Előzmény: [29] Lóczi Lajos, 2003-11-05 23:20:59

[29] Lóczi Lajos

2003-11-05 23:20:59

Az 1. feladattal kapcsolatban a következő érdekes általánosítás tűnik igaznak: nevezetesen nem számít, hogy mely hatványfüggvények reciprokait szerepeltetjük a szummákban (ami ott 2, 3, 5, illetve 8 volt). A rövidség kedvéért vezessük be a következő (szokásos) jelölést: ha s>1 valós szám, akkor legyen

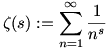
$\zeta(s):=\sum_{n=1}^{\infty}\frac{1}{n^s}$

a híres-nevezetes dzeta-függvény. (Mint ismeretes, ennek a függvénynek komplex s-ekre történő kiterjesztése szerepel az egyik leghíresebb, mindmáig megoldatlan matematikai sejtésben, a Riemann-hipotézisben.)

Ezzel a jelöléssel az előző hozzászólásban beláttuk tehát, hogy

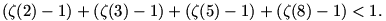
$\left(\zeta(2)-1\right)+\left(\zeta(3)-1\right)+\left(\zeta(5)-1\right)+\left(\zeta(8)-1\right)<1.$

Sejtésem a következő: 2-től kezdve akárhány ilyen tagot adunk össze, az összeg mindig kisebb lesz 1-nél, azaz, ha N $\ge$ 2 tetszőleges természetes szám, akkor

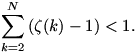
$\sum_{k=2}^N \left(\zeta(k)-1\right)<1.$

A sejtést alátámasztják a Mathematica programmal végzett numerikus kísérletek (például ha N=50, akkor a fenti összeg körülbelül 0,99999999999999911...), valamint a Mathematica azon állítása, hogy

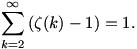
$\sum_{k=2}^{\infty} \left(\zeta(k)-1\right)=1.$

(Ha a program ezt állítja, akkor valószínűleg ezt már bebizonyította valaki, a sejtéshez nyilván "elég" lenne ez utóbbi állítást megmutatni, hiszen a szumma N-ben monoton nő.)

A sejtéssel kapcsolatos bármely észrevételt szívesen veszek.

[28] Lóczi Lajos

2003-11-05 22:56:02

Ha szabad integrálokat használni, akkor következzen egy megoldás az 1. feladatra.

Mivel az összegzendő kifejezések szigorúan monoton fogyóak, ezért felfoghatók integrálok alsó (téglalapos) közelítőösszegeiként -- csak arra kell vigyáznunk, hogy az integrálás határát 1-gyel hamarabb kezdjük, mint a szummázásét. (A szumma első két tagját külön kell kezelnünk, mert különben felső becslésünk túl durva lenne.) Tehát

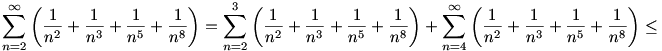
$\sum_{n=2}^{\infty}\left(\frac{1}{n^2}+\frac{1}{n^3} +\frac{1}{n^5}+\frac{1}{n^8}\right)= \sum_{n=2}^{3}\left(\frac{1}{n^2}+\frac{1}{n^3} +\frac{1}{n^5}+\frac{1}{n^8}\right)+ \sum_{n=4}^{\infty}\left(\frac{1}{n^2}+\frac{1}{n^3} +\frac{1}{n^5}+\frac{1}{n^8}\right)\le$

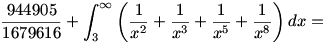
$\frac{944905}{1679616}+\int_{3}^{\infty}\left(\frac{1}{x^2}+\frac{1}{x^3} +\frac{1}{x^5}+\frac{1}{x^8}\right)dx=$

$\frac{944905}{1679616}+\left[-\frac{1}{x}-\frac{1}{2x^2} -\frac{1}{4x^4}-\frac{1}{7x^7} \right]_3^\infty= \frac{944905}{1679616}+\left( 0+\frac{24007}{61236}\right)=$

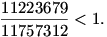
$\frac{11223679}{11757312}<1.$

Előzmény: [1] Sirpi, 2003-10-30 10:07:33

[27] Lóczi Lajos

2003-11-05 22:15:39

A már említetteken kívül pár egyéb "ötlet" a tréfás kérdés megválaszolásához.

Az e^x függvényen kívül a (konstans^.e^x) függvény, mint általános megoldás is szóba jöhet (abban az értelemben, hogy a függvény és deriváltja megegyezik).

Speciálisan a kuncogó függvény lehet az azonosan nulla függvény is.

De kuncoghat azért is, mert ő mondjuk a Dirichlet-függvény (amely tehát racionális pontokban 1, irracionálisokban 0, s így sehol sem folytonos, sehol sem deriválható).

Sőt, kuncoghat azért is, mert ő pl. az x² függvény, s így deriválás után az értékkészlete nagyobb lesz.

Előzmény: [11] enel, 2003-11-04 14:32:31

[26] lorantfy

2003-11-05 21:34:18

Valamikor régen amikor a Scientific American még Tudomány néven magyarul is megjelent olvastam benne egy matek feladványt. De sajnos ez olyan régen volt, hogy a pontos számokat már elfelejtettem, így kénytelen vagyok a feladatot általánosan megfogalmazni: 7. feladat: A gazdag tevekereskedő mielőtt meghalt magához hívta 3 fiát és elmondta nekik, hogy rájuk hagyja N db tevéjét. A tevék K-ad részét a legidősebb, L-ed részét a középső és M-ed részét pedig a legkisebb fia kapja. A kereskedő halála után a fiúk bajban voltak mert az N szám K, L, M egyikével sem volt osztható. Szerencsére éppen egy tevekaraván haladt át a falun és a legkisebb fiúnak támadt egy ötlete. Kölcsönkért egy tevét a karavánból. Így az N+1 tevét el tudták osztani egymás között a végakaratnak megfelelően és még maradt is 1 teve, amit visszaadtak a tulajdonosának. Milyen K,L,M,N számokra teljesíthető a fenti felosztás ? ( K<L<M<N pozitív egész számok!)

[25] Kritya3	2003-11-05 20:47:52
Most egy kicsit offolok, remélem nem orrol meg rám a Moderátor: olyat hallottam, hogy OKTV napján a versenyig még egy számot sem szabad összeadni.
Előzmény: [21] Frenky, 2003-11-05 15:56:04

[24] Rácz Béla

2003-11-05 19:04:54

Ha valakit szétvetne a kíváncsiság, közölhetem, hogy az összes eddigi kétkarú mérleges feladat megtalálható a Skljarszkij-Csencov-Jaglom: Válogatott feladatok és tételek az elemi matematika köréből c. gyűjteményben (I. kötet, rögtön az eleje.)

Igazából ezt a könyvajánlóba kellett volna írnom, mert a Skljarszikij messze a legjobb matekkönyv, ami valaha is a kezembe került. Szovjet minőség!!! ;-)

Előzmény: [20] Kós Géza, 2003-11-05 12:21:41

[23] Csimby

2003-11-05 18:21:35

MEGOLDÁS A SZIGETES FELADATHOZ:

Akkor esznek meg egy papot amikor a legközelebbi olyan faluba ér ahonnan egy társa indult (ha egyedül van akkor amikor az indulási faluba visszaér). Tehát ha kezdetben P pap indult, amikorra mindet megeszik, P falu lesz pogány méghozzá az a P amelyből indultak (hiszen egészen addig nyugodtan téríthet egy pap amíg indulási helyre nem ér, ahol is hívő falut talál: -> megeszik, az indulási falu pogány lesz. -> az addig útbaeső falvakat megtéríti*. Az utánuk indulók, mivel nem indulhatnak a meglévő pogány falukból (hiszen ezek induló faluk voltak és mindenki más faluból indul) biztosan olyan faluból kell, hogy induljanak amelyeket már megtérítettek, tehát amint elindulnak, rögtön megeszik őket. Mindenki máshonnan indul, tehát mindenkit máshol esznek meg, tehát mindegyik falu pogány lesz. * probléma akkor lehet, ha a P db pap indulása után még indulnak valamikor pap(ok), de ez még az előtt történik, hogy kialakulna az a helyzet amikor már csak a P db indulási falu pogány (azaz amikor még lehet olyan helyekről indulni amelyet még senki sem térített meg). Ekkor két eset lehet: - az induló már megtérített faluból indul -> meghal rögtön, és a falu pogány lesz - pogány faluból indul (amelyben előtte még senki sem járt) , ekkor felfoghatjuk úgy mintha P+1 pap indult volna, és ugyanaz a megoldás mint P-re.

Kiss Gábor és Csajbók Bence

Már regisztráltál?
Új vendég vagy?