| [523] Maga Péter | 2004-10-09 22:04:22 |
 Üdv mindenkinek!
Egy szép feladat (sajnos nem saját):
Bizonyitsuk be, hogy minden n>1 egészre
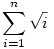 irracionális! irracionális!
|
|
| [522] Suhanc | 2004-10-09 13:34:46 |
 Kedves Onogur!
Hát itt eléggé begyorsultak a hozzászólások,és már nem nagyon követtem... a 103. feladatodra viszont, ha jól láttam, még nem válaszolt senki! Először is: Nagyon ötletes!!!:) Ha saját, akkor őszintén gratula! Ha láttad valahol, leírnád, hol találok még ilyeneket? /ja, és ha nem probléma, ezt is "elkérném" matekórára ;D/
A megoldásom:
A 6. állítás nyilvánvalóan hamis! Tehát 6-os nincs a számban, az azonban osztható hattal! Ebből az is következik, hogyaz első állítás is hamis, tehát egyes sincs benne!
Innen esetszétválasztással oldjuk meg!
Tfh: a 2. állítás igaz!Ekkor 0 nem lehet benne, mert az csak a legelső helyre kerülhetne! Tehát a 0. álllítás is hamis!
Ha minden számjegy kisebb, mint a következő, akkor nincs két egyforma, tehá a hármas állítás is igaz, így a számban 3-as is van! Ezzel megcáfoltuk a nyolcas állítást, mert 3-2=1! Tehát nyolcas nincs benne!
A negyedik állításnak hamisnak kell lennie,különben az ötös állítás hamis, tehát a szám legalább 6 jegyű, de csak a 2;3;4 számjegyek építik fel, és nincs ismétlődés! Ez nyilvánvalóan lehetetlen. Az ötös állítás viszont igaz, mert 5 féle számjegyet (0; 1;4;6;8) már kizátunk, és nem lehet ismétlődés!!! Ekkor a 9. állítás is igaz, mert 2+3=5! Mivel az eddig kiválasztott számok (2;3;5;9), és a még nem vizsgált számok (7) között csak a 2 a páros, és az sem állhat a végén( a második állítás miatt), ezért a 7. állítás nem igaz! Ekkor a 2;3;5;9 számokból felépülő egyetlen lehetsége megoldás a 2359! Ez azonban tesz eleget a 0., hamis állításnak, tehát ez sem jó megoldás!!!
Ha a 2. állítás hamis:
Ha a 8. állítás hamis lenne, akkor a 4. állítás biztosan igaz lenne, mert csak a 3 4;5 számok vannak egymás mellett azok közül, amelyeket még nem lőttünk ki! Ha 4 igaz, akkor 5;7,9 hamisak,ezért a 3. igaz, ekkor azonban az 5. állítás hamissága miatt ellentmondásra vezet!()hasonlóan az előző esethez!)
Tehát a 8.állítás igaz! Emiatt a 7. és a 9.állítás hamis, valamint a 8. állítás igaza megcáfolja a 4. állítást, ezért a is hamis!
Összesítve: ez esetben ídáig 1;2;4;6;7;9 hamisak, és 8 igaz! Ekkor nem lehet 3 és 5 is igaz, mert akkor 3+5=8, és ekkor 9 igaz lenne! De mindkettő hamis sem lehet, mert akkor nem lesz PN számjegy a számban, és akkor 7. igaz lenne!
Ha 5. hamis, és 3. igaz, akkor legfeljebb 3 számjegyből áll a szám(0;3;8), és 5. hamissága miatt leglább hatjegyű, persze, ismétlés nélkül!:D Tehát ez megint ellentmondás!
Tehát 5.igaz, és 3. hamis!
Mivel a szám 6-tal osztható, ezért kell lennie 0-s számjegynek is! Mievl 3. hamis, ezért van ismétlődő számjegy! Azonban 5 vagy 8 nem ismétlődhet, mert akkor 5+0=5 és 9. igaz lenne! Ugyanezen okokmiatt nem leht a számban 3db 0! Ezen okok miatt az egyetlen lehetséges megoldás 8005!!!
|
| Előzmény: [497] Hajba Károly, 2004-10-06 09:07:13 |
|
|
|
|
|
| [517] Lóczi Lajos | 2004-10-09 00:16:21 |
 Olyan is van sok. Az 19860311 után következő legközelebbi ilyen prímek, amelyek tehát születési dátumként is értelmezhetők, és megfelelnek a feladat kritériumának: 19860727, 19870831, 19900403, 19910809, 19920713, stb...
Persze hogy nem fejben számoltam:) A következő egyszerű Mathematica-utasítás kész formában adja az eredményt (az eredeti feladatét, nem a "dátumosét"; az utasítás vége felé lehet beállítani, hogy hányadik prímtől hányadikig vizsgálja át a prímeket - itt olyan határokat adunk meg, hogy a 8-jegyű prímek között maradjunk...)
Prime[Drop[ Union[Table[ If[{a, b, c, d, e, f, g, h} = IntegerDigits[Prime[n]]; PrimeQ[FromDigits[{a, b, c, d, e, f, g, h, a, b, c, d, e, f, g, a, b, c, d, e, f, a, b, c, d, e, a, b, c, d, a, b, c, a, b, a}]], n], {n, 1265000, 1266000}]], -1]]
|
| Előzmény: [515] SAMBUCA, 2004-10-08 23:36:51 |
|
| [516] Hajba Károly | 2004-10-09 00:08:04 |
 Kedves Sambuca!
Te keresésben jó vagy, de gondolom az agyad is élesre van köszörülve, így remélhetőleg tudsz segíteni a következő probléma megoldásában is, melyet előre is megköszönök Neked.
Nos Vízi Dávid hozott a 98. feladatban [472] egy - számomra mindenképpen - érdekes problémát, melyet innen merített. N=5-re feltehetően nincs már jobb megoldás, de szerintem n=7-re vagy n=13-ra létezik jobb megoldás is. Olyan snassz, hogy csak téglatestek vannak lepakolva. Titkolják vagy még nem találták meg? Nem jobban néznének ki az ábrák, ha ez lenne aláírva:
Found by SAMBUCA in 2004 vagy esetleg Found by Onogur in 2004. :o)
Mit gondolsz, s(7) és s(13) meddig csökkenthető?
Üdv: HK
|
|
|
| [514] Lóczi Lajos | 2004-10-08 23:29:47 |
 Úgy tűnik, rengeteg ilyen prím van. Például az első száz ilyen tulajdonságú prím az alábbi: 10000079, 10000721, 10001213, 10001461, 10001707, 10002067, 10002203, 10002589, 10003247, 10003879, 10004207, 10005431, 10005833, 10005953, 10007359, 10007537, 10007707, 10008371, 10009381, 10009871, 10010141, 10011247, 10012213, 10012351, 10012757, 10013147, 10013747, 10014341, 10014379, 10014941, 10015487, 10016693, 10016911, 10016917, 10017613, 10017809, 10020853, 10021129, 10021147, 10021723, 10022251, 10022543, 10023691, 10023901, 10024193, 10024499, 10024507, 10024909, 10025879, 10025933, 10026287, 10026901, 10027159, 10028581, 10028587, 10029049, 10029931, 10030103, 10031929, 10032053, 10032989, 10033169, 10033409, 10033571, 10033763, 10033981, 10034537, 10035169, 10035833, 10036127, 10036357, 10037207, 10037389, 10038659, 10039093, 10039273, 10039577, 10040117, 10040269, 10041749, 10042289, 10042757, 10042759, 10042883, 10043699, 10043911, 10044113, 10044313, 10045379, 10045627, 10045949, 10046807, 10047319, 10048331, 10048789, 10051367, 10052377, 10052663, 10053157, 10053301.
|
| Előzmény: [507] SAMBUCA, 2004-10-08 21:44:15 |
|
|
|
| [511] SAMBUCA | 2004-10-08 22:39:45 |
 hat igen: a,s,d,f,g,h,j,k = a,b,c,d,e,f,g,h
|
|
|
|
|
| [507] SAMBUCA | 2004-10-08 21:44:15 |
 Itt egy erdekes feladat: /just for fun/
Keressunk olyan 8jegyu abcdefgh alaku primszamot (a,s,d,f,g,h,j,k nem feltetlenul kulonbozo nemnegativ egeszek, a 0 ), hogy abcdefghabcdefgabcdefabcdeabcdabcaba 0 ), hogy abcdefghabcdefgabcdefabcdeabcdabcaba
is prim legyen!
|
|
| [506] SAMBUCA | 2004-10-08 20:58:51 |
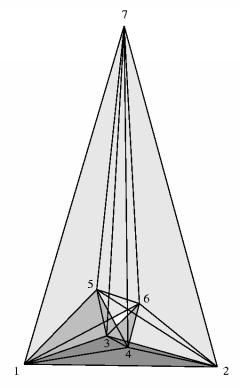
 Bocsanat. Majd elfelejtettem a legkevesebb oldallal rendelkezo szabalyos testet a tetraedert.
|
|
|
|
| [503] Hajba Károly | 2004-10-08 13:57:02 |
 Kedves Sambuca!
-Ki állította, hogy lehet?
-Ki mondta, hogy ide csak matekolimpián szerepeltek?, kiemelt matektagozatosok, szuperzsenik (mint pl. Te) írhatnak?
-Kinek van meg a Rieman?
De ha Te ennyire okos vagy, kérlek segíts! Nem kaptam még választ egy számomra megoldhatatlannak tűnő kérdésre, melyet a Geometria 27. feladatában adtam fel. Gondolom Te tudod, hol található rá válasz?
Üdv: HK
|
| Előzmény: [500] SAMBUCA, 2004-10-08 12:03:33 |
|
| [502] Moderátor | 2004-10-08 12:58:20 |
 Kedves SAMBUCA/HOMI,
Ha lehet, kicsit fogd vissza magad. Megmondhatod, hogy ez vagy az a tétel ismert, vagy neked melyik feladat (nem) érdekes és miért, de lehetőleg olyan modorban, hogy ez senkit se sértsen.
M.
|
| Előzmény: [500] SAMBUCA, 2004-10-08 12:03:33 |
|
| [501] HOMI | 2004-10-08 12:13:20 |
 Bocsi hogy csak így. De most ezek télleg érdekes feladatok? Mondok egy érdekes feladatot: 666. feladat: Adott 2n-1 egész szám. Biz. be, hogy kiválasztható közülük pontosan n úgy, hogy összegük n-nel osztható. Kellemes gondolkozást!!!!! Üdv. HOMI
|
|
|
| [499] Hajba Károly | 2004-10-08 01:05:14 |
 105. feladat:
Fel lehet-e osztani egy 60 egységnyi oldalú kockát kisebb kockákra úgy, hogy minden kisebb kocka élei különböző egész számú egységnyi hosszú legyen?
HK
|
|







 Rieman
Rieman