| [908] b.andi | 2005-05-05 12:13:12 |
 Köszi szépen!!!! Nem akarok visszélni segítőkészségeddel, de nagyon megköszönném, ha segítenél (vagy valaki más)ezekben! :)
1. Adott A(-2;1) és B(8;1). Az y tengely mely pontjaiból látszik az AB szakasz derékszög alatt?
2.Mi az egyenlete annak a körnek, melynek sugara négyzetgyök 5, és az "e": x-2y=6 egyenest A (2;4) pontjában érinti?
3. Írja fwl az (x-2)2 +(y-1)2 =5 kör y=2x egyenessel párhuzamos érintőinek egyenletét!
|
| Előzmény: [907] Fálesz Mihály, 2005-05-05 10:12:06 |
|
| [907] Fálesz Mihály | 2005-05-05 10:12:06 |
 A pont a II. síknegyedben van, a kör középpontja is ott lesz. Legyen a középpont (-a,a), a sugár a. A kör egyenlete:
(x+a)2+(y-a)2=a2.
Az egyenletnek teljesülnie kell x=-2, y=4 esetén, tehát
(-2+a)2+(4-a)2=a2
a2-12a+20=0
a=2 vagy a=10.
A két lehetséges egyenlet tehát:
(x+2)2+(y-2)2=4 és (x+10)2+(y-10)2=100.
|
| Előzmény: [906] b.andi, 2005-05-05 09:26:14 |
|
| [906] b.andi | 2005-05-05 09:26:14 |
 Hello! Megoldanátok nekem ezt a feladatot? ( csak arra vagyok kiváncsi, hogy jól dolgoztam-e): Egy kör érinti mindkét tengelyt és átmegy a P(-2;4) ponton. Mi a kör egyenlete?
|
|
| [905] Lóczi Lajos | 2005-05-04 22:34:50 |
 163. feladat. Tekintsünk egy r>0 sugarú kört egy adott perempontjához tartozó érintőegyenessel együtt. Egy teljes fordulat erejéig csúszásmentesen görgessük végig a kört az egyenesen. A kijelölt perempont eközben egy G görbét ír le. Mekkorának válasszuk r értékét, ha azt szeretnénk, hogy az egyenes és G által határolt síkidom területének és kerületének mérőszáma ugyanakkora legyen?
|
|
| [904] tudniakarok | 2005-05-04 22:18:53 |
 Na ehhez a következőt találtam:
"... július 27-ére minden adat végleges lesz ahhoz, hogy beindíthassuk a vonalhúzás számítógépes eljárását. Ez egy többszörös biztosítással lefuttatott matematikai algoritmus,mely folyamatosan összeveti az egyes intézmények és szakok irányszámait az oda jelentkezők számával és elért felvételi pontszámaival. Minden egyes szak esetében az oda jelentkezők pontszámaiból alakul ki egy sorrend,amelynek csúcsán a legtöbb pontot elért jelentkező áll, majd sorra következik a többi... a szabály az, hogy a ténylegesen felvett hallgatók száma alulról közelíti meg az irányszámot. Mindezek figyelembevételével alakul ki végül július 27-én, előreláthatólag késő este a ponthatár..."
|
| Előzmény: [897] Csimby, 2005-04-29 19:15:31 |
|
| [903] Lóczi Lajos | 2005-05-04 22:09:28 |
 Következzék egy régi feladat:
162. feladat. Tekintsünk két kört, K1-et és K2-t, sugaraik legyenek rendre 1, illetve r egység. K2 középpontja K1 peremén helyezkedik el. Mekkorának válasszuk r értékét, hogy a két körlap metszetének területe K1 területének fele legyen?
|
|
| [902] Atosz | 2005-05-04 17:53:49 |
 Sziasztok!
Kissé eltűntem az utóbbi időben, de újra itt vagyok, s gondolom ilyenkor illik egy új feladattal visszatérni. Nem túl nehéz.
[161]. feladat
A távoli hegyi faluban akkor tartanak ünnepet, amikor a kolostor és a templom harangjai pontosan egyszerre konganak. Mindkét harangot szabályos időközönként, egész számú percenként kongatják; de természetesen más ritmusban. Ma a harangok déli 12-kor fognak együtt kongani. Az ünnepnapok között a harangok felváltva konganak, és előfordul, hogy a nem ünnepnapok egyikén csak egy percnyi eltérés választja el a két hangot. Legutóbb a harangszók egybeesése déli 12 órakor történt, az azóta eltelt napok száma prímszám.
Hány napja történt ez?
Jó fejtörést hozzá!
|
|
|
| [900] BohnerGéza | 2005-05-03 12:49:15 |
 Kedves Csimby!
Sajnos az asztroidra vonatkozó feltevésed nem jó. Kiszámoltam, egységnyi sugarú körben az asztroid hossza 6, a kör kerülete 2*PI.
(A számolás egy egyszerű integráláshoz vezet.)
|
| Előzmény: [884] Csimby, 2005-04-26 22:06:56 |
|
|
| [898] levi | 2005-04-29 21:47:06 |
 Nagyon érdekelne hogy hogyan lehet eljutni ahhoz a kitevőhöz (szóval tulajdonképpen a megoldás érdekelne)... persze csak ha el lehet árulni...
|
|
| [897] Csimby | 2005-04-29 19:15:31 |
 Más kérdés:
Tudja valaki, hogyan határozzák meg a felvételi ponthatárokat, milyen algoritmussal? (Ez ugyanis csöppet sem tűnik egyértelműnek)
|
|
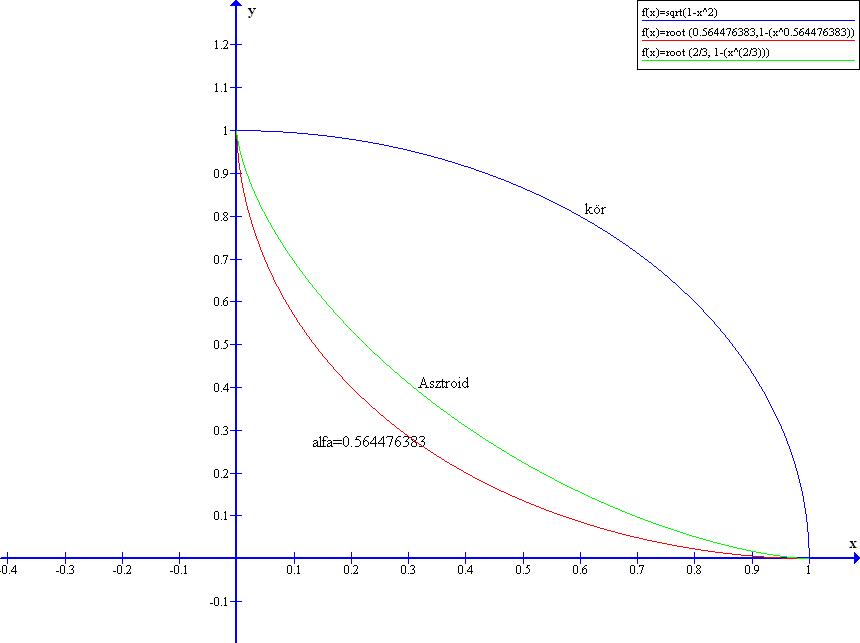
| [896] Lóczi Lajos | 2005-04-29 17:05:01 |
 Igen, csak véletlen.
A keresett kitevő ugyanis megközelítőleg  =0.561493300750... (melyhez tartozó =0.561493300750... (melyhez tartozó 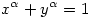 -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.) -alakzat kerülete az egységkör kerületétől csak kb. 10-12-nel tér el.)
|
| Előzmény: [895] Csimby, 2005-04-29 16:42:04 |
|
|
|
|
|
|
|
|
|
|
|
| [884] Csimby | 2005-04-26 22:06:56 |
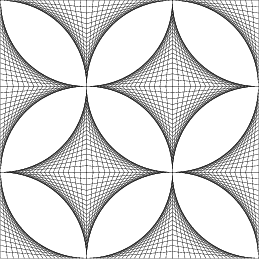
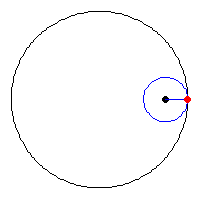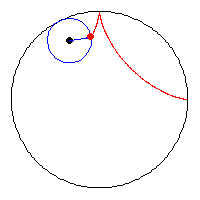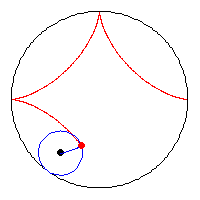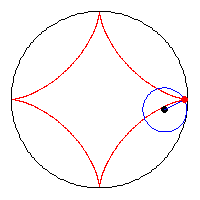
 A kis kör sugara a nagy kör sugarának a negyede, az animációból látszik, hogy az asztroid és a nagy kör kerülete megegyezik. (egy negyed körív = egy negyed asztroid ív = a kis kör teljes kerülete)
|
 |
| Előzmény: [883] Csimby, 2005-04-26 22:02:49 |
|
|







 <1 kitevőt (pl. ügyes programokkal), melyre a
<1 kitevőt (pl. ügyes programokkal), melyre a 
 a kerülete, és a o,1 zárt intervallumban lévő ívét vizsgáltam. Ennek az egyenlete (x-1)2+(y-1)2=1 (0
a kerülete, és a o,1 zárt intervallumban lévő ívét vizsgáltam. Ennek az egyenlete (x-1)2+(y-1)2=1 (0 x,y
x,y