| [933] levi | 2005-05-10 13:52:19 |
 nem tud vki vmi olyan könyvet/bármit ami a 4,5,...dimenziós geometriával foglalkozik? elkezdett érdekelni a dolog, gondoltam itt biztos tud vki vmi ilyet ajánlani...
|
|
|
|
| [930] neo | 2005-05-10 01:07:15 |
 Http://matek2005.fw.hu
|
|
| [929] Lóczi Lajos | 2005-05-10 00:23:57 |
 Gratulálok, nekem is ezek az értékek jöttek ki (bár én sehol sem használtam geometriai meggondolásokat -- vannak példák arra, hogy az analógiáink magas dimenzióban nem működnek), úgyhogy azért a többieknek is maradhat még annyi a feladatból, hogy vagy igazoljuk a geometriai érvelésedet, vagy geometriától függetlenül oldjuk meg a problémát.
|
| Előzmény: [928] levi, 2005-05-09 23:50:42 |
|
| [928] levi | 2005-05-09 23:50:42 |
 167-170. feladatra: a két dimenziós eset vizsgálata: vegyük a két külső kör középpontját, ezek A(r+1,0) és B(0,r+1). Vegyük azt a szakaszt amit ez a két pont határoz meg, a keresett legkisebb sugarú kör érinti egymást, mégpedig a szakasz felezőpontjában, így már adott ennek is a koordinátája, a sugár egyenlő a felezőpont és az egyik külső kör középpontjának távolságával, r-re rendezés után szerintem ez: 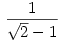 . .
Három dimenziós esetben kössük ismét össze ezeket a pontokat, ezek egy háromszöget fognak meghatározni. a keresett pont a háromszög magasságpontja. a háromszög szerencsére szabályos, így a magasságpont egybeesik a súlyponttal, a súlypont koordinátái pedig kiszámíthatóak a csúcsok koordinátáiból... ismét felírva egy középpont és a magasságpont távolságát az egyenlő lesz r-rel , és utána rendezve megkapjuk r-t, ami nálam 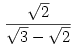
ezután az általános n dimenziós eset: sajnos nem tudok 4 vagy magasabb dimenzóban látni, és annak a (koordináta)geometriáját sem tudom, de talán az előző két esetből levont következtetésem jó lesz... szóval a körök középpontjai adottak, a keresett pont mely egyenlő távolságra van mindegyiktől szerintem K(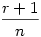 , , 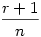 ,..., ,...,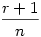 ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól ) (összesen n-szer). Ekkor egy középpont és a K távolsága lesz egyenlő a sugárral. Mivel a középpontok mind egy-egy tengelyen vannak, ezért koordinátái közül pontosan egy lesz r+1 az összes többi 0. Ha felírjuk a távolságképletet, majd kiemelünk a gyök alól 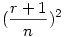 -t, akkor azt kapjuk hogy -t, akkor azt kapjuk hogy 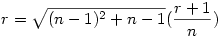 . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy . Rendezzük r-re, majd egyszerűsítünk, akkor azt kapjuk hogy 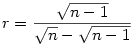 . Ezalapján az n=4 eset már könnyen kiszámolható... . Ezalapján az n=4 eset már könnyen kiszámolható...
|
|
|
|
| [925] Lóczi Lajos | 2005-05-09 21:58:25 |
 169. feladat. Tekintsük a 4 dimenziós térben az origó középpontú egységsugarú hipergömböt (azaz 4 dimenziós gömböt). A 4 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 4 darab egyforma, r sugarú hipergömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 4 hipergömbön rajta van?
170. feladat. Általánosítsuk az előző kérdést n-dimenzióra, és adjuk is meg a minimális r>0 értéket a dimenzió függvényében.
|
|
| [924] Lóczi Lajos | 2005-05-09 21:55:48 |
 168. feladat. Tekintsük a közönséges 3 dimenziós térben az origó középpontú egységgömböt. A 3 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 3 darab egyforma, r sugarú gömböt. Legalább mekkora legyen az r>0 szám értéke, hogy legyen olyan pont, amely mind a 3 gömbön rajta van?
|
|
| [923] Lóczi Lajos | 2005-05-09 21:52:11 |
 167. feladat. Tekintsük a közönséges 2 dimenziós síkon az origó középpontú egységkört. A 2 koordinátatengely pozitív félegyenesén az origótól 1+r távolságra helyezzünk el 2 darab egyforma, r sugarú kört. Legalább mekkora legyen az r>0 szám értéke, hogy e két külső körnek is legyen közös pontja?
|
|
|
|
|
|
|
| [917] Lóczi Lajos | 2005-05-05 23:16:27 |
 165. feladat. Legyen f az egész számegyenesen értelmezett, legalább kétszer deriválható korlátos valós függvény. Igaz-e, hogy f második deriváltjának van legalább egy valós zérushelye?
|
|
| [916] b.andi | 2005-05-05 22:47:36 |
 Jó én se szó szoros értelemben értettem a gúnyolódást ez inkább önirónia volt... Tudod azért teszem a röhögőfejeket a mondataim után, hogy azt nem kell halálosan komolyan venni...Amúgy tényleg köszi a segítséget!!!
|
| Előzmény: [914] jonas, 2005-05-05 20:37:50 |
|
| [915] Lóczi Lajos | 2005-05-05 22:42:01 |
 164. feladat. Számítsuk ki a
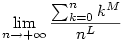
határértéket, ha M és L adott pozitív egészek.
|
|
|
| [913] b.andi | 2005-05-05 19:35:27 |
 Most kigúnyolsz? Ne máááááá..... :) mondtam hogy nem vagyok matek zseni, nekem már ez is érdekes, ha egyátalán nekifogok egy ilyen feladatnak... :) Vagy ha tudsz egy olyan topicot, hogy "Oldjatok meg gagyi feladatokat" akkor szólj :) Na mindegy amúgy nagyon nagyon köszi!!!!!! most jut eszembe nem is az volt a kérdés, hogy rajta van-e, hanem hogy mi a kör egyenlete... Nekem ez lett k:(x-3)2 + (y+4)2= 5 (vagyis négyzetgyök öt a négyzeten) (ti hogy tudtok felső indexbe írni?) és k': (x-1)2 + (y-6)2 =5 Szerintetek ez jó?
|
| Előzmény: [912] jonas, 2005-05-05 18:24:33 |
|
|
| [911] Sirpi | 2005-05-05 15:25:54 |
 Az 1. feladatot bevállalom, a többit meghagyom másoknak.
A(-2;1), B(8;1), P(0,y), ahol y az ismeretlen. Innen a PA vektor (-2; 1-y), a PB vektor (8; 1-y)
Két vektor meröleges, ha skalárszorzatuk nulla, azaz -16+(1-y)2=0, innen y=5 vagy y=-3.
|
| Előzmény: [908] b.andi, 2005-05-05 12:13:12 |
|
| [910] b.andi | 2005-05-05 15:02:07 |
 Nem adok többet ígérem!!!! :) Az előzőt rosszul csináltam mert nem a II. síknegyedbe "raktam" a pontot. Még ezenkívül a kettesbe mertem belekezdeni, végig is csináltam, de hát nem vagyok egy matek zseni... a többiről fogalmam sincs (hát a matektanárunk nem egy ász):) Egyébként ezek voltak a matek dolgozatom kérdései...
|
|
|





 . A kerület 8r + 2r
. A kerület 8r + 2r
