| [360] Hajba Károly | 2004-05-24 01:09:41 |
 Kedves Csimby!
Én eddig 3-at találtam: a0=1;a1=1;a12=144. Az Excell 15 jegy pontosságával a73=806.515.533.049.393-ig nincs újabb. Efölött az Excell már alkalmatlan, programozói gyakorlatom nincs, hogy írjak egy rövid rutint, s általam nem ismert egy Fib(n)=... közvetlen képlet, melyből esetleg lehetne következtetni valamit.
Kiváncsi vagyok a Te megoldásodra is.
HK
|
| Előzmény: [359] Csimby, 2004-05-23 22:59:42 |
|
| [359] Csimby | 2004-05-23 22:59:42 |
 80.feladat Hány négyzetszám van a Fibonacci-sorozatban?
|
|
|
| [357] Kós Géza | 2004-05-17 14:11:17 |
 Mielőtt az Emberevők Szigete végleg elsülyedne a Feledés Tengerében, próbáljuk meg Csimby gondolatait egy teljes megoldássá rendezni.
Az előzést úgy értettem, hogy két falu között az egyik megelőzi a másikat. Tehát U elindul U-ból, és miközben V felé bandukol, megelőzi őt vetélytársa, a konkurrens felekezet tanait terjesztő T is, és V is partra száll V-ben. Mire U odaér V-be, addigra ott már megették T-t, és U mit sem sejtve tovább mehet W-be, ahol ő lesz a menü. Az U tehát U-ból indul, W-ben végzi, és közben mégis elindult valaki V-ből...
Szeretném hangsúlyozni, hogy az előzés lehetőségét példának hoztam fel arra, hogy sok részlet nincs következetesen és pontosan leírva. A teljesen végig nem gondolt részletekben pedig elbújhat egy olyan hiba, ami az egész megoldást megfúrja.
* * *
Térjünk vissza a megoldásra. Osszuk a misszionáriusokat két csoportra. Az egyikbe tartoznak a szerencsétlenebbek, akiket azonnal megesznek. A másik csoport a még szerencsétlenebbek, akiknek előbb dolgozni is kell; az a falu, ahonnan indulnak, az odaérkezésükkor éppen pogány. Minden még szerencsétlenebb misszionárius (MSZM) megtesz egy bizonyos utat a parton.
Csimby megoldása a következő lépésekből állna:
1. Az MSZM-ek által megtett utak nem fedhetik át egymást; nincs olyan partszakasz, ahol két misszionárius is áthaladt;
2. Az MSZM-ek által megtett partszakaszok egymáshoz csatlakoznak és a sziget teljes kerületét pontosan egszer lefedik.
3. Minden egyes faluban összesen két misszionárius fordult meg, és végül a falu újra pogány lett.
|
| Előzmény: [342] Csimby, 2004-04-23 14:09:11 |
|
| [356] joe | 2004-05-15 19:16:15 |
 A 78. feladathoz hasonló, de talán egy kicsit érdekesebb és elegánsabb megoldású a következő:
79. feladat: Tetszőleges n természetes számra állítsuk össze az A és B betűkből az összes lehetséges n betű hosszúságú szót. Osszuk e szavakat két halmazba, Pn-be és Nn-be aszerint, hogy egy adott szóban a BA betűcsoport előfordulásainak száma páros vagy páratlan (a nullát páros számnak tekintjük). Például a BABBBBA szó és az AAAAAAB szó a P7 halmazba, az AABBABB szó és a BABAABA szó az N7 halmazba tartozik. Határozzuk meg, mely n számokra van a Pn és az Nn halmaznak ugyanannyi eleme.
Hogy őszinte legyek, a 78. feladat megoldása nem túl szép, a 79.-re azonban ismerek egy ritka érdekes bizonyítást, ami eltér a "hivatalos" megoldástól és szerintem sokkal szebb.
Ha valaki tudna valamit mondani az ilyen feladatok eredetéről és mélyebb jelentőségéről, azt megköszönném.
|
|
| [355] joe | 2004-05-14 18:49:38 |
 Mint új fórumos, egy feladattal kezdeném:
78. feladat: Tetszőleges n természetes számra állítsuk össze az A és a B betűkből az összes lehetséges n betű hosszúságú "szót". Jelölje pn azon n hosszúságú "szavak" számát, melyek nem tartalmaznak sem négy egymást követő A betűt (AAAA csoportot), sem három egymást követő B betűt (BBB csoportot). Határozzuk meg a következő kifejezés értékét
|
 |
|
| [354] skg | 2004-05-13 19:49:14 |
 Hi!
Régebben beszéltetek itt a bűvös kockáról (rubik) azt szeretném megkérdezni, hogy tudtok-e olyan lapot, ahol van valami róla?
|
|
|
|
|
|
|
| [348] nadorp | 2004-04-27 15:42:14 |
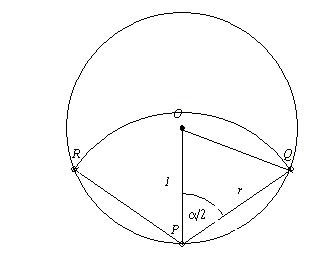
 Megoldás a 77. feladatra.
Legyen legelő középppontja O, sugara 1. A karó helye legyen P, a kötél hossza r ( lásd az ábrát). A P középpontú r sugarú kör messe a legelőt a Q és R pontokban.
Legyen RPQ = = . Nyilván . Nyilván  tompaszög, hiszen ellenkező esetben a két körív közti terület nagyobb a legelő felénél és az is látszik, hogy tompaszög, hiszen ellenkező esetben a két körív közti terület nagyobb a legelő felénél és az is látszik, hogy 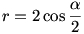 . A két körív közti terület egy körcikkre és két egybevágó körszeletre bontható, a területre: . A két körív közti terület egy körcikkre és két egybevágó körszeletre bontható, a területre:
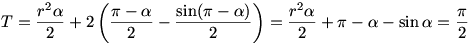
Mivel 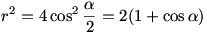 , ezért , ezért
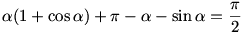
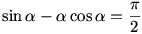
Ezt az egyenletet csak közelítőleg lehet megoldani,  =109,19o körül van.Innen r=1,16 egység. =109,19o körül van.Innen r=1,16 egység.
|
 |
|
| [347] lorantfy | 2004-04-27 12:33:01 |
 Az 59. feladat így szólt: Oldjuk meg a
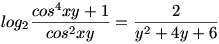
egyenletet, ha (x,y) R2 ! R2 !
Az 59. feladat megoldása: A logaritmus „hasában” álló A kifejezés:
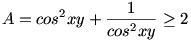
így log2A 1. 1.
A jobb oldali B tört nevezője: y2+4y+6=(y+2)2+2 2, így B 2, így B 1. 1.
A két oldal csak akkor lehet egyenlő, ha log2A=B=1. tehát y = -2. A = 2-ből cos2xy=1. cos2(-2x)=cos2(2x)=1, amiből cos2x=1 vagy cos2x=-1, 2x=k . .
Tehát 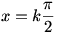 , ahol k , ahol k Z. Z.
|
| Előzmény: [343] Hajba Károly, 2004-04-27 00:15:48 |
|
|
|
| [344] lorantfy | 2004-04-27 10:47:14 |
 A 63. feladat ez volt: Három barátnő főzéshez készül, az egyik 5 db fát, a másik 3 db fát hozzott a spórba és így mindhármójuk megfőzött. A harmadik, mivel nem volt tüzifája, 8 forinttal járult hozzá a tüzifa költségekhez. A másik két barátnő milyen arányban osztozik igazságosan a pénzen?
A 63. feladat megoldása: A harmadik barátnő 8 Ft-ot ad a rá eső 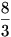 fahasábért, így fahasábért, így 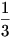 fahasáb 1 Ft-ot ér. fahasáb 1 Ft-ot ér.
Az első barátnő, aki 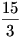 fahasábot adott fahasábot adott 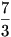 -al adott többet mint a saját része, így 7 Ft-ot kap, míg a második, aki -al adott többet mint a saját része, így 7 Ft-ot kap, míg a második, aki 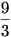 -ot adott csak -ot adott csak 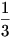 -al adott többet mint a saját része, tehát 1 Ft-ot kap a 8 Ft-ból. -al adott többet mint a saját része, tehát 1 Ft-ot kap a 8 Ft-ból.
|
| Előzmény: [343] Hajba Károly, 2004-04-27 00:15:48 |
|
| [343] Hajba Károly | 2004-04-27 00:15:48 |
 Kedveseim!
Az alábbi feladatok még megoldóra várnak. Kellemes töprendést!
HK
|
 |
|
| [342] Csimby | 2004-04-23 14:09:11 |
 Kedves Géza, Onogur és Mindenki aki veszi a fáradságot, hogy nyomonkövesse a szigetes feladat megoldását!
Azért nem írok (legalábbis egyenlőre) olyan hozzászólást amiben minden benne van, mert vki úgyis beleköt (ez persze nem baj) és akkor írhatnám újra az egészet. Egyenlőre tehát a legutóbb feltett kérdésekre válszolok:
I. Esetleg valaki meg is előzhette a-t? A hittérítők sorban haladnak, nem hagyhatnak ki falut és egy faluban egyszerre csak egy hittérítő tartózkodhat, tehát nincsen előzés.
II. Ha az a-ból induló misszionárius b-ben végzi, miért ne indulhatott volna közben más pap a kettő között? [326] hozzászólás: "ha lettek volna innen induló papok, akkor a pap meghalt volna az a faluhoz legözelebbi ilyen indulási faluban" (legyen ez a falu y ) Bővebben: Az a és b falu között indulók közül y az a-hoz legközelebbi indulásipont, tehát az a és b között indulók közül csak y járhatott y-ban. Mivel feltettük, hogy időben a az első hittérítő, és I.szerint nicsen előzés, ezért nem lehetséges az sem, hogy valaki a falu előttről indult és így jutott el az a utáni falutól y-ig tartó partszakszra. Tehát a-tól y-ig még senki sem járt egy faluban sem, y-ban pedig egy ember járt, vagyis ha lenne ilyen y falu, akkor a pap y-ban halt volna meg és nem b-ben. Ami ellentmondás! Ebből az is következik, hogy az a-tól a halálozási falujáig, (b-ig) terjedő partszakaszon a-n kívül senki sem indult időben b előtt.
Ha a b-ből induló misszionárius c-ben végzi, nem indulhatott volna közben más pap a kettő között, mert: ha lettek volna innen induló papok, akkor b pap meghalt volna a b faluhoz legözelebbi ilyen indulási faluban. (legyen ez a falu z ) Bővebben: A b és c falu között indulók közül z a b-hez legközelebbi indulásipont, tehát a b és c között indulók közül csak z járhatott z-ben. Mivel az a-tól b-ig terjedő partszakaszon a-n kívül senki sem indult időben b előtt, és I.szerint nicsen előzés, ezért nem lehetséges az sem, hogy valaki b falu előttről indult és így jutott el a b utáni falutól z-ig tartó partszakszra. Tehát b-től z-ig még senki sem járt egy faluban sem, z-ben pedig egy ember járt, vagyis ha lenne ilyem z falu, akkor b pap z-ben halt volna meg és nem c-ben. Ami ellentmondás! Ebből az is következik, hogy a b-től b halálozási falujáig, (c-ig) terjedő partszakaszon b-n kívül senki sem indult időben c előtt.
Bármely két falura bizonyítható az állítás ugyanezzel a gondolatmenettel ...
III. Ha az x-edik faluba megérkezik a majd b , akkor x=a vagy x=b? Azt feltettem, hogy a és b az első két ember aki x-ben jár, tehát a és b közül a második aki oda ér biztosan meghal (legyen ez b). De II. szerint b és a között nem indulhatott senki, tehát a-nak x-ből kellett indulnia.
Csimby
|
|
| [341] Hajba Károly | 2004-04-22 20:08:44 |
 77. feladat: (Felesben legel e kecske)
Egy kecskepásztor egyik nap egy kerek legelőre vitte ki egyetlen kecskéjét legelni. De hogy ne kelljen másnap újabb legelő után nézni, úgy szeretné kikötni, hogy csak a legelő felét tudja a kecskéje lelegelni. A karót a legelő szélén verte le. Milyen hosszúra kell a kecske kötelékét engednie?
HK
|
|
| [340] Kós Géza | 2004-04-22 16:52:21 |
 Kedves Csimby,
Ha nem veszed zokon, még egy kicsit megdolgoztatlak. A túrórudi csak teljes megoldásért jár, amin nem fog semmilyen javítói kötekedés. :-)
Egy KöMaL-javító szinte minden mondat végén odaírná pirossal, hogy "Miért?". Például miért igaz, hogy ha az x-edik faluba megérkezik a majd b, akkor x=a vagy x=b? Ha az a-ból induló misszionárius b-ben végzi, miért ne indulhatott volna közben más pap a kettő között? (Esetleg valaki meg is előzhette a-t...)
Mindez persze csak akadékoskodás, de azért nem értelmetlen. Egy teljes megoldásban nem lehetnek ilyen homályos pontok, mert ezek hibák forrásai lehetnek. Én úgy látom, hogy közel vagy a megoldáshoz, sok mindent látsz, amin múlik, de a megoldás pontos leírása még mindig hiányzik. (Jó lenne az elejétől a végéig leírni, nem olyan hosszú, és könnyebb elolvasni, ha nem hivatkozik korábi hozzászólásokra.)
Géza
|
| Előzmény: [339] Csimby, 2004-04-22 00:20:43 |
|
| [339] Csimby | 2004-04-22 00:20:43 |
 Kedves Onogur!
Legyen x olyan falu ahol 2-nél többen is megfordultak. Legyen az első két ember aki járt x-ben a és b. Ekkor x=a vagy x=b, legyen most x=a. Tehát b pap a faluban halt meg. Vagyis a és b azon papok csoportjába tartozik, akiket [326]-os hozzászólásomban a megoldás elején felsoroltam. De az ebbe a csoportba tartozó papok "váltják" egymást (onnan következik egy új ahol a régi meghalt) vagyis elképzelhetetlen, hogy egy harmadik c pap is átmenjen x-en (ha c is a papoknak ebbe a csoportjába tartozik), mert az ebbe a csoportba tartozó papok útvonalai pontosan lefedik a partot és nincs olyan szakasz amin két pap járt volna. A másik csoportba tartozó papok sem mehetnek át x-en, mert x-ből nem indulhatnak (hiszen onnan már a indult) és ők az induló falujukban meghalnak.
|
| Előzmény: [338] Hajba Károly, 2004-04-21 22:15:25 |
|
| [338] Hajba Károly | 2004-04-21 22:15:25 |
 Kedves Csimby!
A feladat szép és elegáns befejezéséhez azt kellene kizárni, hogy semmi szín alatt nem jöhet egy faluba 2-nél több térítő. (Természetesen nem lehet ilyen ellenpéldát mutatni, de bizonyítani igen.)
HK
|
| Előzmény: [337] Csimby, 2004-04-21 15:39:02 |
|
| [337] Csimby | 2004-04-21 15:39:02 |
 Tehát ha jó az amiket leírtam, akkor mindegyik faluba pontosan 2 pap érkezik (összesen). Ez egy kicsit meglepő, de most hirtelenjében nem találok ellenpéldát...
|
| Előzmény: [336] Csimby, 2004-04-21 15:15:13 |
|
| [336] Csimby | 2004-04-21 15:15:13 |
 Kedves Onugor!
A térítőket két csoportra oszthatjuk: Akik beleférnek a megoldásom elején adott felsorolásba és akik nem. A két csoport közül melyiknél gondolod, hogy fenn állhat ez a problema? (én úgy gondolom, egyikben sem)
|
| Előzmény: [335] Hajba Károly, 2004-04-21 13:49:04 |
|











 =
= . Nyilván
. Nyilván 
 R2 !
R2 !  1.
1.  1.
1.  .
. 