| [110] Maga Péter | 2012-07-16 16:41:04 |
 Egyébként tényleg megválaszolandó kérdés, mi a nagyon gyenge szereplés oka. Néhány indító észrevétel.
A hat versenyzőnk közül csak három küldte az A-t, és olyan is van, akinek a nevét egyik pontversenyben sem találom. Általában véve is nagyon kevesen vesznek részt az A pontversenyben. Idén hallottam először, hogy 'az olimpiai feladatok inkább B szintű feladatokhoz hasonlítanak' (éppen arra való buzdításként, hogy az olimpiai aspiránsok is küldjék a B-t). Ha ebben van is igazság, a nehezebb olimpiai példákhoz már mindenképpen kell nehéz feladatokkal dolgozni. Mélyebb érvek helyett: ha a citált buzdítást az olimpikonok komolyan vették, akkor meg kell nézni, hogy a 3., 5., 6. (hagyományosan is nehéz) feladatokra nem született jó magyar megoldás, összesen is csak 9 pontot kapargattak össze versenyzőink. [Tavaly sem oldotta meg senki a 3. és a 6. feladatot, az 5. ugyan jól alakult, de akkor a 2. feladaton betliztünk - bár akkor az kivételesen nehéz 2. feladat volt.]
A 4. feladat függvényegyenlet volt, amiben nem szoktunk erősek lenni, annak ellenére sem, hogy a csapat felkészítésének általában része egy kis fejtágító függvényegyenletekről. A függvényegyenletek kimaradnak a magyar tananyagból, versenyeken elvétve van egy-egy ilyen feladat, ebben sokkal gyengébbek a magyar diákok, mint sok más témakörben (talán éppen ezért is van a fejtágító, de ez persze minden igyekezet ellenére sem pótolhatja a megoldott feladatok tömegét).
Egy további probléma, hogy borzasztóan rosszul kommunikálják a diákok a gondolataikat (az olvasó nem érti 'Mit tudunk? Mit szeretnénk? Mit állítunk? Mit fogunk most bizonyítani? Miért elég ez?'). Nem tudom, hogy magyar sajátosság-e, de nálunk a tendencia elborzasztó. (Nyilván egy olimpián a fordításnál ezt megpróbálják leplezni, DE) lehet, hogy a gondolatok zavaros közlése egy idő után maguknak a gondolatoknak a zavarosságát is okozza (amikor már befelé is zavarosan fogalmazódik meg, és már a diák sem érti 'Mit tudunk? Mit szeretnénk? Mit állítunk? Mit fogunk most bizonyítani? Miért elég ez?'). És ez már egy könnyebb IMO-feladat esetében is jóvátehetetlen vétség.
|
|
|
| [108] Róbert Gida | 2012-07-16 16:14:19 |
 "kizárt, hogy vidéki, nem specmatekos iskolából, hátszél nélkül kijusson az olimpiára."
Hetyei Gábor kijutott Máté iskolájából, igaz 1983-ban. Egyébként 1963-1994 között az indulók 30
"Mivel nem specmatekos, ezért nehezebb összehasonlítani az eredményeket, "
Ezért is valószínűleg nem nézik ezeket az eredményeket. Továbbá szerintem a válogatókon írt dolgozatok nagyobb súllyal számítanak.
"MEMO: az érthetőség kedvéért. A tavalyi MEMO-n két olyan ország csapata is mögöttünk végzett, aki idén megelőzőtt bennünket. Vagy ők javultak fel, vagy mi lettünk gyengébbek. Mind a kettő a magyar oktatás, kiválasztás szégyene."
Vagy csak nem nekünk kedveztek a feladatok típusai, ahogy más fórumon is írták. Tényleg van egy hanyatlás 2000-es évektől kezdve, ennek egy kisebb része azzal magyarázható, hogy több ország indul, manapság cirka 100. Egy másik ok lehet, hogy egyre kevesebb gyerek születik, egyre kisebb létszámú a 17-18 éves korosztály..
|
| Előzmény: [106] gyarmatii, 2012-07-16 15:02:47 |
|
| [107] Maga Péter | 2012-07-16 16:01:27 |
 Abban az évben, amikor én tartalék lettem, volt egy vidéki, nem specmatos olimpikon (aki egyéb érdemei mellett valószínűleg a Kürschák-győzelmével váltotta meg az athéni repjegyét). Az említett bennfentes állítását megdöntő ellenpéldát valószínűleg más évjáratokban is lehet találni.
Nagyon sokat számít az olimpiai szakkörön történő részvétel és az ottani aktív szereplés. Ez semmiképpen sem nevezhető szubjektív szempontnak, még akkor sem, ha nem is tudjuk a versenyeredmények skáláján mérni.
A gyenge eredményhez szerintem a válogatásnak nem sok köze van. Korábban is ez volt a rendszer, és nagyon erős csapatokat is hozott össze.
---
Fel a fejjel! Ha például valamelyik neves amerikai egyetemen szeretett volna ösztöndíjat kapni, most rögtön, a középiskola után, akkor abban persze sokat segített volna neki egy IMO-kerettagság. De a későbbiekben más szempontok kerülnek előtérbe. A csapatból való kimaradás legrosszabb következménye az lehet, ha nehezen emészti meg.
|
| Előzmény: [106] gyarmatii, 2012-07-16 15:02:47 |
|
| [106] gyarmatii | 2012-07-16 15:02:47 |
 Mátét 11 éve visszük, küldjük versenyre. Mindig is szeretett volna eljutni az olimpiára, és ennek mindent alárendelt. 4 éve egy bennfentes azt mondta, hogy kizárt, hogy vidéki, nem specmatekos iskolából, hátszél nélkül kijusson az olimpiára. Igaza lett. A válogatási elvek: Az év elején elhangzott Pelikán úrtól, hogy a KÖMÁL pontversenyben való részvételt minden leendő olimpikontól elvárja. Ezenkívül a nívósabb versenyek eredményei (MEMO, Kürschák, OKTV-k, válogatók fognak számítani.) Máté eredményei: MEMO: ezüstérem, Kürschák: oklevél, OKTV: 1. és 4., Surányi J(1.válogató): J.A és Á.T mögött 3., KÖMAL A: 5., KÖMAL B:5. Mivel nem specmatekos, ezért nehezebb összehasonlítani az eredményeket, de több versenyen is, ahol együtt indultak, jobb helyezést el, mint az utazók többsége. Emellett még volt 2 Arany D. első helye, és 2012 Nemzetközi Magyar MV is 1. díjas volt (Itt részt vesznek Fazekasosok is). Ha reális pontszámításos válogató lett volna, akkor a 3. 4. helyen állt volna. Idén viszont nem csak az eredmények döntöttek, hanem szubjektív megitélés alapján jelölték ki az utazókat. Az eredmény ismert. Már a tavalyi 25. hely is az addigi leggyengébb szereplés volt, csak a nemFazekasosok jó eredménye mentette meg a csapatot. Az idei 38-41. hely magáért beszél. Most nem lehet azt mondani, hogy a vidéki nemspecmatekosok húzták le a teljesítményt. Elkéne fogadni, hogy a Fazekason túl is van élet, vannak olyan tehetséges tanulók, akik nem engedtek a csábításanek és nem mentek el a Fazekasba. Úgy gondolom, hogy az olimpia nem a Fazekasosok magán versenye kell, hogy legyen, hanem itt a korosztály legjobbjait kellett volna nevezni. Remélem, hogy az idei eredmény felébreszti az illetékeseket.
MEMO: az érthetőség kedvéért. A tavalyi MEMO-n két olyan ország csapata is mögöttünk végzett, aki idén megelőzőtt bennünket. Vagy ők javultak fel, vagy mi lettünk gyengébbek. Mind a kettő a magyar oktatás, kiválasztás szégyene.
|
| Előzmény: [105] Róbert Gida, 2012-07-16 14:01:11 |
|
| [105] Róbert Gida | 2012-07-16 14:01:11 |
 "Sajnos a válogatási elvekből kifolyólag előre borítékolni lehetett az eredményt."
Miért mi a válogatási elv? Több körös válogatás volt régebben és a legjobb 6 került ki. Máté indult a válogatókon?
"A tavalyi MEMO-n a mostani 6 diákból 3 ott volt, mellettük még 3 vidéki. Akkor több ponttal megelőzték a német és horvát csapatot, akik szinte ugyanazzal a csapattal most jóval előrébb végeztek."
Kérdés, hogy Janzer Olivérrel mit kezdjünk, mint a legjobb magyar olimpikonnal, aki nem MEMO tag. A 3 MEMO versenyző összehozott 47 pontot, a 3 nem MEMO tag 46-ot. Nem szignifikáns a különbség.
"Az 1-es és a 4-es feladat könnyű volt, minimum 14 ponttal kellett volna mindekinek indítania."
Akkor a negyediket miért nem minden MEMO tag oldotta meg? A második feladat megoldása konkrétan 1 sor, számtani-mértanival.
|
| Előzmény: [103] gyarmatii, 2012-07-16 08:47:09 |
|
| [104] RMG | 2012-07-16 13:54:43 |
 Az Art of Problem Solving honlapon (Results of the IMO 2012 Argentina/Final Results címen) olvasható az alábbi, kubai zászlóval ellátott hozzászólás:
"A surprise on the negative side might perhaps be the performance of Hungary. They used to be a top country, but fell out of the top-10 in the last decade. Last year they only reached rank 25, and this year they even went to rank 38. I am wondering about the reasons for this."
Úgy látszik, másokat is izgat a kérdés.
|
|
| [103] gyarmatii | 2012-07-16 08:47:09 |
 Matematikaverseny volt vagy fazekasos kirándulás? Az eddigi leggyengébb eredmény, amit elért magyar csapat. Sajnos a válogatási elvekből kifolyólag előre borítékolni lehetett az eredményt. A tavalyi MEMO-n a mostani 6 diákból 3 ott volt, mellettük még 3 vidéki. Akkor több ponttal megelőzték a német és horvát csapatot, akik szinte ugyanazzal a csapattal most jóval előrébb végeztek. Az 1-es és a 4-es feladat könnyű volt, minimum 14 ponttal kellett volna mindekinek indítania. Úgy tűnik valamit nagyon elszúrtak a Fazekasban?!
|
|
|
| [101] Róbert Gida | 2012-07-15 20:42:02 |
 Hm, az imo honlapja nem elérhető, gondolom kínai hekkerek műve.
|
|
|
|
| [98] Kós Géza | 2012-07-15 17:04:24 |
 Íme az eredmény...
|
1 |
2 |
3 |
4 |
5 |
6 |
összesen |
díj |
| Ágoston Tamás |
7 |
7 |
0 |
7 |
1 |
0 |
22 |
ezüstérem |
| Janzer Olivér |
7 |
7 |
3 |
7 |
1 |
2 |
27 |
ezüstérem |
| Nagy Róbert |
7 |
1 |
0 |
6 |
0 |
0 |
14 |
bronzérem |
| Ódor Gergely |
7 |
1 |
0 |
3 |
0 |
0 |
11 |
dicséret |
| Sándor András |
7 |
1 |
0 |
0 |
0 |
0 |
8 |
dicséret |
| Strenner Péter |
7 |
0 |
0 |
2 |
0 |
2 |
11 |
dicséret |
| Összesen: |
42 |
17 |
3 |
25 |
2 |
4 |
93 |
|
|
A csapatok között a 38-41. helyen végeztünk.
Bővebben itt.
|
| Előzmény: [97] Róbert Gida, 2012-07-14 19:19:15 |
|
|
| [96] Erben Péter | 2012-07-12 09:02:21 |
 Az 53. Nemzetközi Matematikai Diákolimpia feladatai
(Forrás: http://www.imo-official.org/problems.aspx )
1. feladat: Az ABC háromszög A csúccsal szemközti hozzáírt körének középpontja J. Ez a hozzáírt kör a BC oldalt az M pontban, az AB, ill. AC egyeneseket pedig a K, ill. L pontban érinti. Az LM és BJ egyenesek metszéspontja F, a KM és CJ egyenesek metszéspontja pedig G. Legyen S az AF és BC egyenesek metszéspontja, T pedig a AG és BC egyenesek metszéspontja.
Bizonyítsuk be, hogy M az ST szakasz felezőpontja.
2. feladat: Legyen n 3 egész, és legyenek a2,a3,...,an olyan pozitív valós számok, amelyekre a2.a3.....an=1. 3 egész, és legyenek a2,a3,...,an olyan pozitív valós számok, amelyekre a2.a3.....an=1.
Bizonyítsuk be, hogy
(1+a2)2(1+a3)3...(1+an)n>nn.
3. feladat: A hazudós játékot két játékos játssza: A és B. A játék szabályaiban szerepel két pozitív egész szám: k és n, ezek értékét mindkét játékos ismeri. A játék megkezdésekor A választ két egész számot: x-et és N-et, amikre 1 x x N. A az x számot titokban tartja, viszont N-et őszintén megmondja B-nek. B ezután megpróbál x-re vonatkozó információt szerezni A-tól a következő típusú kérdésekkel: B minden kérdésében megadja pozitív egész számok egy tetszőleges S halmazát (olyan S halmazt is megadhat, amit már korábban is megadott), és azt kérdezi A-tól, hogy x eleme-e ennek az S halmaznak. B akárhány ilyen típusú kérdést feltehet. A-nak B minden kérdésére a kérdés elhangzása után azonnal igennel vagy nemmel kell válaszolnia, de mindegyik válasza lehet hazugság is; az egyetlen kikötés az, hogy bármely egymás utáni k+1 válasz közül legalább egynek őszintének kell lennie. Miután B annyiszor kérdezett, ahányszor csak akart, meg kell neveznie egy legfeljebb n pozitív egész számból álló X halmazt. Ha x eleme az X halmaznak, akkor B nyer; különben B veszít. N. A az x számot titokban tartja, viszont N-et őszintén megmondja B-nek. B ezután megpróbál x-re vonatkozó információt szerezni A-tól a következő típusú kérdésekkel: B minden kérdésében megadja pozitív egész számok egy tetszőleges S halmazát (olyan S halmazt is megadhat, amit már korábban is megadott), és azt kérdezi A-tól, hogy x eleme-e ennek az S halmaznak. B akárhány ilyen típusú kérdést feltehet. A-nak B minden kérdésére a kérdés elhangzása után azonnal igennel vagy nemmel kell válaszolnia, de mindegyik válasza lehet hazugság is; az egyetlen kikötés az, hogy bármely egymás utáni k+1 válasz közül legalább egynek őszintének kell lennie. Miután B annyiszor kérdezett, ahányszor csak akart, meg kell neveznie egy legfeljebb n pozitív egész számból álló X halmazt. Ha x eleme az X halmaznak, akkor B nyer; különben B veszít.
Bizonyítsuk be:
1. Ha n 2k, akkor B-nek van nyerő stratégiája. 2k, akkor B-nek van nyerő stratégiája.
2. Minden elég nagy k-hoz van olyan n 1,99k egész szám, amire B-nek nincs nyerő stratégiája. 1,99k egész szám, amire B-nek nincs nyerő stratégiája.
4. feladat: Határozzuk meg az összes olyan f : Z Z függvényt, amire tetszőleges a,b,c egészekre, amelyekre a+b+c=0 teljesül, fennáll az Z függvényt, amire tetszőleges a,b,c egészekre, amelyekre a+b+c=0 teljesül, fennáll az
f(a)2+f(b)2+f(c)2=2f(a)f(b)+2f(b)f(c)+2f(c)f(a)
egyenlőség.
5. feladat: Legyen az ABC háromszögben BCA =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja. =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja.
Bizonyítsuk be, hogy MK=ML.
6. feladat: Határozzuk meg az összes olyan n pozitív egész számot, amelyhez találhatók olyan a1,a2,...,an nemnegatív egészek, amelyekre teljesül
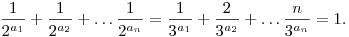
|
|
|
|
| [93] Gzoli | 2011-10-01 00:03:21 |
 Szia Lorantfy!
Nagyon köszönöm a gyors válaszodat, reakciódat. Sajnos jelenleg a honlap nem szuperál úgy ahogy kellene... reméljük holnapra várható valamiféle javulás. Mert már nagyon izgat egy-két feladat megoldása, így nem szeretnék várni kb. 2 hetet.
Üdvözlettel:
Gzoli
|
| Előzmény: [92] lorantfy, 2011-09-30 23:08:35 |
|
|
| [91] Gzoli | 2011-09-30 22:46:03 |
 Hello!
Engem nagyon érdekelnének az 52. Matematikai Diákolimpiai feladatok megoldásai. Valaki fel tudná ide tenni a megoldásokat? (vagy esetleg egy linket mellékelne ahol megtekinthetőek). Előre is köszönöm a fáradozást.
Üdvözlettel: Gzoli
|
|
|
|
| [88] Maga Péter | 2011-07-20 21:27:01 |
 A bónusz kérdésre válaszolok. Aki gondolkodni akar még rajta, ne olvasson tovább...
Szóval pozitív x-re legyen f(x)=-ex. Ez jó: 1. ha x 0, akkor a bal oldal nempozitív, a jobb oldal 0. 2. ha y 0, akkor a bal oldal nempozitív, a jobb oldal 0. 2. ha y 0, akkor a bal oldal nempozitív, a jobb oldalon f(f(x))=0, yf(x) nemnegatív, így a jobb oldal nemnegatív. 3. ha x,y>0, akkor az kell, hogy -ex+y 0, akkor a bal oldal nempozitív, a jobb oldalon f(f(x))=0, yf(x) nemnegatív, így a jobb oldal nemnegatív. 3. ha x,y>0, akkor az kell, hogy -ex+y -yex, ami fennáll, hiszen ey -yex, ami fennáll, hiszen ey y. y.
|
| Előzmény: [87] Erben Péter, 2011-07-20 10:16:53 |
|
|
| [86] Maga Péter | 2011-07-20 08:10:32 |
 ,,A végső indirekt részben az 1. esetben nem látom, miért létezik megfelelő y. Itt arról van szó, hogy A-nak nem lehet legnagyobb eleme?''
Nem, nem arról van szó: nem feltétlenül van A-nak legnagyobb eleme (legalábbis a priori). Talán egy kicsit pontatlanul fogalmaztam azzal, hogy 'legyen x, legyen y>0 ...'. Nem arról van szó, hogy választunk egy x-et A-ból, aztán egy pozitív y-t, hogy x+y is A-beli legyen, egyszerűen csak fogunk két A-beli elemet, a kisebbik x, a nagyobbik x+y, és ezekre írjuk fel a feltételt. Hogy van kettő, ehhez használjuk azt, hogy A kezdőszelet: így ha nemüres, végtelen sok eleme van.
|
| Előzmény: [84] Erben Péter, 2011-07-19 21:28:04 |
|
