Fórum: Matematikai Diákolimpia

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

Szeretnél hozzászólni? Jelentkezz be.

2013-07-25 15:22:47

Egyetértek. A 4. feladat végül is csak a gyakorolt versenyzőket szűri ki az összesből. Ismert trükkök vannak benne, demonstrálásképpen:

Legyen $\omega$ ₁ és $\omega$ ₂ másik metszéspontja P. Miquel tétele szerint ANMP húrnégyszög, viszont mivel M és N rajta van AH Thálesz-körén, így valójában APH $\angle$ =90°. Másrészt BCMN húrnégyszög, és a szelőtétel szerint AN^.AB=AM^.AC, amiből A rajta van $\omega$ ₁ és $\omega$ ₂ hatványvonalán, WP egyenesen. A Thálesz-tétel szerint P $\in$ XY, így APH $\angle$ =90° egyenértékűvé válik a feladat állításával, amit ezzel beláttunk.

Ugyancsak piskóta az 1.

A mostani 6. feladat azért még rendes az IMO2012 3. és 6. feladatához képest. Néhány működő, és kitaláható megoldás: .

Mindenesetre kíváncsi volnék a versenyzőink eredményeire.

Előzmény: [278] Ménkűnagy Bundáskutya, 2013-07-25 12:55:35

[278] Ménkűnagy Bundáskutya

2013-07-25 12:55:35

Ahogy én látom: az 1. és a 4. nagyon könnyűek; a 2. könnyű-közepes, legfeljebb közepes; a 3. és az 5. nehezek; a 6. őrült.

Minden gusztus dolga is. Aki síkgeometriában nem ügyes, annak a 3. már nagyon nehéz és a 4.-kel is megkínlódhat.

Előzmény: [277] w, 2013-07-25 07:25:19

[277] w

2013-07-25 07:25:19

Értékelésem szerint az 1. feladat nagyon könnyű, mindenknek meglett (csak két ötlet kell: indukció és vakon választott alkalmas számok). A 2. feladatot is legalább 4-en megoldják. A 3. feladat kicsit riasztó (mert 3. feladat), de könnyebb, mint a 2. feladat és így nagy eséllyel lesz 4-5 magyar megoldás. (Az 1. nap nekem kb. OKTV-nehézségűnek tűnik...)

2. napon viszont szerintem átlagosan 1,67 megoldott feladat várható.

Előzmény: [275] Ménkűnagy Bundáskutya, 2013-07-24 20:49:08

[276] w

2013-07-24 22:59:07

2013-as olimpia - 2. nap feladatai

4. feladat. Legyen ABC hegyesszögű háromszög magasságpontja H, és legyen W a BC oldal belső pontja. Jelölje M és N rendre a B-ből és C-ből húzott magasság talppontját. Jelölje $\omega$ ₁ a BWN kört, $\omega$ ₂ pedig a CWM kört. Végül pedig X és Y pont olyan, hogy XW, illetve YW az $\omega$ ₁, illetve $\omega$ ₂ kör átmérője. Mutassuk meg, hogy X, Y és H egy egyenesre esik.

5. feladat. Jelölje Q_>0 a pozitív racionális számok halmazát. Az f:Q_>0 $\to$ R függvény a következő feltételeket teljesíti:

(i) f(x)f(y) $\ge$ f(xy) ( $\forall$ x,y $\in$ Q_>0),

(ii) f(x+y) $\ge$ f(x)+f(y) ( $\forall$ x,y $\in$ Q_>0),

(iii) Létezik a>1 racionális szám, melyre f(a)=a.

Igazoljuk, hogy f(x)=x minden x $\in$ Q_>0 esetén.

6. feladat. Legyen n $\ge$ 3 egész szám, és tekintsük egy szabályos (n+1)-szög csúcsait és azoknak körülírt körét. Majd minden csúcsot megjelöljük a 0,1,...,n számok valamelyikével úgy, hogy minden szám pont egyszer szerepel. Két ilyen jelölést pontosan tekintünk különbözőnek, ha nem vihetők forgatással egymásba. Egy ilyen jelölést szépnek nevezünk, ha bármely a<b<c<d és a+d=b+c esetén az a és d-vel jelölt csúcsok közötti húr nem metszi a b és c jelű csúcsok közötti szakaszt.

Legyen M a szép jelölésrendszerek száma és N azon (x,y) pozitív egész számpárok száma, melyekre x+y $\le$ n és lnko(x,y)=1. Bizonyítsuk be, hogy M=N+1.

[275] Ménkűnagy Bundáskutya	2013-07-24 20:49:08
Nagyon kellemes, csinos kis feladat a 2-es. Kombinatorikus geometria, ezért joggal remélhetjük, hogy jól szereplünk rajta. Talán 2. példának kicsit könnyű, de ez legyen a legnagyobb bajunk.
Előzmény: [272] w, 2013-07-24 13:08:08

[274] w	2013-07-24 17:03:45
Igen, köszönöm. Javítás: Melyik a legkisebb egyenesszám, amely minden esetben elegendő?
Előzmény: [273] Maga Péter, 2013-07-24 16:24:06

[273] Maga Péter

2013-07-24 16:24:06

,,Legalább hány egyenesre lesz szükségünk biztosan?''

Értendő: legalább hány egyenes elegendő biztosan?:)

Előzmény: [272] w, 2013-07-24 13:08:08

[272] w

2013-07-24 13:08:08

2013-as olimpia - 1. nap feladatai

1. feladat. Legyen k és n tetszőleges pozitív egész szám. Mutassuk meg, hogy létezik m₁, m₂, ..., m_k pozitív egészekből álló számsorozat úgy, hogy

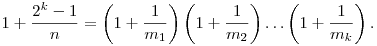
$1+\frac{2^k-1}n=\left(1+\frac1{m_1}\right)\left(1+\frac1{m_2}\right)\dots\left(1+\frac1{m_k}\right).$

2. feladat. Adott a síkon 2013 számú piros pont és 2014 darab kék pont úgy, hogy nincs közülük három egy egyenesen. A síkot az előbbiek közül egyik pontra sem illeszkedő egyenesekkel olyan tartományokra szeretnénk bontani, melyek nem tartalmaznak egyszerre piros és kék pontot. Legalább hány egyenesre lesz szükségünk biztosan?

3. feladat. ABC háromszög megfelelő hozzáírt körei rendre A₁, B₁, C₁ pontokban érintik a BC, CA, AB oldalszakaszokat. Bizonyítsuk be, hogy ha A₁B₁C₁ háromszög körülírt körének középpontja illeszkedik ABC háromszög körülírt körére, akkor ABC háromszög derékszögű!

(Itt találhatók megoldások, megoldási ötletek.)

[271] Kós Géza

2013-04-01 08:37:29

Szintén április 1. alkalmából:

Sikeresek vagyunk, kezünkben az agyunk

(Emlékezetes videoklip a 2007-es, matematikai diákolimpiáról, vietnamból)

[270] w

2013-03-26 21:44:01

Nem vagyok technofil, nem voltam válogatóversenyen, és csupán érdekelt a feladatok megoldása, hátha magas szintű eszközök/nehéz ötletek kellenek hozzájuk. Korábban is raktak fel feladatsort, csak a dátumot nem figyeltem. Nem akartam rosszat. Ha nagyon-nagyon akarnám, párszáz telefonhívással meghatározhatnám a shortlist feladatait, csak valami okból ezt nem teszem meg.

Előzmény: [268] Fálesz Mihály, 2013-03-24 22:07:19

[269] Róbert Gida	2013-03-26 16:10:51
Anno még úgy ment az olimpiai válogató, hogy régi olimpiai feladatok voltak. Az egész nem volt több, mint egy memória verseny.
Előzmény: [268] Fálesz Mihály, 2013-03-24 22:07:19

[268] Fálesz Mihály

2013-03-24 22:07:19

Részlet az angol csapatvezető egy korábbi olimpiai beszámolójából.

Traditionally the shortlist of candidate questions for the previous IMO is kept secret for one year so that the contents can be used for selection purposes. This sensible system has been undermined by the internet, human folly and the ever increasing size of the IMO. It is bad enough relying on 90 other leaders to be discreet. Now as soon as a selection test is sat somewhere in the world, some candidates are driven by a technophilic compulsion to put the paper on the internet within three minutes of leaving the exam hall. Unless candidates are confined to lead-lined wi-fi-proof chambers (an attractive idea) there seems no way to stop this incontinence. Once a question appears on a couple of selection tests, then it doesn’t take the students long to work out that it was on the IMO shortlist last year, and to prepare a model answer in case their leader is sufficiently unworldly as to trust the security of the shortlist.

Előzmény: [267] w, 2013-03-24 19:41:42

[267] w	2013-03-24 19:41:42
Bocsánatot kérek, nem tudtam.
Előzmény: [266] Moderátor, 2013-03-24 19:20:46

[266] Moderátor

2013-03-24 19:20:46

w hozzászólását töröltem.

A válogatóversenyen olyan feladat is szerepelt, ami a legutóbbi olimpiai shortlistben szerepel, ezért az olimpia végéig titkos.

[264] Róbert Gida

2013-03-13 22:52:20

Jó kérdés, mondjuk egy Freud előadást feltettek idén: Freud

ps. A kivetítőt nem látod a felvételen. Ez azért elég sokat levon a felvétel értékéből.

Előzmény: [262] w, 2013-03-13 22:19:30

[263] w	2013-03-13 22:20:58
Mostanában volt a válogatóverseny, a feladatokat és esetleges megoldásokat írhatnánk ide.

[262] w	2013-03-13 22:19:30
Miért nem veszik fel mostanában az olimpiai szakköröket?

[261] Róbert Gida	2012-11-10 11:59:56
Ha a megoldás, akkor c*a is, így racionális megoldásból van kisebb, de nincs legkisebb, hiszen az origóhoz tetszőlegesen közeli megoldás van. Amit viszont lehet csinálni: egészértékűségi feltételt elhagyva nemlineáris programozási feladatként nézni és az optimális megoldást megkeresni. n=25-re így is találtak ellenpéldát.
Előzmény: [260] Lóczi Lajos, 2012-11-10 00:55:00

[260] Lóczi Lajos	2012-11-10 00:55:00
És vajon lehet még jobb ellenpéldák sorozatát adni, ha elhagyjuk az egészértékűségi feltételt? Le lehet valahogy írni az ellenpéldák halmazát?
Előzmény: [259] Róbert Gida, 2012-11-09 20:01:53

[259] Róbert Gida

2012-11-09 20:01:53

Dinamikus programozással jön ki, némi trükkel. Olyan n tagot szeretnénk találni, ahol minden tag legfeljebb M és a reciprokösszeg a Shapiroban kisebb, mint 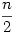$\frac n2$ . Legyen az első és második tag fix a₁=c₁,a₂=c₂ és $dp[k][x][y]=min({\sum_{i=1}^{k-2} \frac{a_i}{a_{i+1}+a_{i+2}}: a_1=c_1;a_2=c_2;a_{k-1}=x;a_k=y})$

Ez k=2-re dp[2][c₁][c₂]=0 egyébként végtelen (de gépen írhatunk például 1000-et végtelen helyett). Ha adott k-ra ismert az egész dp[k][][] tömb, akkor könnyen ki tudjuk számolni a dp[k+1][][] tömböt is, figyelve arra, hogy 2 egymásutáni tag nem lehet nulla. k-val (n-2)-is megyünk el, ott megállhatunk, hiszen az utolsó két tag és az első 2 tag ismert dp[n-2][][]-nél, így az utolsó 2 reciprok is. Ezért is kellett az első 2 tagot rögzíteni, hogy az egyenlőtlenségbeli ciklikusságot kilőjük.

Valójában nem kell 3 dimenziós tömb itt, hiszen mi csak a dp[k][][] értékeket használunk dp[k+1][][] kiszámításához. Ha megoldást találunk akkor viszont kell egy 3 ds tömb a tagok visszakereséséhez (vagy memória helyett a futási időt is növelhetjük).

Egy további bónusz, hogy adott n,M-re azt az (egyik) n tagú megoldást is megkaphattuk, amire a reciprokösszeg minimális a Shapiro egyenlőtlenségben. Amiket megadtam megoldások azok ezt is tudják.

Előzmény: [258] Lóczi Lajos, 2012-11-09 18:19:08

[258] Lóczi Lajos	2012-11-09 18:19:08
Azt hogyan tudod bizonyítani, hogy ezek az ellenpéldák a legjobbak, vagyis, hogy a maximális elem minimális?
Előzmény: [257] Róbert Gida, 2012-11-09 16:19:47

[257] Róbert Gida

2012-11-09 16:19:47

1 óra 42 percnél Pelikán megadott egy ismert ellenpéldát Shapiro egyenlőtlenségére n=14 (egész) taggal. Némi munkával található "jobb" ellenpélda is, ahol a maximális tag kisebb. Sőt megtalálható ilyen értelemben véve legjobb ellenpélda, ez pedig:

a=[1,31,0,33,0,35,2,35,4,33,4,31,3,30], erre: 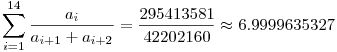$\sum_{i=1}^{14}\frac {a_i}{a_{i+1}+a_{i+2}}=\frac{295413581}{42202160}\approx 6.9999635327$

Nem adott viszont ellenpéldát a páratlan n=25-re. Íme a legjobb ellenpélda itt, ez a szörnyeteg: legyen a=[3,14,1,16,0,19,0,23,0,27,2,30,8,28,13,23,15,18,15,13,14,9,13,6,13], ekkor: 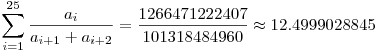$\sum_{i=1}^{25}\frac {a_i}{a_{i+1}+a_{i+2}}=\frac{1266471222407}{101318484960}\approx 12.4999028845$

[256] Róbert Gida

2012-11-08 18:41:54

2. szakkör:

http://www.youtube.com/watch?v=bqbBc2AxSyU&feature=g-all-u

[255] Hölder	2012-10-20 00:31:57
Valóban nem lehet látni, hogy mit írnak a táblára, de mindent mond,és ennyi elég is, még akkor is ha éppen ott vagy, mert egyáltalán nem gyorsan írja és mondja a dolgokat. Ettől függetlenül valóban érdemes lenne valamit csinálni a kamerával. Az ötletet, hogy felveszik az előadásokat,üdvözlöm,ha nem kerül túl sokba,érdemes lenne Dobos tanár úróráit is felvenni.
Előzmény: [251] pvong17, 2012-10-07 22:21:10

[254] vogel

2012-10-12 20:56:23

A youtube is konvertálja a videót, az is sokat ronthat. Szintén, a nem HD videót is érdemes HD-ként feltölteni emiatt. (Vagy erre is gondoltál többek közt.)

De a linkeden fél tábla méretű betűkkel írnak. :D

Előzmény: [253] pvong17, 2012-10-11 13:58:24

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15]

Már regisztráltál?
Új vendég vagy?