| [294] Kós Géza | 2014-07-11 22:09:39 |
 A 2014-es eredmények:
|
1 |
2 |
3 |
4 |
5 |
6 |
összesen |
helyezés |
díj |
| Fehér Zsombor |
7 |
7 |
6 |
7 |
7 |
1 |
35 |
15-24 |
aranyérem |
| Di Giovanni Márk |
7 |
7 |
0 |
7 |
6 |
0 |
27 |
69-82 |
ezüstérem |
| Ágoston Péter |
7 |
7 |
0 |
7 |
0 |
5 |
26 |
83-94 |
ezüstérem |
| Homonnay Bálint |
7 |
7 |
0 |
7 |
2 |
0 |
23 |
109-123 |
ezüstérem |
| Janzer Barnabás |
7 |
7 |
0 |
7 |
1 |
0 |
22 |
124-162 |
ezüstérem |
| Maga Balázs |
7 |
7 |
0 |
4 |
2 |
0 |
20 |
200-220 |
bronzérem |
| csapat: |
42 |
42 |
6 |
39 |
18 |
6 |
153 |
15 |
|
|
|
| Előzmény: [293] Maga Balázs, 2014-07-11 19:44:43 |
|
| [293] Maga Balázs | 2014-07-11 19:44:43 |
 Valószínűsíthető pontszámok:
Ágoston Péter: 7+7+0+7+0+5
Di Giovanni Márk: 7+7+0+7?+6+0
Fehér Zsombor: 7+7+6+7+7+1
Homonnay Bálint: 7+7+0+7+2+0
Janzer Barnabás: 7+7+0+7+1+0
Maga Balázs 7+7+0+4+2+0
|
|
| [292] w | 2014-07-10 19:46:19 |
 Egyébként az ez évi válogatóversenyek feladatai: ISL 2013 N1, G4, A4; illetve A2, N3, G5.
|
|
| [291] w | 2014-07-10 18:00:34 |
 Igazán nincs mit. Egyébként a 4. feladatban kikötötték még, hogy &tex;\displaystyle ABC&xet; háromszög hegyesszögű.
Ha valaki kíváncsi rá, a kitűző országok rendre Ausztria, Horvátország, Irán, Grúzia, Luxemburg és Ausztria (ill. USA).
Mit szóltok a feladatsor minőségéről, nehézségéről? Nekem úgy tűnt, hogy ez a tipikus IMO-hoz kevésbé hasonlított, mint a Kürschák-versenyre. Ilyen jellegű, kombinatorikus feladatsorok felé kellene mozdulni, vagy az utóbbi két évben látott "kiegyensúlyozottabb" feladatsorok jobbak voltak?
|
| Előzmény: [290] jonas, 2014-07-10 09:07:17 |
|
|
| [289] w | 2014-07-09 19:12:28 |
 2014-es olimpia - 2. nap feladatai.
4. feladat. Legyen &tex;\displaystyle P&xet; és &tex;\displaystyle Q&xet; az &tex;\displaystyle ABC&xet; háromszög &tex;\displaystyle BC&xet; oldalának belső pontja úgy, hogy &tex;\displaystyle PAB\angle=BCA\angle&xet; és &tex;\displaystyle CAQ\angle=ABC\angle&xet;. Az &tex;\displaystyle M&xet; és &tex;\displaystyle N&xet; pontok olyanok, hogy &tex;\displaystyle P&xet; az &tex;\displaystyle AM&xet; szakasz, &tex;\displaystyle Q&xet; az &tex;\displaystyle AN&xet; szakasz felezőpontja. Mutassuk meg, hogy &tex;\displaystyle BM&xet; és &tex;\displaystyle CN&xet; egyenesek &tex;\displaystyle ABC&xet; háromszög körülírt körén metszik egymást.
5. feladat. Fokváros bankja &tex;\displaystyle \frac1n&xet; értékű pénzérméket forgalmaz, bármely pozitív &tex;\displaystyle n&xet;-nel. Van nálunk néhány fokvárosi pénzérme, melyek értéke összesen nem haladja meg a &tex;\displaystyle 99+\frac12&xet;-et. Mutassuk meg, hogy ezek a pénzérmék szétoszthatók &tex;\displaystyle 100&xet; darab csoportba úgy, hogy minden csoportban az érmék összértéke nem haladja meg az &tex;\displaystyle 1&xet;-et.
6. feladat. Egy síkbeli véges egyeneshalmazt általános helyzetűnek mondunk, ha nincs köztük kettő párhuzamos, és semelyik három sem halad át egy ponton. Néhány síkbeli egyenes a síkot az egyenesek által tovább nem darabolható részekre osztja, ezek közül a korlátos részeket nevezzük véges síkrésznek. Mutassuk meg, hogy elég nagy &tex;\displaystyle n&xet; esetén &tex;\displaystyle n&xet; darab általános helyzetű egyenes közül lehetséges minimum &tex;\displaystyle \sqrt n&xet; darabot kékre színezni oly módon, hogy a véges síkrészek közül egyiket se csak kék egyenesek határolják.
Megjegyzés. Ha &tex;\displaystyle \sqrt n&xet; helyett &tex;\displaystyle c\sqrt n&xet; értékre bizonyítjuk be az állítást, &tex;\displaystyle c<1&xet; nagyságától függő részpontszámok kaphatók.
|
|
| [288] w | 2014-07-08 17:45:21 |
 2014-es olimpia - 1. nap feladatai.
1. feladat. Tekintsünk egy pozitív egészekből álló &tex;\displaystyle a_0<a_1<a_2<\dots&xet; végtelen sorozatot. Mutassuk meg, hogy egyértelműen létezik olyan &tex;\displaystyle n\ge 1&xet; egész szám, melyre
&tex;\displaystyle a_n<\frac{a_0+a_1+\dots+a_n}n\le a_{n+1}.&xet;
2. feladat. Legyen &tex;\displaystyle n\ge 2&xet; egész szám, és tekintsünk egy &tex;\displaystyle n\times n&xet;-es (&tex;\displaystyle n^2&xet; darab mezőből álló) sakktáblát. A sakktáblán bástyákat helyezünk el. Nevezzük békésnek &tex;\displaystyle n&xet; darab bástya olyan elrendezését, melyben nincs két bástya egy sorban vagy oszlopban. Határozzuk meg azt a legnagyobb pozitív egész &tex;\displaystyle k&xet; számot, amelyre teljesül, hogy bármely békés elrendezésben van egy &tex;\displaystyle k\times k&xet; méretű négyzet, melynek &tex;\displaystyle k^2&xet; mezője közül egyiken sincs bástya.
3. feladat. Az &tex;\displaystyle ABCD&xet; konvex négyszögben &tex;\displaystyle ABC\angle =CDA\angle =90^\circ&xet;. Az &tex;\displaystyle A&xet;-ból &tex;\displaystyle BD&xet;-re állított merőleges talppontja &tex;\displaystyle H&xet;. Adottak az &tex;\displaystyle S&xet; és &tex;\displaystyle T&xet; pontok az &tex;\displaystyle AB&xet;, illetve &tex;\displaystyle AD&xet; szakaszon úgy, hogy &tex;\displaystyle H&xet; az &tex;\displaystyle SCT&xet; háromszög belső pontja, továbbá
&tex;\displaystyle CHS\angle - CSB\angle = THC\angle -DTC\angle =90^\circ.&xet;
Mutassuk meg, hogy &tex;\displaystyle BD&xet; egyenes érinti a &tex;\displaystyle TSH&xet; háromszög köré írható kört.
|
|
| [287] Maga Péter | 2013-07-27 12:17:48 |
 Gratulálok az egész csapatnak!
A tavalyi gyengébb szereplés után jó látni, hogy az 1. és a 4. feladatot mindenki 7 ponttal hozta, és még a 2. feladaton is sok pontot sikerült szerezni.
Ami a nehéz feladatokat illeti, ott is jobban szerepeltünk a tavalyinál. A bika 6. mindenkin kifogott, de Olivér és Attila is levadásztak egy-egy nehéz példát.
|
| Előzmény: [285] Kós Géza, 2013-07-27 04:56:33 |
|
|
| [285] Kós Géza | 2013-07-27 04:56:33 |
 A eredmények:
|
1 |
2 |
3 |
4 |
5 |
6 |
összesen |
díj |
| Fehér Zsombor |
7 |
2 |
0 |
7 |
0 |
0 |
16 |
bronzérem |
| Havasi Márton |
7 |
7 |
0 |
7 |
0 |
0 |
21 |
bronzérem |
| Janzer Olivér |
7 |
7 |
0 |
7 |
7 |
0 |
28 |
ezüstérem |
| Nagy Róbert |
7 |
7 |
2 |
7 |
0 |
0 |
23 |
bronzérem |
| Szabó Attila |
7 |
2 |
7 |
7 |
1 |
0 |
24 |
ezüstérem |
| Tardos Jakab |
7 |
7 |
0 |
7 |
1 |
0 |
22 |
bronzérem |
| Összesen: |
42 |
32 |
9 |
42 |
9 |
0 |
134 |
|
|
Csapatban 22-24. hely.
|
|
| [284] w | 2013-07-26 23:11:51 |
 "Muszáj ezt?" - ha semmilyen megoldási ötletet sem akartál volna látni, csak a feladatokat olvastad volna el. Amúgy is, a két leírt trükk ismert, és más úton nem is lehetne elindulni.
"nem lesz." - igazad van, sajnos közelről sem lesz :-(
|
| Előzmény: [283] Sinobi, 2013-07-26 22:48:08 |
|
| [283] Sinobi | 2013-07-26 22:48:08 |
 ,,(csak két ötlet kell: indukció és vakon választott alkalmas számok). "
muszáj ezt? (mondjuk most már mindegy)
,,A 3. feladat kicsit riasztó (mert 3. feladat), de könnyebb, mint a 2. feladat és így nagy eséllyel lesz 4-5 magyar megoldás. "
nem lesz.
|
| Előzmény: [277] w, 2013-07-25 07:25:19 |
|
|
|
|
| [279] w | 2013-07-25 15:22:47 |
 Egyetértek. A 4. feladat végül is csak a gyakorolt versenyzőket szűri ki az összesből. Ismert trükkök vannak benne, demonstrálásképpen:
Legyen  1 és 1 és  2 másik metszéspontja P. Miquel tétele szerint ANMP húrnégyszög, viszont mivel M és N rajta van AH Thálesz-körén, így valójában APH 2 másik metszéspontja P. Miquel tétele szerint ANMP húrnégyszög, viszont mivel M és N rajta van AH Thálesz-körén, így valójában APH =90°. Másrészt BCMN húrnégyszög, és a szelőtétel szerint AN.AB=AM.AC, amiből A rajta van =90°. Másrészt BCMN húrnégyszög, és a szelőtétel szerint AN.AB=AM.AC, amiből A rajta van  1 és 1 és  2 hatványvonalán, WP egyenesen. A Thálesz-tétel szerint P 2 hatványvonalán, WP egyenesen. A Thálesz-tétel szerint P XY, így APH XY, így APH =90° egyenértékűvé válik a feladat állításával, amit ezzel beláttunk. =90° egyenértékűvé válik a feladat állításával, amit ezzel beláttunk.
Ugyancsak piskóta az 1.
A mostani 6. feladat azért még rendes az IMO2012 3. és 6. feladatához képest. Néhány működő, és kitaláható megoldás: .
Mindenesetre kíváncsi volnék a versenyzőink eredményeire.
|
| Előzmény: [278] Ménkűnagy Bundáskutya, 2013-07-25 12:55:35 |
|
| [278] Ménkűnagy Bundáskutya | 2013-07-25 12:55:35 |
 Ahogy én látom: az 1. és a 4. nagyon könnyűek; a 2. könnyű-közepes, legfeljebb közepes; a 3. és az 5. nehezek; a 6. őrült.
Minden gusztus dolga is. Aki síkgeometriában nem ügyes, annak a 3. már nagyon nehéz és a 4.-kel is megkínlódhat.
|
| Előzmény: [277] w, 2013-07-25 07:25:19 |
|
| [277] w | 2013-07-25 07:25:19 |
 Értékelésem szerint az 1. feladat nagyon könnyű, mindenknek meglett (csak két ötlet kell: indukció és vakon választott alkalmas számok). A 2. feladatot is legalább 4-en megoldják. A 3. feladat kicsit riasztó (mert 3. feladat), de könnyebb, mint a 2. feladat és így nagy eséllyel lesz 4-5 magyar megoldás. (Az 1. nap nekem kb. OKTV-nehézségűnek tűnik...)
2. napon viszont szerintem átlagosan 1,67 megoldott feladat várható.
|
| Előzmény: [275] Ménkűnagy Bundáskutya, 2013-07-24 20:49:08 |
|
| [276] w | 2013-07-24 22:59:07 |
 2013-as olimpia - 2. nap feladatai
4. feladat. Legyen ABC hegyesszögű háromszög magasságpontja H, és legyen W a BC oldal belső pontja. Jelölje M és N rendre a B-ből és C-ből húzott magasság talppontját. Jelölje  1 a BWN kört, 1 a BWN kört,  2 pedig a CWM kört. Végül pedig X és Y pont olyan, hogy XW, illetve YW az 2 pedig a CWM kört. Végül pedig X és Y pont olyan, hogy XW, illetve YW az  1, illetve 1, illetve  2 kör átmérője. Mutassuk meg, hogy X, Y és H egy egyenesre esik. 2 kör átmérője. Mutassuk meg, hogy X, Y és H egy egyenesre esik.
5. feladat. Jelölje Q>0 a pozitív racionális számok halmazát. Az f:Q>0 R függvény a következő feltételeket teljesíti: R függvény a következő feltételeket teljesíti:
(i) f(x)f(y) f(xy) ( f(xy) ( x,y x,y Q>0), Q>0),
(ii) f(x+y) f(x)+f(y) ( f(x)+f(y) ( x,y x,y Q>0), Q>0),
(iii) Létezik a>1 racionális szám, melyre f(a)=a.
Igazoljuk, hogy f(x)=x minden x Q>0 esetén. Q>0 esetén.
6. feladat. Legyen n 3 egész szám, és tekintsük egy szabályos (n+1)-szög csúcsait és azoknak körülírt körét. Majd minden csúcsot megjelöljük a 0,1,...,n számok valamelyikével úgy, hogy minden szám pont egyszer szerepel. Két ilyen jelölést pontosan tekintünk különbözőnek, ha nem vihetők forgatással egymásba. Egy ilyen jelölést szépnek nevezünk, ha bármely a<b<c<d és a+d=b+c esetén az a és d-vel jelölt csúcsok közötti húr nem metszi a b és c jelű csúcsok közötti szakaszt. 3 egész szám, és tekintsük egy szabályos (n+1)-szög csúcsait és azoknak körülírt körét. Majd minden csúcsot megjelöljük a 0,1,...,n számok valamelyikével úgy, hogy minden szám pont egyszer szerepel. Két ilyen jelölést pontosan tekintünk különbözőnek, ha nem vihetők forgatással egymásba. Egy ilyen jelölést szépnek nevezünk, ha bármely a<b<c<d és a+d=b+c esetén az a és d-vel jelölt csúcsok közötti húr nem metszi a b és c jelű csúcsok közötti szakaszt.
Legyen M a szép jelölésrendszerek száma és N azon (x,y) pozitív egész számpárok száma, melyekre x+y n és lnko(x,y)=1. Bizonyítsuk be, hogy M=N+1. n és lnko(x,y)=1. Bizonyítsuk be, hogy M=N+1.
|
|
| [275] Ménkűnagy Bundáskutya | 2013-07-24 20:49:08 |
 Nagyon kellemes, csinos kis feladat a 2-es. Kombinatorikus geometria, ezért joggal remélhetjük, hogy jól szereplünk rajta. Talán 2. példának kicsit könnyű, de ez legyen a legnagyobb bajunk.
|
| Előzmény: [272] w, 2013-07-24 13:08:08 |
|
|
|
| [272] w | 2013-07-24 13:08:08 |
 2013-as olimpia - 1. nap feladatai
1. feladat. Legyen k és n tetszőleges pozitív egész szám. Mutassuk meg, hogy létezik m1, m2, ..., mk pozitív egészekből álló számsorozat úgy, hogy
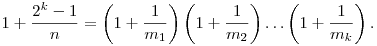
2. feladat. Adott a síkon 2013 számú piros pont és 2014 darab kék pont úgy, hogy nincs közülük három egy egyenesen. A síkot az előbbiek közül egyik pontra sem illeszkedő egyenesekkel olyan tartományokra szeretnénk bontani, melyek nem tartalmaznak egyszerre piros és kék pontot. Legalább hány egyenesre lesz szükségünk biztosan?
3. feladat. ABC háromszög megfelelő hozzáírt körei rendre A1, B1, C1 pontokban érintik a BC, CA, AB oldalszakaszokat. Bizonyítsuk be, hogy ha A1B1C1 háromszög körülírt körének középpontja illeszkedik ABC háromszög körülírt körére, akkor ABC háromszög derékszögű!
(Itt találhatók megoldások, megoldási ötletek.)
|
|
| [271] Kós Géza | 2013-04-01 08:37:29 |
 Szintén április 1. alkalmából:
Sikeresek vagyunk, kezünkben az agyunk

(Emlékezetes videoklip a 2007-es, matematikai diákolimpiáról, vietnamból)
|
|
| [270] w | 2013-03-26 21:44:01 |
 Nem vagyok technofil, nem voltam válogatóversenyen, és csupán érdekelt a feladatok megoldása, hátha magas szintű eszközök/nehéz ötletek kellenek hozzájuk. Korábban is raktak fel feladatsort, csak a dátumot nem figyeltem. Nem akartam rosszat. Ha nagyon-nagyon akarnám, párszáz telefonhívással meghatározhatnám a shortlist feladatait, csak valami okból ezt nem teszem meg.
Amúgy egy másik részlet az olimpiai beszámolóból: ©2006 G. C. Smith. ;-)
|
| Előzmény: [268] Fálesz Mihály, 2013-03-24 22:07:19 |
|
