|
| [66] Kós Géza | 2010-07-08 10:52:53 |
 Íme az idei feladatok.
Első nap
1. feladat. Határozzuk meg az összes olyan f:R R függvényt, amelyre az R függvényt, amelyre az
f([x]y)=f(x)[f(y)]
egyenlőség teljesül minden x,y R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.) R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.)
Javasolta: Franciaország
2. feladat. Legyen I az ABC háromszög beírt körének középpontja,  pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a  körrel legyen D. Legyen E a BDC körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül körrel legyen D. Legyen E a BDC körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül
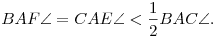
Legyen továbbá G az IF szakasz középpontja. Bizonyítsuk be, hogy a DG és EI egyenesek a  körön metszik egymást. körön metszik egymást.
Javasolta: Hong Kong
3. feladat. Legyen N a pozitív egész számok halmaza. Határozzuk meg az összes olyan g:N N függvényt, amelyre N függvényt, amelyre
(g(m)+n)(m+g(n))
teljes négyzet minden m,n N-re. N-re.
Javasolta: USA
Második nap
4. feladat. Legyen P egy pont az ABC háromszög belsejében. Az AP, BP és CP egyenesek másik metszéspontja az ABC háromszög  körülírt körével legyen rendre K, L és M. A körülírt körével legyen rendre K, L és M. A  körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML. körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML.
Javasolta: Lengyelország
5. feladat. A B1,B2,B3,B4,B5,B6 dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:
1. típusú lépés: Választunk egy Bj nemüres dobozt, ahol 1 j j 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz. 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz.
2. típusú lépés: Választunk egy Bk nemüres dobozt, ahol 1 k k 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával. 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával.
Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B1, B2, B3, B4, B5 dobozok mindegyike üres legyen, a B6 doboz pedig pontosan 201020102010 érmét tartalmazzon. (Definíció szerint abc=a(bc).)
Javasolta: Hollandia
6. feladat. Legyen a1,a2,a3,... pozitív valós számok egy sorozata. Tegyük fel, hogy van egy olyan s pozitív egész, amellyel
an=max {ak+an-k | 1 k k n-1} n-1}
teljesül minden n>s egészre. Bizonyítsuk be, hogy léteznek olyan  és N pozitív egészek, amikre és N pozitív egészek, amikre   s, és s, és 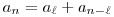 minden n minden n N-re. N-re.
Javasolta: Irán
|
|
|
|
| [63] lorantfy | 2009-07-24 16:14:38 |
 Gratulálok a csapat minden tagjának és a felkészítő tanároknak!
|
|
| [62] Python | 2009-07-23 12:32:55 |
 Gratulálok a csapatnak!
|
|
| [61] Láda19 | 2009-07-23 07:03:43 |
 Biztosak vagyunk abban, hogy mindent megtettetek az eredményes szereplés érdekében. Mnd a hatan érmet szereztetek, ez szép teljesítmény. Gratulálok a csapatnak, és mindannyiótoknak további sikeres és eredményes munkát kívánok.
|
| Előzmény: [60] janomo, 2009-07-22 20:19:23 |
|
|
|
|
|
| [56] m2mm | 2009-07-19 14:25:26 |
 Mármint
Tomon István 7 7 7 7 7 0 35 Gold medal
Szűcs Gergely 7 7 1 0 3 0 18 Bronze medal
Nagy János 7 7 7 2 7 0 30 Silver medal
Nagy Dániel 7 7 1 5 3 0 23 Bronze medal
Kornis Kristóf 7 7 0 2 7 0 23 Bronze medal
Éles András 7 7 2 5 7 0 28 Silver medal
|
| Előzmény: [55] m2mm, 2009-07-19 14:23:03 |
|
| [55] m2mm | 2009-07-19 14:23:03 |
 Gratulálok a magyar csapat tagjainak!
Az eredmények:
Tomon István 7 7 7 7 7 0 35 Gold medal
Szűcs Gergely 7 7 1 0 3 0 18 Bronze medal
Nagy János 7 7 7 27 0 30 Silver medal
Nagy Dániel 7 7 1 53 0 23 Bronze medal
Kornis Kristóf 7 7 0 27 0 23 Bronze medal
Éles András 7 7 2 57 0 28 Silver medal
|
|
| [54] Kós Géza | 2009-07-17 18:09:41 |
 Az idei feladatok
(Szabad fordításban)
I. nap
1. feladat. Legyen n pozitív egész, és legyenek a1,a2,a3,...,ak (k 2) különbző egészek az {1,2,...,n} halmazból úgy, hogy ai(ai+1-1) osztható n-nel minden egyes i=1,2,...,k-1 esetén. Bizonyítsuk be, hogy ak(a1-1) nem osztható n-nel. 2) különbző egészek az {1,2,...,n} halmazból úgy, hogy ai(ai+1-1) osztható n-nel minden egyes i=1,2,...,k-1 esetén. Bizonyítsuk be, hogy ak(a1-1) nem osztható n-nel.
2. feladat. Az ABC háromszög köré írt kör középpontja O. P és Q belső pontjai a CA, illetve AB oldalaknak. Legyen K, L és M a BP, CQ, illetve PQ szakaszok felezőpontja, és legyen  a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha  érinti a PQ egyenest, akkor OP=OQ. érinti a PQ egyenest, akkor OP=OQ.
3. feladat. Tegyük fel, hogy s1,s2,s3,... egy pozitív egészekből álló, szigorúan növekvő sorozat, amire az ss1,ss2,ss3,... és ss1+1,ss2+1,ss3+1,... részsorozatok számtani sorozatok. Bizonyítsuk be, hogy s1,s2,s3,... maga is számtani sorozat.
II. nap
4. feladat. Az ABC háromszögben AB=AC. A CAB és az ABC szög felezője a BC és CA olalakat D-ben, illetve E-ben metszi. Legyen K az ADC háromszögbe írt kör középpontja. Tegyük fel, hogy BEK =45o. Határozzuk meg a CAB szög összes lehetséges értékét. =45o. Határozzuk meg a CAB szög összes lehetséges értékét.
5. feladat. Határozzuk meg az összes olyan, a pozitív egészek halmazából a pozitív egészek halmazába képező f függvényt, amire tetszőleges a,b pozitív egészek esetén az a, f(b) és f(b+f(a)-1) hosszúságú szakaszokból (nem elfajuló) háromszög szerkeszthető.
6. feladat. Legyenek a1,a2,...,an különböző pozitív egészek, és legyen M egy n-1 pozitív egészből álló halmaz, ami nem tartalmazza az s=a1+a2+...+an számot. Egy szöcskének, a számegyenes 0 pontjából indulva, összesen n-szer kell ugrania jobb felé úgy, hogy az ugrások hossza rendre a1,a2,...,an legyen valamilyen sorrendben. Bizonyítsuk be, hogy az ugrások sorrendjét meg tudjuk választani úgy, hogy a szöcske egyszer se lépjen M-beli pontra.
|
|
| [53] lorantfy | 2008-07-24 19:56:22 |
 GRATULÁLOK A MAGYAR CSAPAT MINDEN TAGJÁNAK!
|
 |
|
| [52] Diego2 | 2008-07-21 18:53:57 |
 Nagyon nagy dolog, amit a fiúk műveltek. Ez nem vicc, gyerekek. Le a kalappal! Gratulálok az egész magyar csapatnak és mindenkinek, akinek ehhez a világraszóló sikerhez valamilyen köze van! Mert tetszik van nem, igenis, többek között az ilyen tudás az IGAZI ÉRTÉK! Nem lehet pénzben kifejezni.
|
|
|
| [50] Róbert Gida | 2008-07-20 18:38:52 |
 Eredmények:
http://www.imo-2008.es/results.html
Lovász fia negyedik lett az összes induló között, másodikban vesztett pontot.
Ezt a számolós második példának az a részét beadtam a Mathematica-nak, nem tudta bebizonyítani, tehát annyira mégsem könnyű, legalábbis egy gépnek. Csak a teljesen triviális jobboldal=0-át tudta belátni.
|
|
|
|
| [47] sakkmath | 2008-07-18 16:54:09 |
 Ha jó angolul is, klikk ide. Itt az "S"-ikonokra kattintva a megoldásokhoz jutunk. Magyarul két lehetőség adódik:
1) Egy könyv: Reiman István - Dobos Sándor: Nemzetközi Matematikai Diákolimpiák 1959 - 2003 (TypoTex, 2000, ISBN : 9639548045);
2) Egy lap: KöMaL 2000. év októberi száma. (Legalábbis ebben kell lennie, ugyanis az elmúlt évek gyakorlata ez: a szeptemberi számban a feladatokat és a beszámolót közlik, s a következőben hozzák a magyar olimpikonok megoldásait.
|
| Előzmény: [46] m2mm, 2008-07-18 12:58:42 |
|
| [46] m2mm | 2008-07-18 12:58:42 |
 Üdv! Valaki megtudná mondani, hol találhatom meg a 41. diákolimpia(2000 júliusa) feladatainak megoldását?
|
|
|
| [44] Róbert Gida | 2008-07-16 16:30:30 |
 2008-as spanyolországi matematikai olimpia első napjának feladatai:
1. Legyen H egy ABC hegyesszögű háromszög magasságpontja.  A kör középpontja a BC oldalfelezőpontja, és átmegy H-n, BC oldalt A1 és A2 pontokban metszi. Hasonlóan definiáljuk a B1,B2,C1,C2 pontokat. Mutassuk meg, hogy A1,A2,B1,B2,C1,C2 egy körön vannak. A kör középpontja a BC oldalfelezőpontja, és átmegy H-n, BC oldalt A1 és A2 pontokban metszi. Hasonlóan definiáljuk a B1,B2,C1,C2 pontokat. Mutassuk meg, hogy A1,A2,B1,B2,C1,C2 egy körön vannak.
2. x,y,z valós számok mindegyike különbözik egytől és xyz=1. Mutassuk meg, hogy 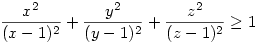 . Továbbá, hogy végtelen sok x,y,z racionális számhármasra az egyenlőtlenség egyenlőséggel teljesül. . Továbbá, hogy végtelen sok x,y,z racionális számhármasra az egyenlőtlenség egyenlőséggel teljesül.
3. Mutassuk meg, hogy végtelen sok pozitív egész n számra n2+1-nek van 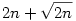 -nél nagyobb prímosztója. -nél nagyobb prímosztója.
|
|
|
