| [85] Erben Péter | 2011-07-19 21:32:23 |
 IMO2011/ 2. nap
4. feladat: Legyen n>0 egy egész szám. Van egy kétkarú mérlegünk és n súlyunk, amelyek súlya 20,21,...,2n-1. Ezt az n súlyt egymás után a mérlegre akarjuk helyezni oly módon, hogy a jobboldali serpenyő soha ne legyen nehezebb a baloldali serpenyőnél. Mindegyik lépésben kiválasztjuk az eddig a mérlegre nem tett súlyok valamelyikét, és a mérlegnek vagy a baloldali vagy a jobboldali serpenyőjébe helyezzük, egészen addig, amíg az összes súly fel nem kerül a mérlegre.
Határozzuk meg, hogy hányféleképpen lehet ezt megtenni.
5. feladat: Jelölje Z az egész számok halmazát, N pedig a pozitív egész számok halmazát. Legyen f egy Z-t N-be képező függvény. Tegyük fel, hogy bármilyen két m és n egész szám esetén az f(m)-f(n) különbség osztható f(m-n)-nel.
Bizonyítsuk be, hogy minden m,n egész számra teljesül az, hogy ha f(m) f(n), akkor f(n) osztható f(m)-mel. f(n), akkor f(n) osztható f(m)-mel.
6. feladat: Legyen ABC egy hegyesszögű háromszög,  a háromszög körülírt köre, l pedig a háromszög körülírt köre, l pedig  egy érintőegyenese. Jelölje la, lb, lc azokat az egyeneseket, amelyeket úgy kapunk, hogy l-et a BC, CA ill. AB egyenesekre tükrözzük. egy érintőegyenese. Jelölje la, lb, lc azokat az egyeneseket, amelyeket úgy kapunk, hogy l-et a BC, CA ill. AB egyenesekre tükrözzük.
Bizonyítsuk be, hogy az la, lb, lc egyenesek által meghatározott háromszög körülírt köre érinti a  kört. kört.
|
|
| [84] Erben Péter | 2011-07-19 21:28:04 |
 Szép gondolatmenet.
A végső indirekt részben az 1. esetben nem látom, miért létezik megfelelő y. Itt arról van szó, hogy A-nak nem lehet legnagyobb eleme?
Amúgy szerintem várjunk még egy kicsit a további megoldásokkal, hátha akadnak fórumozók, akik szeretnének gondolkozni a példákon.
|
| Előzmény: [83] Maga Péter, 2011-07-19 13:55:23 |
|
| [83] Maga Péter | 2011-07-19 13:55:23 |
 Egy megoldás a 3.-ra:
1. Minden valós x-re: ha f(x)<0, akkor f(x) x. Legyen ugyanis x olyan, hogy f(x)<0. Legyen y=f(x)-x. Ekkor a feltétel azt mondja, hogy f(f(x)) x. Legyen ugyanis x olyan, hogy f(x)<0. Legyen y=f(x)-x. Ekkor a feltétel azt mondja, hogy f(f(x)) (f(x)-x)f(x)+f(f(x)), 0 (f(x)-x)f(x)+f(f(x)), 0 (f(x)-x)f(x), és a negatív f(x)-szel osztva adódik az állítás. (f(x)-x)f(x), és a negatív f(x)-szel osztva adódik az állítás.
2. Minden valós x-re f(x) 0. Legyen ugyanis indirekte x olyan, hogy f(x)>0. Ekkor elég nagy abszolút értékű, negatív y-ra f(x+y) 0. Legyen ugyanis indirekte x olyan, hogy f(x)>0. Ekkor elég nagy abszolút értékű, negatív y-ra f(x+y) yf(x)+f(f(x))<0, azaz 1. szerint f(x+y)<x+y. Legyen z egy ilyen x+y, vagyis f(z) yf(x)+f(f(x))<0, azaz 1. szerint f(x+y)<x+y. Legyen z egy ilyen x+y, vagyis f(z) z, és z-nél kisebb u-ra is f(u) z, és z-nél kisebb u-ra is f(u) u. Legyen továbbá x=z+t, ahol t>0. Ekkor f(x) u. Legyen továbbá x=z+t, ahol t>0. Ekkor f(x) tf(z)+f(f(z)), itt f(f(z)) nyilván negatív, akárcsak tf(z), így f(x) is negatív, ami ellentmondás. tf(z)+f(f(z)), itt f(f(z)) nyilván negatív, akárcsak tf(z), így f(x) is negatív, ami ellentmondás.
3. Ha f(0)=0, akkor minden x 0-ra f(x)=0, azaz ebben az esetben készen vagyunk. Legyen x<0 tetszőleges. Legyen továbbá y=-x>0. Ekkor a feltétel szerint f(0) 0-ra f(x)=0, azaz ebben az esetben készen vagyunk. Legyen x<0 tetszőleges. Legyen továbbá y=-x>0. Ekkor a feltétel szerint f(0) yf(x)+f(f(x)). Itt f(f(x)) nempozitív, így 0 yf(x)+f(f(x)). Itt f(f(x)) nempozitív, így 0 yf(x), a pozitív y-nal osztva f(x) yf(x), a pozitív y-nal osztva f(x) 0, és 2.-vel összevetve adódik az állítás. 0, és 2.-vel összevetve adódik az állítás.
Tegyük tehát fel, hogy f(0)<0, ellentmondásra akarunk jutni, ezzel lennénk készen.
Osszuk két részre most a nempozitív számokat. Legyen A={x 0:f(x)=0}, B={x 0:f(x)=0}, B={x 0:f(x) 0:f(x) x}. Ekkor 1., 2., valamint az indirekt f(0)<0 feltevés értelmében A x}. Ekkor 1., 2., valamint az indirekt f(0)<0 feltevés értelmében A B a nempozitív számok egy diszjunkt felbontása. B a nempozitív számok egy diszjunkt felbontása.
Állítjuk, hogy szeletelés is, azaz a<b minden a A, b A, b B-re. Indirekte tegyük fel, hogy valamely a B-re. Indirekte tegyük fel, hogy valamely a A, b A, b B-re a>b. Ekkor x=b, y=a-b>0-t választva a feltétel azt adja, hogy f(a) B-re a>b. Ekkor x=b, y=a-b>0-t választva a feltétel azt adja, hogy f(a) (a-b)f(b)+f(f(b)). Itt a bal oldal 0, a jobb oldal pedig negatív (a-b>0, f(b)<0, f(f(b)) (a-b)f(b)+f(f(b)). Itt a bal oldal 0, a jobb oldal pedig negatív (a-b>0, f(b)<0, f(f(b)) 0), ami ellentmondás. 0), ami ellentmondás.
Innentől két esetet különböztetünk meg, mindkettőben ellentmondásra jutunk.
1. eset: A nemüres. Ekkor legyen x A, y>0 pedig olyan, hogy x+y A, y>0 pedig olyan, hogy x+y A (ilyen x,y a korábbiak szerint nyilván léteznek). Ekkor f(x+y) A (ilyen x,y a korábbiak szerint nyilván léteznek). Ekkor f(x+y) yf(x)+f(f(x)), a bal oldal 0, a jobb oldal pedig f(0), ami ellentmondás. yf(x)+f(f(x)), a bal oldal 0, a jobb oldal pedig f(0), ami ellentmondás.
2. eset: A üres. Ekkor legyen x<f(0), y=-x>0. Ekkor f(x+y) yf(x)+f(f(x)), a bal oldal f(0), a jobb oldalon yf(x) negatív, így f(0) yf(x)+f(f(x)), a bal oldal f(0), a jobb oldalon yf(x) negatív, így f(0) f(f(x)) f(f(x)) f(x) f(x) x<f(0), alkalmazva, hogy x,f(x) x<f(0), alkalmazva, hogy x,f(x) B, illetve a végén x választását. Ellentmondás. B, illetve a végén x választását. Ellentmondás.
|
| Előzmény: [82] Erben Péter, 2011-07-18 15:25:22 |
|
| [82] Erben Péter | 2011-07-18 15:25:22 |
 IMO2011 / 1. nap
1. feladat: Az A={a1,a2,a3,a4} halmaz négy, páronként különböző pozitív egész számból áll. Az a1+a2+a3+a4 összeget jelöljük sA -val, és jelölje nA az olyan (i,j) párok (1 i<j i<j 4) számát, amelyekre ai+aj osztója sA -nak. 4) számát, amelyekre ai+aj osztója sA -nak.
Határozzuk meg az összes olyan A halmazt, amelyre nA a lehetséges maximális értékét veszi fel.
2. feladat: Legyen S a sík pontjainak egy véges, legalább kételemű halmaza. Feltesszük, hogy az S halmaz semelyik három pontja sincs egy egyenesen. Egy szélmalomnak nevezett folyamat során kiindulunk egy l egyenesből, amely az S halmaznak pontosan egy P pontját tartalmazza. Az egyenes a P középpont körül az óramutató járásával megegyező irányban forog addig, amíg először nem találkozik egy másik, S halmazba tartozó ponttal. Ekkor ez a Q pont lesz az új középpont, és az egyenes a Q pont körül forog tovább az óramutató járásával megegyező irányban egészen addig, míg újra nem találkozik egy S halmazba tartozó ponttal.
Ez a folyamat vég nélkül folytatódik.
Bizonyítsuk be, hogy megválaszthatjuk a P S pontot és a P-n átmenő l egyenest úgy, hogy az S halmaz minden pontja végtelen sokszor legyen a szélmalom középpontja. S pontot és a P-n átmenő l egyenest úgy, hogy az S halmaz minden pontja végtelen sokszor legyen a szélmalom középpontja.
3. feladat: Legyen f : R R egy olyan függvény, amelyre teljesül az R egy olyan függvény, amelyre teljesül az
f(x+y) yf(x)+f(f(x)) yf(x)+f(f(x))
feltétel minden x,y valós számra. Bizonyítsuk be, hogy minden x 0 esetén f(x)=0. 0 esetén f(x)=0.
|
|
| [81] Golyoska | 2010-09-18 18:34:31 |
 Én úgy tudom, hogy ez a csapat a "kicsi IMO" csapat, azaz ez segíti felhozni a jövő bajnokait. Ez jól látható a honlapjukon: http://memo.szolda.hu helyen is, ahol az is látható, hogy az elmúlt években több olyan diák is ennek a csapatnak a tagja volt korábban, aki utána az IMO csapatban ért el szép sikereket.
Az, hogy a Kenguru verseny szervezői támogatják ezt a csapatot, az nem von le semmit sem a csapat által elért eredmény értékéből. Tudtommal rajtuk kívül (Kenguru) csak a Bolyai Társaság támogatja még őket, a minisztérium nem. Pedig az utaztatás és versenyeztetés pénzigényes ... :)
|
| Előzmény: [79] Róbert Gida, 2010-09-17 00:27:31 |
|
|
| [79] Róbert Gida | 2010-09-17 00:27:31 |
 http://index.hu/tudomany/2010/09/16/magyar_diakok_taroltak_a_kozep-europai_matekolimpian/
Az azért meglepett, hogy mindenféle ugribugri matekversenyeket is figyelembe vesznek a csapat összeállításnál.
|
|
| [78] rizsesz | 2010-07-30 12:06:18 |
 És akkor már a fizika se maradjon el:
http://ipho2010.hfd.hr/tekst.php?id=32
3 magyar arany!
|
|
| [77] rizsesz | 2010-07-22 13:33:22 |
 Művészet ennyire nem tudni csalni (már ha tényleg így történt). :) És egyben szomorú is azért, ha egy ilyen versenynél megkritizálható a tisztaság.
|
| Előzmény: [75] Python, 2010-07-22 13:08:11 |
|
|
| [75] Python | 2010-07-22 13:08:11 |
 Néhányan a 3. feladatlapra vázlatok vagy más gondolkodásra utaló jelek nélkül rögtön kimondtak egy lemmát, úgy ahogy ez a hivatalos megoldásban szerepelt, és a szóbeszéd szerint a nyitóünnepségen a csapatvezető (aki már ismerte a feladatokat és megoldásokat) egy dossziét adott át a csapatvezetőhelyettesnek (aki a verseny előtt még találkozott a diákokkal).
|
| Előzmény: [74] Blinki Bill, 2010-07-21 20:46:18 |
|
|
|
|
|
| [70] Róbert Gida | 2010-07-11 18:01:54 |
 Összesen 129 ponttal, megosztott 13. hely az országok ranglistáján. (Kína végül 197 ponttal nyert).
Bodor Bertalan: 15 pont (bronz)
Dankovics Attila: 21 pont (ezüst)
Éles András: 25 pont (ezüst)
Mészáros András: 11 pont (dicséret)
Nagy Donát: 29 pont (arany)
Nagy János: 28 pont (arany)
|
| Előzmény: [69] Láda19, 2010-07-11 12:58:37 |
|
|
|
|
| [66] Kós Géza | 2010-07-08 10:52:53 |
 Íme az idei feladatok.
Első nap
1. feladat. Határozzuk meg az összes olyan f:R R függvényt, amelyre az R függvényt, amelyre az
f([x]y)=f(x)[f(y)]
egyenlőség teljesül minden x,y R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.) R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.)
Javasolta: Franciaország
2. feladat. Legyen I az ABC háromszög beírt körének középpontja,  pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a  körrel legyen D. Legyen E a BDC körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül körrel legyen D. Legyen E a BDC körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül
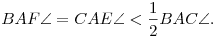
Legyen továbbá G az IF szakasz középpontja. Bizonyítsuk be, hogy a DG és EI egyenesek a  körön metszik egymást. körön metszik egymást.
Javasolta: Hong Kong
3. feladat. Legyen N a pozitív egész számok halmaza. Határozzuk meg az összes olyan g:N N függvényt, amelyre N függvényt, amelyre
(g(m)+n)(m+g(n))
teljes négyzet minden m,n N-re. N-re.
Javasolta: USA
Második nap
4. feladat. Legyen P egy pont az ABC háromszög belsejében. Az AP, BP és CP egyenesek másik metszéspontja az ABC háromszög  körülírt körével legyen rendre K, L és M. A körülírt körével legyen rendre K, L és M. A  körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML. körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML.
Javasolta: Lengyelország
5. feladat. A B1,B2,B3,B4,B5,B6 dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:
1. típusú lépés: Választunk egy Bj nemüres dobozt, ahol 1 j j 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz. 5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz.
2. típusú lépés: Választunk egy Bk nemüres dobozt, ahol 1 k k 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával. 4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával.
Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B1, B2, B3, B4, B5 dobozok mindegyike üres legyen, a B6 doboz pedig pontosan 201020102010 érmét tartalmazzon. (Definíció szerint abc=a(bc).)
Javasolta: Hollandia
6. feladat. Legyen a1,a2,a3,... pozitív valós számok egy sorozata. Tegyük fel, hogy van egy olyan s pozitív egész, amellyel
an=max {ak+an-k | 1 k k n-1} n-1}
teljesül minden n>s egészre. Bizonyítsuk be, hogy léteznek olyan  és N pozitív egészek, amikre és N pozitív egészek, amikre   s, és s, és 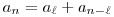 minden n minden n N-re. N-re.
Javasolta: Irán
|
|
|
|
| [63] lorantfy | 2009-07-24 16:14:38 |
 Gratulálok a csapat minden tagjának és a felkészítő tanároknak!
|
|
| [62] Python | 2009-07-23 12:32:55 |
 Gratulálok a csapatnak!
|
|
| [61] Láda19 | 2009-07-23 07:03:43 |
 Biztosak vagyunk abban, hogy mindent megtettetek az eredményes szereplés érdekében. Mnd a hatan érmet szereztetek, ez szép teljesítmény. Gratulálok a csapatnak, és mindannyiótoknak további sikeres és eredményes munkát kívánok.
|
| Előzmény: [60] janomo, 2009-07-22 20:19:23 |
|
