| [28] kdano | 2006-10-13 21:09:54 |
 Sajnos a feladatok papírját elhagytam, így nem lesz szó szerinti a feladatok szövegezése, de remélem, attól még korrekt marad:
(1) (ahogy a szomszéd GEOMETRIA topicban is olvasható):
Létezik-e olyan 2006 pontból álló halmaz a térben, amelyre igaz, hogy:
a) Nincs minden pontja egy síkban
b) Semelyik három pont sincs egy egyenesen
c) Bármely A és B ponthoz található olyan (tőlük különböző) C és D pont, hogy AB egyenes párhuzamos CD egyenessel.
(2) Legyen a,t,n egész, 1 a a n. Vegyük az {1,2,...,n} halmaz azon részhalmazait, amelyekre igaz, hogy bármely két taguk különbsége t. Bizonyítandó, hogy ezek közül az a-t nem tartalmazóak száma legfeljebb t2-szerese az a-t tartalmazók számának. n. Vegyük az {1,2,...,n} halmaz azon részhalmazait, amelyekre igaz, hogy bármely két taguk különbsége t. Bizonyítandó, hogy ezek közül az a-t nem tartalmazóak száma legfeljebb t2-szerese az a-t tartalmazók számának.
(3) Osszunk szét valahogy egy asztalt körbeülő n ember közt n-1 db kártyát. Ezek után egy lépésben egy olyan ember, akinek legalább 2 kártyája van, egy-egy kártyát ad a két szomszédjának. Bizonyítsuk be, hogy bármilyen sorrendben lépnek is, véget ér a folyamat (azaz n-1 embernél 1 kártya, egynél pedig egy se lesz)
|
|
| [27] SAMBUCA | 2006-10-12 22:32:48 |
 Üdv.
Mik voltak az idei feladatok?
Előre is köszi.
|
|
| [26] kdano | 2006-10-12 17:44:48 |
 No, és az idei kürschák hogy sikerült nektek?
Szerintem ezek a feladatok könnyebbek voltak, mint a tavalyiak, és nem csak én lettem egy évvel okosabb :P (Már csak azért is, mert az Osztályunkban minden feladatra született megoldás, holott tavaly senki nem oldotta meg az elsőt...)
|
|
| [25] cescrules | 2005-12-13 12:06:14 |
 Hello, A dicseretekrol lehet tudni valamit?
Elore is koszi, Racz Miki
|
|
|
| [23] Kós Géza | 2005-12-10 21:39:20 |
 I. díj nincs, mert senki sem oldotta meg az 1. feladatot.
II. díjat kapott Erdélyi Márton, Gyenizse Gergő, Jankó Zsuzsanna, Paulin Roland, Sümegi Károly és Szilágyi Csaba. Ők megoldották a 2. és a 3. feladatot.
III. díjat kapott Magda Gábor, Nagy Csaba és Seres Gyula. Ők is lényegében megoldották a 2. és a 3. feladatot, de a dolgozataikban voltak kisebb pontatlanságok, amik miatt a megoldásuk nem teljes.
|
| Előzmény: [22] Doom, 2005-12-10 17:32:22 |
|
| [22] Doom | 2005-12-10 17:32:22 |
 Tudja már vki, mik lettek az idei eredmények?
|
|
|
|
|
| [18] lorybetti | 2005-10-10 08:09:24 |
 Valaki nem tenné meg, hogy beírja az idei feladatokat?
Sokan megköszönnék...(szierintem, köztük jómagam is)
|
|
| [17] Sümegi Károly | 2005-10-09 16:12:59 |
 Üdvözlöm az oldal olvasóit! Milyen nehezek voltak az idei feladatok? Én az utolsó 2 feladattal foglalkoztam.
|
|
| [16] KiCsa | 2005-10-07 20:43:32 |
 A 2005. évi Kürschák József Matematikai Tanulóverseny feladatai
1. feladat:
Legyen N>1 és legyenek a1,a2,...,aN olyan nemnegatív valós számok, amelyek összege legfeljebb 500. Bizonyítandó, hogy létezik olyan k 1 egész szám és léteznek olyan 1=n0<n1<...<nk=N egészek, amelyekre teljesül, hogy 1 egész szám és léteznek olyan 1=n0<n1<...<nk=N egészek, amelyekre teljesül, hogy
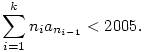
2. feladat:
A és B teniszeznek. Az a játékos győz, aki elsőként nyer meg legalább négy labdamenetet úgy, hogy ellenfelénél legalább kettővel több labdamenetet nyert. Tudjuk, hogy az A játékos minden labdamenetet, a korábbiaktól függetlenül, p 1/2 valószínűséggel nyer meg. Bizonyítsuk be, hogy az A játékos győzelmének valószínűsége legfeljebb 2p2. 1/2 valószínűséggel nyer meg. Bizonyítsuk be, hogy az A játékos győzelmének valószínűsége legfeljebb 2p2.
3. feladat:
2×1-es dominókból tornyot építünk a következő módon. Először elrendezünk 55 dominót úgy, hogy egy 10×11-es téglalapot fedjenek le; ez lesz a torony első szintje. Erre azután további, 55 dominót tatalmazó szinteket építünk, ügyelve arra, hogy minden egyes szint pontosan illeszkedjék az előzőre. Az így kapott építményt akkor nevezzük stabilnak, ha a 10×11-es téglalap minden rácsponttól különböző, belső pontja felett van dominónak belső pontja. Hány szintből áll a legalacsonyabb stabil torony?
|
|
|
| [14] Doom | 2005-09-28 21:17:48 |
 Bp-en a BME Informatikai épület IB028 sz. előadótermében (Bp, XI. Magyar Tudósok krt. 2.)
Máshol is van, ha esetleg nem bp-en laksz... :P
|
| Előzmény: [13] KiCsa, 2005-09-28 19:44:10 |
|
|
|
| [11] KiCsa | 2005-09-28 17:43:01 |
 Pontosan mikor és lesz az idei Kürschák?
|
|
| [10] KiCsa | 2004-11-23 20:12:34 |
 Fel is lettek rakva a diák, itt megtalálhatod. A Kürschák 3. feladat általánosítása a diákon a 7. feladatként szerepel. Sajnos néhány dia elég lassan töltődik be, mert az ábrák mind háttérképként vannak, így ha valakinek egy diára kattitntva csak két-három betű jelenne meg, akkor csak várjon türelmesen :-). Sajnos egyes matematikai karakterek nem jelennek meg jól minden böngészőben, de nincs túl sok ilyen (néhány unió stb.).
|
| Előzmény: [9] Csimby, 2004-11-15 19:34:04 |
|
| [9] Csimby | 2004-11-15 19:34:04 |
 Az Ankéton a gráfos előadáson elhangzott egy gráfos megoldás a 3. feladatra. Sajnos én akkor iszonyatosan álmos voltam, és ezért nem emlékszem rá, de ha valaki emlékszik, szerintem érdemes lenne beírni. Egyébként asszem az előadó azt mondta, hogy az előadás teljes anyaga fel lesz rakva a KöMaL honlapjára.
|
|
| [8] Kós Géza | 2004-10-29 10:53:20 |
 Erben Péter hívta fel rá a figyelmemet, hogy majdnem ugyanez volt az 1978-as olimpia 4. feladata:
Az ABC háromszögben AB=AC. Egy kör belülről érinti az ABC háromszög köré írt kört, továbbá az AB oldalt a P, az AC oldalt a Q pontban. Bizonyítsuk be, hogy a PQ szakasz felezőpontja az ABC háromszög beírt körének középpontja.
|
| Előzmény: [7] Kós Géza, 2004-10-29 10:47:15 |
|
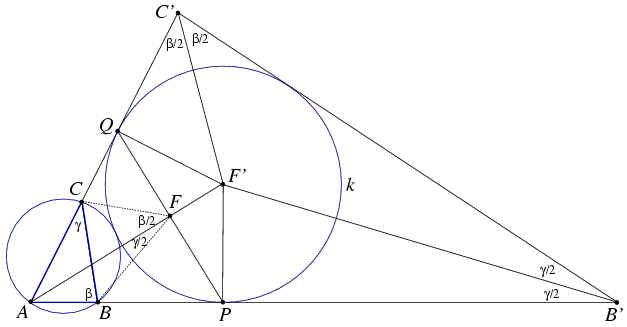
| [7] Kós Géza | 2004-10-29 10:47:15 |
 Van egy rövid inverziós megoldás is.
Alkalmazzunk inverziót az A középpontú, AP=AQ sugarú körre. A B, C, F pontok képe legyen B', C', illetve F'. A k kör képe önmaga, a körülírt kör képe a B'C' egyenes, ezek szintén érintik egymást.
A befogótételből következik, hogy F' éppen a k kör középpontja.
Az ABC és AC'B' háromszögek hasonlók, innen AB'C' = = és AC'B' és AC'B' = = . Az AB'C' háromszögben k éppen a beírt kör, tehát B'F' és C'F' szögfelezők. . Az AB'C' háromszögben k éppen a beírt kör, tehát B'F' és C'F' szögfelezők.
Az ABF és AF'B' , illetve ACF és AF'C' háromszögek is hasonlók, így 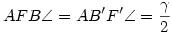 és és 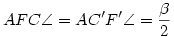 . .
Az ABF és ACF háromszögek szögeit összeszámolva kapjuk, hogy BF és CF éppen az ABC háromszög külső szögfelezői.
|
 |
| Előzmény: [5] Kemény Legény, 2004-10-28 16:59:30 |
|
| [6] Kós Géza | 2004-10-29 10:18:33 |
 A 3. feladat valószínűleg onnan származik, hogy valaki transzformációk szorzatával játszott.
A pontok jelentsék a sík geometriai transzformációit, nevezetesen a kék pont jelentsen tükrözést az x-tengelyre, a piros pont pedig jelentsen origó körüli, 120o-os forgatást. Minden egyes helyzetben szorozzuk össze, avagy alkalmazzuk egymás után a transzformációkat a teljes körön.
Két kék pont esetén a szorzat mindig az identitás, akárhonan kezdjük a transzformációkat összeszorozni és ez a tulajdonság minden lépésnél megmarad.
Két piros pont esetén viszont a szorzat nem az identitás. A két kék pontból indulva tehát nem lehet a két piros pontot elérni, és fordítva.
A megoldás elmondható transzformációk nélkül is, ahogy azt már láttuk. A kék pontok száma mindig páros, és a kört páros sok ívre osztják. Ha minden második íven megszámoljuk a piros pontokat, és minden elsőn is, a kétféle összeg különbsége 3-mal osztva vagy mindig 0, vagy mindig  1 maradékot ad. 1 maradékot ad.
|
| Előzmény: [4] BohnerGéza, 2004-10-28 14:25:12 |
|
| [5] Kemény Legény | 2004-10-28 16:59:30 |
 Az 1. feladatra gyors megoldás adható Casey tételének segitségével.Casey tétele:Adott egy k kör és 4 másik kör (k(1),k(2),k(3),k(4)),amelyek érintik a k kört.Ekkor e(12)e(34)+e(23)e(41)=e(13)e(24) ,ahol e(ij) az a k(i) és a k(j) körök közös érintőszakaszának a hossza,mégpedig a külső érintőt kell venni,ha a két kör k ugyanazon oldalán van.egyébként pedig a belső érintőszakaszt kell venni.(Ez a Ptolemaiosz-tétel egyfajta általánositása is).A Kürschák-feladatban pedig 3 pontkör van(a 3 csúcs),ill.a megadott speciális tulajdonságú kör,az alapkör pedig a köréirt kör.Az érintőszakaszok számolhatóak a Casey-tételből,igy AP hossza könnyen meghatározható a háromszög oldalaiból.Innen pedig már egyszerü a befejezés...
|
|
| [4] BohnerGéza | 2004-10-28 14:25:12 |
 A harmadik feladat megoldásával a Nehezebb matematikai problémák téma [96.], [103.] és [104.] hozzászólása foglalkozik.
|
|
