Fórum - Kürschák-verseny

Ahogy a téma elején is megtették, tudna valaki ide megoldásokat írni? Az is jó, ha behivatkoztok egy weboldalt, ahol megtaláljuk. (VersenyVizsgán megvan 2008-ig.)

Valaki el tudná küldeni bármelyik feladatnak a megoldását? Nagyon hálás lennék érte! Előre is köszönöm! bkovacs0130@gmail.com

Köszönöm!

1.Az ABC háromszög A-val, illetve B-vel szemközti hozzáírt körének középpontjait jelölje J(A), illetve J(B). Húzzuk meg a körülírt kör egy olyan PQ húrját, amely párhuzamos az AB oldallal, továbbá metszi az AC és BC oldalszakaszokat.Az AB és CP egyenesek metszéspontja legyen R.Bizonyítsuk be, hogy J(A)Q J(B)szög+J(A)RJ(B) szög=180 fok.

2.Jelölje E(n) az n pozitív egész szám 2-es számrendszerbeli felírásában az 1-esek számát. Nevezzünk egy n pozitív egész számot érdekesnek, ha n osztható E(n)-nel.Bizonyítsuk be, hogy a)nem lehet 5 egymás utáni pozitív egész szám mindegyike érdekes, továbbá, hogy b)végtelen sok olyan n pozitív egész szám van,amelyre az n, n+1 és n+2 számok mindegyike érdekes.

3.Tekintsünk n eseményt, amelyek mindegyikének valószínűsége 1/2, továbbá bármelyik kettő együttes bekövetkezésének valószínűsége 1/4. a) Igazoljuk,hogy annak a valószínűsége, hogy egyik sem következik be, legfeljebb 1/(n+1). b)Mutassuk meg, hogy végtelen sok olyan n természetes szám létezik, amelyre megadhatók az események oly módon, hogy pontosan 1/(n+1) legyen annak a valószínűsége, hogy egyik sem következik be.

Az idei feladatokat fel tudná tenni valaki? Köszönöm előre is!

Köszi :)

2010:

1. Adott n lezárt bőrönd és n kulcs úgy, hogy a bőröndök mindegyikét pontosan egy kulcs nyitja és mindegyik kulcs pontosan egy bőröndöt nyit. Célunk az, hogy az összes bőröndről megállapítsuk, melyik kulcs nyitja. Egy próbálkozás abból áll, hogy valamelyik kulccsal megpróbálunk kinyitni egy bőröndöt. Határozzuk meg azt a legkisebb p(n) számot, melyhez létezik olyan eljárás, hogy azt végrehajtva legfeljebb p(n) próbálkozás után bizonyosan ismerni fogjuk az n összetartozó bőrönd-kulcs párt.

2. Az ABC háromszög AB oldalának belsejében adottak a C₁ és C₂ pontok, a BC oldal belsejében az A₁ és A₂ pontok, végül a CA oldal belsejében a B₁ és B₂ pontok úgy, hogy AC₁<AC₂, BA₁<BA₂, és CB₁<CB₂ teljesül. Az AB₁C₁ és AB₂C₂ körök A-tól különböző metszéspontját jelölje A*, a BC₁A₁ és BC₂A₂ körök B-től különböző metszéspontja legyen B*, végül a CA₁B₁ és CA₂B₂ körök C-től különböző metszéspontját nevezzük C*-nak. Mutassuk meg, hogy az AA*, BB* és CC* egyenesek egy ponton mennek át.

3. Mely n és k pozitív egész számokra léteznek a₁, a₂,..., a_n, b₁, b₂,..., b_k egész számok úgy, hogy az a_ib_j szorzatok (1in, 1jk) páronként különböző maradékot adnak nk-val osztva?

Valaki fel tudná tenni az idei példákat?

2009:

1. Egy n×k-as táblázatba úgy írunk be egész számokat, hogy mind az n sorban szerepeljen 1-től k-ig minden egész szám. Jelöljük S-sel a kapott k oszlopösszeg legnagyobbikát. Minden n-re és k-ra adjuk meg S lehetséges legkisebb értékét!

2. Határozzuk meg azokat a pozitív egészekből álló (a,b) számpárokat, amelyekre igaz az alábbi állítás: a pozitív egészek halmaza felbontható két diszjunkt halmaz, H₁ és H₂ uniójára úgy, hogy sem a, sem b nem írható fel sem két H₁-beli, sem két H₂-beli szám különbségeként.

3. Határozzuk meg azokat az f függvényeket, amelyekre

(i) f az egész számok halmazán van értelmezve;

(ii) f(z) racionális szám minden z egész szám esetén;

(iii) ha f(x)<c<f(y) és c racionális, akkor f felveszi a c értéket; és

(iv) ha x,y,z egészek és összegük nulla, akkor f(x)+f(y)+f(z)=f(x)f(y)f(z) teljesül.

1.feladat. Jelölje az n pozitív egész szám pozitív osztóinak számát d(n). Melyik az a legkisebb valós c érték, amellyel 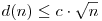teljesül minden pozitív egész számra?

2.feladat. Legyenek n1 és a₁<a₂<...<a_n egészek. Biz. be, hogy azoknak az 1i<jn pároknak a száma, amelyekre a_j-a_i kettőhatvány, legfeljebb akkora, mint azoknak az 1i<jn pároknak a száma, amelyekre j-i kettőhatvány.

3.feladat. Egy országban a városok közötti közlekedés vonaton és busszal lehetséges. A vasúttársaság és a buszvállalat is bizonyos várospárok között közlekedtet járatokat, ám két város között nem feltétlenül jár mindkét irányba járat. Tudjuk, hogy bárhogyan is választunk ki két várost, el lehet jutni egy fajta közlekedési eszközön (esetleges átszállásokkal) az egyikből a másikba(de a másikból az egyikbe már nem feltétlenül). Biz. be, hogy van olyan város, amelyből bármely másik város elérhető egyféle közlekedési eszközzel úgy, hogy a különböző városokba jutás eszköze más-más lehet.

I.díj: Lovász László Miklós, II.díj: Nagy János.

Oké :) kik a díjazottak :)?

Sajnos nincsen olyanom, amúgy tudom. :)

A Kömal 2009/2 számában.

Sziasztok!

A 2008. évi verseny feladatai, illetve eredményei elérhetőek valahol?

Mikor lesz meg, hogy kit hívnak meg az eredményhirdetésre?

Azt tudom, de kíváncsi voltam, hogy ez jó-e, sajnos nem :-(

Na mindegy

Ennek a feladatnak spec ott van a megoldása a GEOMETRIA topicban..

Sajnos nem jó, mivel az 1003 páratlan. Első gondolatom nekem is ez volt. De ekkor ez nem lehetne ezen a versenyen feladat. Két év múlva egyébként jó lenne a megoldás, aztán négyévente.

Ellenpélda: Legyenek Ai-vel, illetve megfelelően Bi-vel (i=1, 2, 1003) jelölve a két szabályos sokszög csúcsai. ekkor pl. az A1B2- höz (általában) nincs párhuzamos szakasz.

Veszel két db szabályos 1003 szöget, úgy, hogy a két lap egymás eltolt képe, de nincsenek egy síkban. Ez nyilván megadható, és a feladatnak is eleget tesz szerintem. Ha nem jó, ekkor bocs...

De igen :P Bármely két elemének különbsége legalább t. Sorry for that :P

nem úgy volt, hogy "legalább t"? bocs ha rosszul emlékszem :)

Ne haragudj, de a 2. feladatot nem értem. "Bármely két taguk különbsége t" mit akar jelenteni?

Sajnos a feladatok papírját elhagytam, így nem lesz szó szerinti a feladatok szövegezése, de remélem, attól még korrekt marad:

(1) (ahogy a szomszéd GEOMETRIA topicban is olvasható):

Létezik-e olyan 2006 pontból álló halmaz a térben, amelyre igaz, hogy:

a) Nincs minden pontja egy síkban

b) Semelyik három pont sincs egy egyenesen

c) Bármely A és B ponthoz található olyan (tőlük különböző) C és D pont, hogy AB egyenes párhuzamos CD egyenessel.

(2) Legyen a,t,n egész, 1an. Vegyük az {1,2,...,n} halmaz azon részhalmazait, amelyekre igaz, hogy bármely két taguk különbsége t. Bizonyítandó, hogy ezek közül az a-t nem tartalmazóak száma legfeljebb t²-szerese az a-t tartalmazók számának.

(3) Osszunk szét valahogy egy asztalt körbeülő n ember közt n-1 db kártyát. Ezek után egy lépésben egy olyan ember, akinek legalább 2 kártyája van, egy-egy kártyát ad a két szomszédjának. Bizonyítsuk be, hogy bármilyen sorrendben lépnek is, véget ér a folyamat (azaz n-1 embernél 1 kártya, egynél pedig egy se lesz)

Üdv.

Mik voltak az idei feladatok?

Előre is köszi.