KöMaL: English issue, December 2002

	English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solutions of advanced problems A

A. 269. A circular hole is to be completely covered with two square boards. The sides of the squares are 1 metre. In what interval may the diameter of the hole vary?

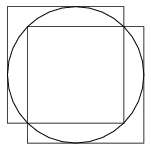
Figure 1

It is easy to see that a hole of radius $\displaystyle 2-\sqrt2$ (and all smaller holes) can be covered by two unit squares, see Figure 1.

We will prove that if a unit square covers at least half of the perimeter of a circle of radius r, then $\displaystyle r\le2-\sqrt2$. This implies that the diameter of the hole cannot exceed

$\displaystyle 4-2\sqrt2\approx1.17~\rm metre. $

Let K be a circle of radius r, and N be a unit square, which covers at least the half of K. If r$\displaystyle \ge$1/2, then N can be translated such that each side of N or its extension has at least one common point with K and the covered part of the curve is increasing, see Figure 2.

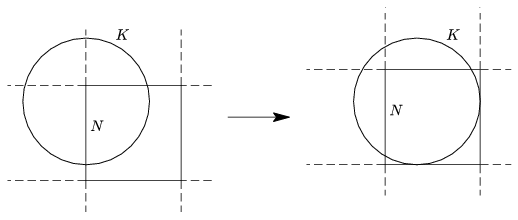
Figure 2

So, it can be assumed that r>1/2 and (the extension of) each side of N has a common point with K.

First, assume that a vertex of N is inside K. Let the vertices of N be A, B, C, D and suppose that A is inside K. Denote the intersection of K and the half-lines AB and AD by P and Q, respectively. (Figure 3.)

Because PAQ$\displaystyle \angle$=90^o, the centre of K and vertex A are on the same side of line PQ. This implies that the uncovered arc PQ is longer than the half of K. This is a contradiction, thus this case is impossible.

We are left to deal with the case when there are no vertices of N inside K and each side or its extension has a common point with K. It is easy to check that these common points cannot be on the extension of the sides of N; they must lie on the perimeter of N.


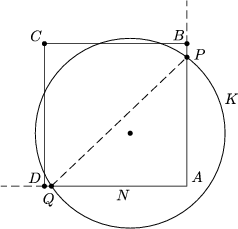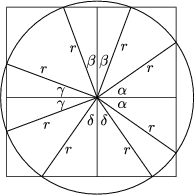Figure 3	Figure 4

Denote by $\displaystyle \alpha$, $\displaystyle \beta$, $\displaystyle \gamma$ and $\displaystyle \delta$ the angles drawn on Figure 4.

The total of the uncovered arcs is at most the half of K, so $\displaystyle \alpha$+$\displaystyle \beta$+$\displaystyle \gamma$+$\displaystyle \delta$ $\le$ 90^o. By symmetry, it can be assumed that $\alpha$ + $\gamma$ $\le$ 45^o.

As can be read from the Figure, r(cos $\alpha$ +cos $\gamma$ )=r(cos $\beta$ +cos $\delta$ )=1. The concavity of the cosine function yields

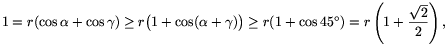
$1=r(\cos\alpha+\cos\gamma)\ge r\big(1+\cos(\alpha+\gamma)\big)\ge r(1+\cos45^\circ)=r\left(1+\frac{\sqrt2}{2}\right),$

and hence 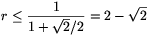$r\le\frac{1}{1+\sqrt2/2}=2-\sqrt2$ .

Thus, the radius of the hole can be at most 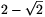$2-\sqrt2$ ; its diameter can be at most 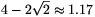$4-2\sqrt2\approx1.17$ metre.

Already signed up?
New to KöMaL?

English Issue, December 2002

Solutions of advanced problems A