English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solution of the problems for information technology November 2001

I. 8. A dog swims across the river, always heading for its trainer standing on the opposite riverside. The approximate path of the dog in the river is to be modelled and displayed on the screen. One should be able to input the following real parameters from the keyboard:

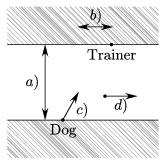
a) the width of the river in meters

b) the distance (in meters) of the trainer from the starting position of the dog projected onto the opposite riverside. (The distance is positive if it is in the same direction as the streamline of the river and negative otherwise.)

c) the constant velocity of the dog (in \(\displaystyle \rm\frac{m}{s}\)).

d) the constant velocity of the river (in \(\displaystyle \rm\frac{m}{s}\)).

e) the accuracy of approximation, that is the length of the time interval (in seconds) in which your program can replace the actual motion by a straight line segment.

The two riversides are considered as parallel lines. Simulation should stop when the dog has approached the opposite riverside within 1 meter.

The dog's motion depends on its direction, its velocity and the river velocity. Remember that these are constant velocities. However, the direction of the motion and the x- and y-components of the dog's velocity (depending on its direction) can be considered constant only in a time interval. The dog's direction can be computed by the following formula:

Draw the two sides of the river as parallel lines, the starting position of the dog and the trainer, and the path of the dog derived from the above formulation.

(10 points)

Solution. Displaying this simulation uses a simple conversion between the real system of coordinates and the axes on the computer screen. On pixel corresponds to 1 meter, and values along the x-axis increase rightwards, while values along the y-axis increase - counter to the usual case - downwards. Explanation of the code.

The variables according to the original problem read as follows. The riversides are drawn. One did not need to draw the velocity vector, so it is drawn now in blue, then red colour is set back.

The new x- (and the y-components also) can be computed by considering a straight and uniform motion and the formula given in the Problem.

We draw a straight line to the new coordinates. The time elapses in the small interval.

The result is displayed.

The Pascal program implements our algorithm is finding on http://www.komal.hu/verseny/2001-11/I.e.shtml.