English Issue, December 2002
	Previous page	Contents	Next page	ORDER FORM

Solutions of problems for physics P

M. 222. The angle of refraction of a puck bouncing back from a board is usually not identical to its angle of incident. (The motion of a puck can be modelled using the lid of a jar.) How does the angle of refraction depend on the speed of the puck (lid) and on the angle of incidence?

Solution. For an adequate measurement one needs a `puck launching device' which can repeat puck launches at the same initial speed (within measurement error). This technical problem was resolved by most competitors, using a spring or rubber operated `catapult'. Biró István (10th form student of Bolyai Farkas Secondary School, Marosvásárhely) constructed a clever device, which, in addition to the repeatable launches, solved the problem of recording the path of the puck (Fig. 1). He bore a hole into the middle of the puck, into which he put a toothpick wrapped in sewing thread. He had black ink permeated into the thread, and so the end of the sewing thread, just touching a glass plate, draw the path of the centre of mass of the puck.

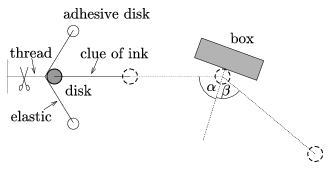
Figure 1

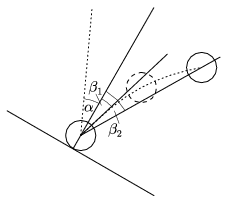
Figure 2

Two competitors, Nagy Ádám (12th form student of Szent István Secondary Grammar School, Budapest) and Biró István, noticed that the reflected path of the puck `bends', but they did not use this fact in the determination of the reflection angle. All of the competitors calculated the \(\displaystyle \beta\)₂ reflection angle from the position of the puck after it had stopped, but this differs slightly from angle \(\displaystyle \beta\)₁ which characterizes the collision better though it is more difficult to measure (Fig. 2).

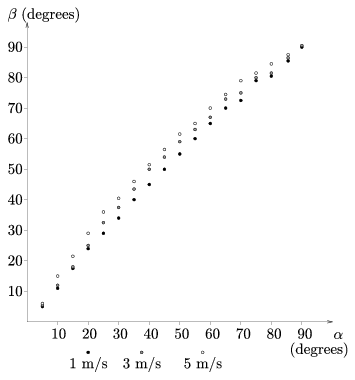
Figure 3

A crucial point in the completion of the measurement is the selection of the sliding surface. Most competitors chose a smooth surface. In the velocity measurement they had to take friction into account. Jurányi Zsófia (12th form student of Leöwey Klára Secondary Grammar School, Pécs) carried out her measurements on a panel board oiled with co-oking oil. She stated that on a board like that friction is negligibly small. Geresdi Attila (11th form student of Árpád Fejedelem Secondary Grammar School, Pécs) made his experiments on a 1 m² air-cushioned table. The competitors usually used rulers and bevels for measuring the angles, but there were other methods as well: Sükösd Zsuzsanna (7th form student of Orsolya Rendi Szent Angéla Elementary and Secondary Grammar School, Budapest,) used `chequered' floor-plates as a co-ordinate system to define the position and the motion of the puck. Almost all the competitors got a result where the reflection angle was greater than the angle of incidence, but the difference was small and decreased while approaching the perpendicular direction. This was demonstrated by the graph drawn by Szilágyi Péter (9th form student of Kossuth L. Secondary Grammar School, Debrecen) containing the data for 3 different velocities (Figure 3). Nagy Ádám plotted the ratio of the reflection and incidence angles as a function of the incidence angle (Figure 4).

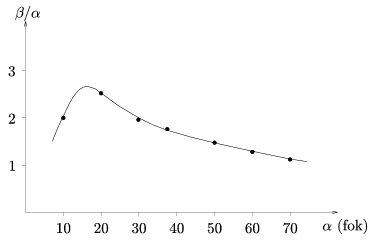
Figure 4

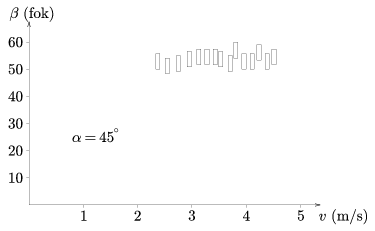
Figure 5

The experimental examination of velocity dependence is more difficult than measuring the angles. Using slopes the attainable velocity differences of the pucks started from different heights are not big enough - with considerable measurement errors - to find a definite connection between the angles and velocities. (Using catapult devices the velocity of the impact can be greater, but the measurement of velocity becomes more inaccurate.) The data measured by Jurányi Zsófia is shown in Figure 5. She plotted the \(\displaystyle \beta\) reflection angle (the accuracy of the measurement is also indicated) against different v impact velocities at fixed \(\displaystyle \alpha\)=45^o incidence angle. It can be seen that in the investigated interval \(\displaystyle \beta\) is independent of v.