 | English Issue, December 2002 | |||
| Previous page | Contents | Next page | ORDER FORM | |
Poncelet's theorem
András Hraskó
The prisoner
J. V. Poncelet, a 24-year-old soldier of Napoléon was taken prisoner by Kutuzov's army while retreating from Moscow. In the severe winter of 1812-13, he and his fellows were marched 800 km across the Russian steppe to the prisoner camp of Saratov. In captivity, Poncelet recalled his studies completed recently, and the memories started to live a new life in his mind. With no access to a library, without any spiritual companion and tormented by physical pain, the young military engineer discovered new areas of geometry. He developed the concept of ideal points, he dreamed about a special mapping called polarity, and polygons were dancing around in his mind. Poncelet's theorem, the topic of this article, was also born there.
The prisoners who survived, including Poncelet, were released in the September of 1814. The engineer-mathematician's thoughts bred in captivity were published in 1822. His book was called ``Treatise on the Projective Properties of Figures.'' The following theorem is from that book.
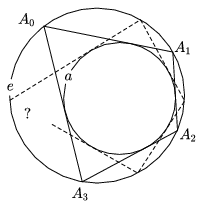
Figure 1
Poncelet's Theorem: Let the circle a lie in the interior of a circle e, not touching it. Starting at an arbitrary point A0 on e, the points A1,A2,... of circle e can be successively constructed, such that the chords A0A1,A1A2,... are all tangent to the circle a, and any two consecutive lines should be different.
It may happen that we get back to A0 in a finite number of steps, that is, An=A0. In that case, we always end up at the starting point, no matter how it is chosen on the circle e, and the number of steps required will always be the same (n).
The theorem does not claim that this will always happen, but that whether or not we will get back depends on the size and mutual position of the two circles only and not on the particular choice of the starting point.
For concentric circles, the statement is obvious. In the general case, however, the proof is quite complicated. This innocent-looking theorem is not only interesting because of its romantic birth, but also because it leads us into the thick of 19th-century mathematics. Poncelet's result, to be stated in its general form two chapters below, is equivalent to the group property of cubic curves and to the addition theorems of elliptic functions, the generalizations of trigonometric functions.
Poncelet did formulate his theorem for arbitrary irreducible second order curves (see Problem 6) rather than circles. It is unnecessary for one curve to be inside the other one, but that kind of generalization would make the elementary treatment very difficult.
Pencils of circles
The (affine) equation of a circle a of radius r1 centered at Oa(ua,va) is
| (1) | (x-ua)2+ (y-va)2- ra2=0. |
Let a(x,y) denote the polynomial on the left-hand side as a function of x and y. If a point P(\(\displaystyle \xi\),\(\displaystyle \eta\)) lies on this circle then
a(\(\displaystyle \xi\),\(\displaystyle \eta\))=0,
and if not, then
a(\(\displaystyle \xi\),\(\displaystyle \eta\))\(\displaystyle \ne\)0.
In the latter case, the value of a(\(\displaystyle \xi\),\(\displaystyle \eta\)) not only shows that P does not lie on the circle, but also the way it does not lie on it.
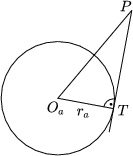 | 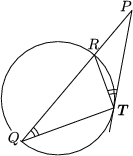 | 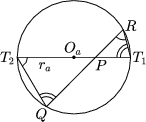 |
| OaP2-ra2=PT2 | PR.PQ=PT2 | PR.PQ= PT1.PT2= OaP2-ra2 |
| Figure 2 | ||
The part (\(\displaystyle \xi\)-u1)2+ (\(\displaystyle \eta\)-va)2 of the expression a(\(\displaystyle \xi\),\(\displaystyle \eta\)) computes the square of the length of segment OaP. If a(\(\displaystyle \xi\),\(\displaystyle \eta\)) is negative, it means that OAP2<ra2, that is, P lies in the interior of the circle a. If it is positive, then P lies outside the circle and a(\(\displaystyle \xi\),\(\displaystyle \eta\)) is equal to the square of the tangent drawn to the circle from P (Figure 2).
We can say a little more that that. It is true in both the positive and the negative case that for all secants drawn to the circle from P intersecting the circle at R and Q, the value of PR.PQ is constant, that is, independent of the choice of the secant. This can be proved with the help of similar triangles arising from the equal angles subtended by the chord at the points of a segment of a circle and the angle enclosed between the chord and the tangent drawn at its endpoints.
This constant value1 of PR.PQ is also called the power of the point P with respect to the circle a, and it is equal to OaP2-ra2= a(\(\displaystyle \xi\),\(\displaystyle \eta\)).
Thus we can say that the equation
a(x,y)=t
is satisfied by those points whose power with respect to the circle a is t. For t>0, these are the points for which the square of the tangent is t.
Let b be a circle different from a, with the equation
b(x,y)= (x-ub)2+ (y-vb)2- rb2=0.
Consider the points for which the ratio of the tangents drawn to a and b is constant. Generally speaking, let c be the locus of those points in the plane whose power with respect to a and power with respect to b are in the ratio \(\displaystyle \alpha\) to \(\displaystyle \beta\). The equation of the set c is
| (2) | \(\displaystyle \beta\)a(x,y)- \(\displaystyle \alpha\)b(x,y)=0. |
This equation also represents a circle (or a point, or the empty set, or a line if \(\displaystyle \alpha\)=\(\displaystyle \beta\)), as it is an equation in two variables where the coefficients of x2 and y2 are equal (zero if \(\displaystyle \alpha\)=\(\displaystyle \beta\)) and there is no term in xy.
The set of curves of the form (2) is called the pencil generated by a and b. From any two elements of the pencil, every element can be obtained by means of a linear combination. Thus the pencil is generated by any two of its elements, that is, any two elements determine the system.
If a and b are two arbitrary circles of the pencil, and c is any element of the system, then the ratios of the powers of all points of c with respect to a and are the same.
Figure 3
It is not hard to show that there are three kinds of pencils of circles: non-intersecting, touching and intersecting. In the first case, no two circles of the system share a common point, in the second case all the circles touch at one point, and in the third case they all pass through two common points. (See also Problems 1 and 2.)
Poncelet's reasoning
In this chapter, there will be very little proof, it is rather an outline of Poncelet's reasoning. All the more, so, as the proof of the last chapter will also shed light to some of the details here.
A famous theorem by L. Euler establishes a relationship between the radii r and R of the inscribed and circumscribed circles of a triangle and the distance d of their centres:
| (3) | R2-d2=2Rr. |
The proof can be found in Geometry Revisited by H. S. M. Coxeter and S. L. Greitzer (Theorem 2.1.2), but Problem 3 also provides some help.
Assume now that the task is to construct a triangle, given the radii of the circumscribed and inscribed circles and the distance between their centres. It follows from the theorem that if the three data do not satisfy condition (3) then there is no such triangle but there are infinitely many solutions if they do.
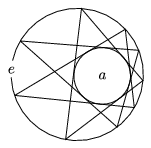
Figure 4
This is similar to constructing a triangle when the three angles are given. The solution only exists if the sum of the angles is 180o, but then there are infinitely many of them. In the latter case, one can even choose one side of the triangle arbitrarily, and still get a solution. Similarly, if the radii R and r of the circles e and a satisfy equation (3), then any point of e can be chosen as one vertex of the triangle circumscribed about a. Obviously, this statement requires a proof, see Problem 3 for a hint. From the statement and Euler's theorem, Poncelet's theorem follows for n=3: the polygon will only close up in three steps if the condition (3) holds, but then it will close up wherever the starting point is.
Let us investigate how the ``imaginary'' triangles corresponding to data not satisfying equation (3) fail to exist. The steps of Poncelet's proof and the way he complains about the lack of constructing tools in the foreword of his book suggest that this was the question the imprisoned engineer wanted to answer.
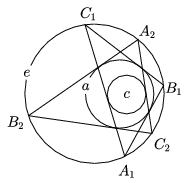
Figure 5
Figure 5 shows an attempt to construct a triangle when the data are inconsistent. The circles e and a correspond to such a situation. From an arbitrary point A of the circle e, a tangent is drawn to a. The tangent intersects e at the next vertex B of the triangle. C is obtained by drawing the other tangent to a from B. As the line AC does not touch a, it is clear that the construction was not successful. After a number of similar attempts, Poncelet must have noticed (as that is what he has proved) that although none of the lines AC obtained by the construction touch the circle a, they all do touch a certain other circle c. What is more, this circle c belongs to the pencil generated by e and a. This is particularly apparent in the case of intersecting circles a, e, when the construction of the triangle is obviously hopeless.
Thus the triangles do not exist ``by following a very regular pattern.'' It has turned out that beyond triangles and their two circles Euler's theorem has also something to say about the polygon that snakes its way between the circles of a pencil.
The observations lead to the following generalization of the above construction problem:
Let a given circle e and the circles a, b, c in its interior all belong to the same pencil. Construct a triangle, such that its circumscribed circle is e, and its sides AB, BC, AC touch that the circles a, b, c, respectively.
There are two tangents to a circle from an exterior point. In order to eliminate the ambiguity as to which tangent to draw in the construction, let us define a fixed sense of rotation for each of the circles a, b, c, and require that the directions of \(\displaystyle \overrightarrow{AB}\), \(\displaystyle \overrightarrow{BC}\), \(\displaystyle \overrightarrow{CA}\) on the sides of the triangle ABC to be constructed should all have the same orientation that the circles they touch.
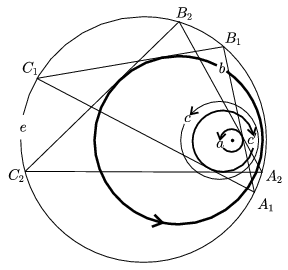
Figure 6
The solution of the construction problem is similar to that of the above problem, but now the proof is even more difficult. As before, the difficulty does not lie in the construction itself, but in the discussion of whether there are solutions in various cases: For appropriate circles e, a, b, c (and appropriate orientation on a, b, c) the construction will always produce a unique triangle, whichever point of e is chosen as a starting point. In general, furthermore, one can notice again that the lines AC always touch a certain element c' of the pencil, and they always touch it in the same orientation. This circle c', however, is different from the given c in most of the cases. Now we are not investigating when does this circle c' coincide with c, as it is surprising enough that such a c' should exist at all.
Consider now the mapping defined on the set of points of the circle e that maps the point X\(\displaystyle \in\)e onto the point where the tangent drawn from X in the appropriate direction to the (directed) circle a intersects the circle e again. If the circle a coincides with e, then this mapping is defined to be the identity that maps the points of e onto themselves. If they are concentric but not identical, the mapping is a simple rotation. In any other case, it is not a rotation, only similar to it. That kind of mapping is called an ``oblique rotation''. The composition of two consecutive rotations about the same point is equivalent to a single rotation through an angle equal to the sum of the two angles of rotation.
According to the above observation, the first part of this statement can be generalized: The composition of the oblique rotations with respect to the directed circle a and then with respect to the directed circle b is also an oblique rotation, the one determined by the circle c' above. Jacobi's proof will show what is the number, or measure that corresponds to the angle of rotation in the general case. As if on the set \(\displaystyle \mathbb{P}\) comprising the circle e and the oriented circles of the pencil lying in its interior, including the one point circle (see Problem 2) there were an operation \(\displaystyle \circledast\) that corresponds to the composition of oblique rotations:
\(\displaystyle a\circledast b=c'. \)
What Poncelet actually did, although he did not even mention such abstract algebraic concepts, was to show that this operation was associative and commutative. Thus the set \(\displaystyle \mathbb{P}\) is a commutative group, in other words an Abelian group, with respect to the above operation, as the remaining group axioms also hold: e is the identity element, and the inverse of a given circle is the very same circle but oriented in the opposite way.
As a result of his argument, Poncelet arrived at a much more general statement than the one stated above:
Poncelet's General Theorem: Let e be a circle of a non-intersecting pencil and let a1,a2,...,an be (not necessarily different) oriented circles in the interior of e that belong to the same pencil. Starting at an arbitrary point A0 of the circle e, the points A1,A2,...,An are constructed on the same circle, such that the lines A0A1, A1A2, ..., An-1An touch the circles a1,a2,..., an, respectively, in the appropriate direction. It may happen that at the end of the construction, we get back to the starting point, that is, An=A0. The theorem states that in that case, we will always get back to the starting point in the n-th step, whichever point of e we start from. We do not even need to take care to draw the tangents to the circles in a fixed order.
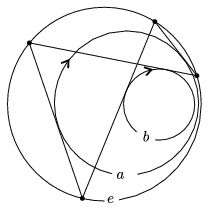
Figure 7
Proof. The composition of the oblique rotations of the circle e with respect to the circles a1,a2,...,an is equivalent to the oblique rotation determined by the directed circle
\(\displaystyle b=a_1\circledast a_2\circledast\dots\circledast a_n \)
of the pencil. This transformation maps the point A0 onto itself, thus the tangent drawn to the directed circle b from A0 cannot intersect the circle e, it must be tangent to e, too. Hence b=e, as all other elements of the pencil lie inside e, and cannot touch it either. The oblique rotation corresponding to e is the identity, therefore if we start at any other point instead of A0, we will get back to that point again. As the group is commutative, the order of the tangents drawn to the given circles does not matter either.
The case of a1=a2=...=an=a gives Poncelet's theorem as stated above. In that case it is not necessary to assign a direction to the circles, as the reversal of the orientation of the circle a (or any one of a1,a2,...,an in the general case) only results in the very same tangents drawn, but in reverse order and in opposite direction.
Elliptic integrals
In 1827, J. Steiner set the following problem in the Journal für die reine und angewandte Mathematik2:
If a pentagon is both cyclic and circumscribed, what is the relationship between the radii of the two circles and the distance between their centres? Solve the same problem for polygons of 6, 7, 8, 9 and 10 sides, too.
Based on Poncelet's theorem, Steiner asked for the algebraic condition for the polygon to close up. Steiner knew the solution in these cases, but he did not set the problem in vain. It raised Jacobi's interest, and Jacobi found a new and extraordinary proof for Poncelet's theorem.
Jacobi was working on elliptic integrals at the time. The problem of elliptic integrals was born out of the investigations of Prince G. Fagnano into the properties of the ellipse and the lemniscate. Fagnano wanted to determine the length of the arc that belongs to a chord of length t drawn from the origin in the lemniscate (x2+y2)2= x2-y2. J. Bernoulli and L. Euler also faced an equivalent question in their studies of elasticity. Neither of them managed to find the function I(t) expressing the length of the lemniscate arc.
What Fagnano achieved was finding the length of the chord that belongs to an arc twice as long as the arc that belongs to t. Euler generalized the method by providing an addition formula to express the length of the chord that belongs to the arc whose length is the sum of the lengths of the arcs that belong to the chords of lengths t1 and t2. He even went beyond that: He described a wide collection of arc length and area problems (integrals, in general) where such an addition formula can be found. These are called elliptic integrals.
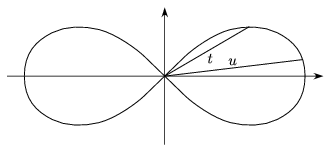
Figure 9. If \(\displaystyle u=\frac{2t\sqrt{1-t^4}}{1+t^4}\) then I(u)= 2I(t)
Jacobi also had remarkable results in this area. In competition with N. H. Abel, they published one article after another in the above mentioned journal. For a change, Jacobi also tried Steiner's problem. He constructed a diagram, drew a few lines in it, expressed their lengths, and to his surprise, he obtained formulae that were strikingly similar to the addition formulae of elliptic integrals. The formulae showed that there was a quantity, an integral that increases by the same amount with each additional side of the Poncelet polygon. In the case of concentric circles, this quantity is the central angle corresponding to the polygon. In that special case, each ``tangent chord'' between the two circles has the same length, and thus the corresponding central angles are also equal. If n times the central angle is 360o or a multiple of it, the polygon will close up in n steps, and otherwise it will not.
Jacobi concluded from the formulae that there is a measure analogous to the central angle in the general case, too. As far as the proof was concerned, it did not matter what the geometrical meaning of the measure was. This is important to emphasize, as however logical the following proof is, and however easy to follow, Jacobi discovered it by an entirely different logic, with an entirely different approach.
Jacobi's proof
The task is to introduce a measure on the circle e of Poncelet's theorem that assigns the same number to the arcs PP' and QQ' if the lines PP' and QQ' both touch the circle a.
Let us try arcs lying close to each other first. It would also be good if the measures of the arcs PQ and P'Q' were equal. Those small arcs have almost the same length as the segments PQ and P'Q'. The segments are, unfortunately, not equal in length, but there is a simple relationship between them. Since the angles subtended at the circumference of circle e are equal, the triangles PQT and Q'P'T are similar. Thus
| (4) | \(\displaystyle \frac{PQ}{PT}=\frac{P'Q}{Q'T}. \) |
The denominators approach the lengths of the tangents drawn to the circle a from the points of the arcs PQ and P'Q'. Therefore, if the opposite arcs PQ and P'Q' are to be assigned the same measure then each of them should be weighted with the reciprocal of the tangent drawn from its points to the circle a.
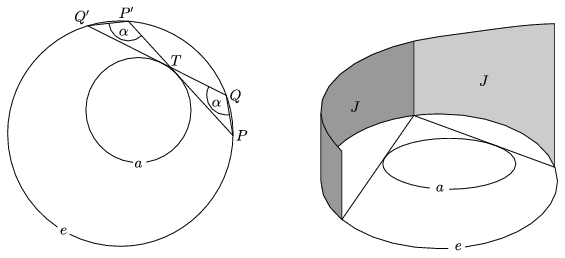
Figure 10
This idea is easy to visualize. Surround the circle e with a surface perpendicular to the plane of the circle, like the lateral surface of a cylinder. The base of the surface is the circle itself, but its height should vary pointwise. At a point P of the circle, set the height of the surface equal to the reciprocal of the length of the tangent drawn from P to the circle a. The area of the surface is the measure required.
We claim that the areas corresponding to the arcs PQ and P'Q' are equal. Each side of equation (4) is an approximation of those areas. The lengths of the segments PQ and P'Q' approach the lengths of the arcs PQ and P'Q', respectively, and the values of \(\displaystyle \frac{1}{PT}\) and \(\displaystyle \frac{1}{Q'T}\) approach the heights of the surface over the arcs. A better approximation of these areas is obtained if the arc PQ and the arc P'Q' opposite are divided into smaller pieces, and each of the smaller pieces is estimated separately with the product of the chord and the corresponding approximate height. If this is always done according to the formula corresponding to the two sides of equation (4), then the areas obtained for the surfaces over the arcs PQ and P'Q' will always be equal. With this technique, the areas over the two arcs can be approached by equal quantities to any desired precision, which is only possible if the two areas themselves are equal.
It follows now that the areas over the arcs PP' and QQ' are also equal. Let the points P and P' move along the circle e so that the chord PP' should remain tangent to the circle a. It follows from the above considerations that the area over the arc PP' will also remain constant. Let the value of that constant area be J, and let the area of the whole surface be I.
Poncelet's polygon will close up in n steps going around e m times if and only if mI=nJ. This condition is independent of the choice of the starting point A0. This completes the proof of Poncelet's theorem. Note that Poncelet's polygon will close up if and only if the quotient \(\displaystyle \frac{J}{I}\) is rational, and the number of steps required for getting back to the starting point is the denominator of this rational number.
The area of the Jacobi surface has the same property as the arc length of the lemniscate. The arc is a transcendent function of the length of chords from a given point, that is, it cannot be expressed with a finite number of elementary functions. But it is possible to generalize Fagnano's duplication formula and set up a formula for multiplying the arc by n, and that will solve the generalized Steiner problem. This work, however, was only completed 25 years later by A. Cayley.
With a little modification, Jacobi's method can also be used for proving the generalized Poncelet theorem. In order to do so, fix a point E on the circle e and define the height of the lateral surface at the point P as the ratio of the tangents drawn to the circle a from the points E and P: \(\displaystyle h(P)=\frac{EE_A}{PP_A}\), which differs only by the constant factor EEA from the above defined height. The motivation for this definition is that it makes the height universal, that is each element of the pencil determines the same surface. This is explained by one of the results obtained above. We have seen that if a, b, e are three elements of a pencil of circles then the ratios of the powers of different points of e with respect to a and b (i.e. the ratios of the tangents, in our case) are equal:
\(\displaystyle \frac{EE_A}{EE_B}=\frac{PP_A}{PP_B}\), that is, \(\displaystyle \frac{EE_A}{PP_A}=\frac{EE_B}{PP_B}\).
If I is the area of the whole surface and J1,J2,..., Jn are the areas over the arcs determined by the tangents drawn to the elements a1,a2,...,an of the pencil then the condition for the polygon to close up is described by the equation
J1+J2+...+Jn=mI.
The validity of this equation is clearly independent of the choice of the starting point.
Problems
1. a) Show that the centres of the members of any pencil of circles are collinear.
b) Let the radius of one circle of a pencil be R, let the radius of another, smaller circle be r, and let d be the distance of their centres. Prove that the value of
\(\displaystyle k=\sqrt{\frac{4Rd}{{(R+d)}^2-r^2}} \)
is independent of the choice of the smaller circle.
c) Show that the pencil is concentric, non-intersecting, tangent and intersecting, respectively if k=0; 0<k<1; k=1; 1<k.
2. Prove that in non-intersecting, tangent and intersecting pencils, respectively there are 2; 1; 0 one point circles, i.e. figures of equation
(x-u)2+ (y-v)2=0.
3. The circumscribed circle of a triangle ABC is e and its incircle is a. Their radii are R and r, respectively, and the distance of their centres is d. The points of tangency on the incircle are X, Y, Z.
a) Prove that the inversion of the circle e with respect to the circle a maps e onto a circle of radius \(\displaystyle R'=\frac{Rr^2}{R^2-d^2}\), and its centre's distance from the centre of a is \(\displaystyle d'=\frac{dr^2}{R^2-d^2}\).
b) Prove that the inversion with respect to the circle a maps the points A, B, C onto the midpoints of the sides of the triangle XYZ.
c) Prove Euler's theorem.
d) Prove Poncelet's theorem for n=3.
4. Find the formula corresponding to Euler's theorem for the circumscribed and escribed circles of the triangle.
5. a) Prove that the equation of the element of the pencil generated by the circles a(x,y)=0, b(x,y)=0 that passes through the point P(\(\displaystyle \xi\),\(\displaystyle \eta\)) is
b(\(\displaystyle \xi\),\(\displaystyle \eta\)) a(x,y)- a(\(\displaystyle \xi\),\(\displaystyle \eta\)) b(x,y)=0.
b) Prove that the equation of the line touching the circle of equation (1) at its point P(\(\displaystyle \xi\),\(\displaystyle \eta\)) is
(\(\displaystyle \xi\)-ua)(x-\(\displaystyle \xi\))+ (\(\displaystyle \eta\)-va)(y-\(\displaystyle \eta\))=0.
c) Prove that the points of tangency on the tangents drawn form a point to the elements of a pencil of circles form a cubic curve.
6. a) Express the equation corresponding to (1) in homogeneous coordinates, and show that the ideal and imaginary points (1,i,0) and (1,-i,0), where i2=-1, lie on the circle.
b) Prove that a nonempty irreducible quadratic curve of real coefficients is a circle if and only if it contains the points (1,i,0) and (1,-i,0).3
Bibliography
[[1]] H. S. M. Coxeter and S. L. Greitzer: Geometry Revisited, Random House (New York, 1967).
[[2]] M. Berger: Géométrie (chapter 16.6); CEDIC/Fernand Nathan (Paris, 1977).
[[3]] A. Shen: Mathematical entertainments, Poncelet Theorem Revisited; The Mathematical Intelligencer, vol. 20, n. 4 (1998), page 31.
[[4]] R. Ayoub: The lemniscate and Fagnano's contribution to elliptic integrals; Archive for history of Exact Sciences, vol. 29, n. 2 (1984), pages 131-149.
[[5]] H. J. M. Bos, C. Kers, F. Oort and D. W. Raven: Poncelet's closure theorem; Expositiones Mathematicae, vol. 5 (1987), pages 289-364.
1 If PR and PQ are considered oriented segments then for interior points the product PR.PQ will be negative, as R and Q lie on opposite sides of R.
2 The Journal for Pure and Applied Mathematics was founded by the Prussian engineer A. L. Crelle, encouraged by Abel and Steiner himself.
3 The introduction of complex numbers into geometry is also a result of Poncelet's considerations. He pointed out that if complex coordinates are allowed then any two quadratic curves have two common points. If those two points are projected to the points (1,i,0) and (1,-i,0) then the two curves are mapped onto two circles. Thus it is enough to prove Poncelet's theorem for two circles.
