Matematikából kitűzött gyakorlatok és feladatok
1997. október

Általános iskolások részére javasolt példák: C. 477., C. 478., Gy. 3150.

A pontversenyben kitűzött C gyakorlatok

C. 477. Egy automatába kétféle korongot dobhatunk be, pirosat vagy zöldet. A gép 1 piros korongért 5 zöldet ad és 1 zöldért 5 pirosat. Ha valaki 1 zöld koronggal kezd el játszani, elérheti-e, hogy ugyanannyi zöld korongja legyen, mint piros, ha elég sokáig játszik?

Angol versenyfeladat

C. 478. Egy számtani sorozat első n elemének összege A, első 2n elemének összege B. Fejezzük ki A és B segítségével az első 3n elem összegét.

Javasolta: Sarinay Dávid, Siófok

C. 479. Egy trapéz párhuzamos oldalai a és c. Mekkora annak a szakasznak a hossza, amely párhuzamos a trapéz megadott oldalaival, és a trapéz területét felezi?

C. 480. Egy tetraéder két lapja egységnyi oldalú szabályos háromszög, két lapja pedig egyenlő szárú derékszögű háromszög. Mekkora a tetraéder térfogata?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. november 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3150. Egy városban minden buszjáratnak 3 megállója van, bármely két megálló között van buszjárat, és bármely két buszjáratnak 1 közös megállója van. Hány buszjárat lehet a városban? (H)

Gy. 3151. Minden pozitív egész n-re jelölje A_n azon pozitív egészek halmazát, amelyek nem relatív prímek n-hez. Milyen n-ekre következik 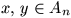-ből, hogy x+y is A_n-ben van?

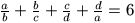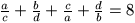Gy. 3152. Az a, b, c, d valós számokra , és teljesül. Mi lehet 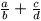értéke?

Gy. 3153. Mennyi a 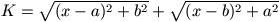kifejezés minimuma, ahol a és b pozitív állandók?

Javasolta: Czirok Levente, Szekszárd

Gy. 3154. Az ABC háromszög oldalait jelöljük a szokásos módon a, b, c-vel. A beírt körhöz az A, B, C csúcsokból húzott érintőszakaszok legyenek rendre x, y és z. Mutassuk meg, hogy ha 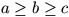, akkor .

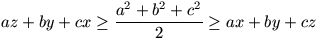Javasolta: Gerő Tamás Miklós, Debrecen

Gy. 3155. Bizonyítsuk be, hogy a háromszög beírható körének középpontján áthaladó egyenes pontosan akkor felezi a háromszög kerületét, amikor a területét is felezi.

Javasolta: Vincze Tímea, Salgótarján

Gy. 3156. Egy háromszögről tudjuk, hogy súlyvonalainak a beírt körbe eső szakaszai egyenlő hosszúak. Következik-e ebből, hogy a háromszög szabályos?

Javasolta: Róka Sándor, Nyíregyháza

Gy. 3157. Egy tetraéderről tudjuk, hogy súlyvonalainak a beírt gömbbe eső szakaszai egyenlő hosszúak. Következik-e ebből, hogy a tetraéder szabályos? (H)

Javasolta: Róka Sándor, Nyíregyháza

A pontversenyben kitűzött feladatok

F. 3190. Van-e olyan 1-nél nagyobb x valós szám, amely nem egész, és teljesül rá a következő egyenlőtlenség?

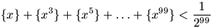
F. 3191. Az n és p pozitív egész számokra teljesül, hogy 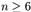, 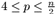. Színezzük ki egy szabályos n-szög p darab csúcsát pirosra, a többit kékre! Bizonyítsuk be, hogy létezik két egybevágó, legalább 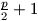csúcsú sokszög, amelyek közül az egyiknek minden csúcsa piros, a másiknak pedig minden csúcsa kék!

F. 3192. Az 5x5-ös sakktáblán lóugrással néhányat léptünk úgy, hogy végül a kiindulási helyre értünk vissza. Lehetséges-e, hogy a sakktábla minden mezőjére pontosan egyszer léptünk?

F. 3193. A torznégyszög csúcsai nincsenek egy síkban. Lehet-e egy torznégyszög mindegyik szöge derékszög?

F. 3194. Az ABC derékszögű háromszög AB átfogójának D egy olyan pontja, amelyre DCA és DCB háromszögekbe írható körök sugara megegyezik. Szerkesszük meg a D pontot.

Javasolta: Mihalovics Sándor, Esztergom

F. 3195. Egy kocka alakú torta teljes felülete (az alja is) csokoládéval van bevonva. A tortát K ember között szeretnénk szétosztani úgy, hogy mindenki ugyanannyi tésztát és ugyanannyi csokoládébevonatot kapjon. Ezt úgy kívánjuk megvalósítani, hogy NxNxN egyforma kis kockára osztjuk a tortát, és mindenkinek ugyanannyi darabot adunk, ügyelve arra is, hogy a kapott részek csokis oldalainak együttes területe megegyezzen. Megtehető-e ez tetszőleges K-ra? Legalább hány részre kell felvágni a tortát, ha K=1997?

Javasolta: Blázsik Zoltán, Szeged

A pontversenyben kitűzött nehezebb feladatok

N. 148. Adott a síkon 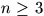páronként különböző pont. Bizonyítsuk be, hogy kiválasztható közülük három különböző: A, B és C, amelyekre .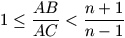

Javasolta: Pap Gyula, Debrecen

N. 149. Definiáljuk az (a_n) sorozatot a következőképpen: a₀=a₁=1, (n+1)a_n+1=(2n+1)a_n+3na_n-1. Mutassuk meg, hogy a sorozat egész számokból áll.

N. 150. Adott a síkon egy parabola, és rajta kívül a P és Q pontok úgy, hogy a PQ egyenes átmegy a parabola fókuszpontján. Igazoljuk, hogy ha P-ből és Q-ból két-két érintőt húzunk a parabolához, a keletkező négy metszéspont egy körön lesz.

N. 151. Az a₂, a₃, ... pozitív valós számokból álló sorozat, és 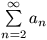konvergens. Bizonyítsuk be, hogy ekkor a 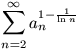sor is konvergens.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. november 15.