Matematikából kitűzött gyakorlatok és feladatok
1997. december

Általános iskolások részére javasolt példák: C. 486., Gy. 3168., Gy. 3173.

A pontversenyben kitűzött C gyakorlatok

C. 485. Egy 100 sorból és 100 oszlopból álló táblázat első oszlopában csupa 1-es található, k-adik sorában pedig olyan számtani sorozat, amelynek differenciája k. A táblázat bal alsó sarkától jobb felső sarkáig húzódó átlója mentén elhelyezkedő számok közül melyik a legnagyobb?

C. 486. Hányféleképpen fizethető ki 25 forint 1, 2, 5, 10 és 20 forintos érmékből?

C. 487. Bizonyítsuk be, hogy ha 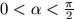, akkor .

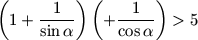C. 488. Egy egyenes csonkakúp palástját oldalmagasságának feléig kékre festettük, azon felül pirosra. A kék színű felület kétszer akkora, mint a piros. Hányszorosa az alapkör sugara a fedőkör sugarának?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. január 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3166. Melyik a nagyobb: 1997¹⁹⁹⁹ vagy 1999¹⁹⁹⁷?

Javasolta: Árokszállási Tibor, Paks

Gy. 3167. Bizonyítsuk be, hogy az a, b pozitív egészeknek pontosan akkor azonos a paritása, ha vannak olyan c, d pozitív egészek, amelyekre a²+b²+c²+1=d².

Gy. 3168. Adjuk meg egy 15 elemű halmaznak 15 darab 7 elemű részhalmazát úgy, hogy bármely két különböző részhalmaz metszete 3 elemű legyen! (H)

Gy. 3169. Melyek azok az egész oldalhosszúságú háromszögek, amelyek egyik szöge a másiknak kétszerese?

Javasolta: Mihalovics Sándor, Esztergom

Gy. 3170. Az ABC háromszög C-nél levő szöge derékszög. A B csúcsból induló szögfelező az AC oldalt a P, a háromszög köré írt kört a Q pontban metszi. Mekkorák a háromszög szögei, ha BP=2PQ?

Javasolta: Czirok Levente, Szekszárd

Gy. 3171. Egy háromszög egyik oldala egységnyi, és a másik két oldal ennek egész számú többszöröse. %Egy háromszög oldalai egész számok, az egyik oldal egységnyi. Lehet-e a háromszögbe írható kör sugara racionális? (H)

Javasolta: Mihalovics Sándor, Esztergom

Gy. 3172. Egy függőleges tengelyű, felül nyitott egyenes körhenger alakú, vízzel színültig tele edényt 30^o-kal megdöntünk. Mennyi víz folyik ki az edényből, ha a henger sugara 10 cm, magassága 25 cm? Szerkesszük meg azt a szöget, amellyel az edényt megdöntve, az eredetileg benne lévő víz fele folyik ki.

Gy. 3173. A tér egy P pontján át három egyenes halad. Szerkesszünk P-n át olyan síkot, amely mindegyik egyenessel ugyanakkora szöget zár be.

A pontversenyben kitűzött feladatok

F. 3202. Legyen n prímtényezős felbontása 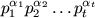. Jelölje r₁, r₂, ..., r_m azokat az n-nél kisebb pozitív egész számokat, amelyek n-hez relatív prímek. Mutassuk meg, hogy .

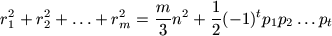F. 3203. Bizonyítsuk be, hogy egy 15 elemű halmaznak létezik 15 darab olyan 6 elemű részhalmaza, amelyek közül bármely két különböző metszetének elemszáma 1 vagy 3.

Javasolta: Dr. Spissich László, Pápa

F. 3204. Két játékos a következő játékot játssza: 923^k darab kavicsból felváltva elvesznek 9 vagy 2 vagy 3 kavicsot. Az veszít, aki már nem tud így elvenni. Van-e valamelyik játékosnak nyerő stratégiája?

Javasolta: Vörös Zoltán, Budapest

F. 3205. Igazoljuk, hogy egy tetszőleges háromszögben: 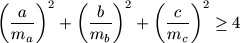, ahol a, b, c a háromszög oldalainak, m_a, m_b, m_c a megfelelő magasságainak hosszát jelöli.

Javasolta: Árokszállási Eszter, Paks

F. 3206. Adott a k₁ kör és a rajta kívül levő H₁, H₂ és P pontok. Szerkesszünk a P-n át olyan k₂ kört, amelyhez a H_i pontokból húzott érintők hosszai egyenlők a H_i-ből a k₁ körhöz húzott érintők hosszaival (i=1,2).

F. 3207. Egy 2 egységnyi élű szabályos tetraéder két-két csúcsa egy egyenes körhenger alap-, illetve fedőlapjának kerületén van. Mekkora a körhenger térfogata?

A pontversenyben kitűzött nehezebb feladatok

N. 155. Bizonyítsuk be, hogy ha egy pozitív egészekből álló végtelen sorozatban mindegyik elemnek ugyanannyi osztója van, akkor létezik olyan végtelen részsorozata, amelyben bármelyik két elem legnagyobb közös osztója ugyanaz.

N. 156. Bizonyítsuk be, hogy ha az a₁,a₂,... és b₁,b₂,... egészekből álló sorozatokra a₁=b₁=0, és 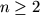esetén a_n=nb_n+a₁b_n-1+a₂b_n-2+a₃b_n-3+...+a_n-1b₁, akkor bármely p prímszámra a_p osztható p-vel.

Javasolta: Pap Gyula, Debrecen

N. 157. Egy nxn-es táblázat valós számokkal van kitöltve úgy, hogy minden sorban és minden oszlopban az elemek monoton fogynak. Egy a számról el szeretnénk dönteni, hogy szerepel-e a táblázatban. Ehhez a-t a táblázat tetszőleges elemével összehasonlíthatjuk. Hány összehasonlítással oldható meg biztosan a feladat?

Javasolta: Csirmaz László, Budapest

N. 158. Adott a térnek 9 olyan konvex részhalmaza, amelyek közül bármely 8 metszete tartalmaz rácspontot. Igazoljuk, hogy létezik olyan rácspont, amely mindegyik halmaznak eleme.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. január 15.