New exercises and problems in Mathematics
March 1998
New exercises for practice in March 1998
C. 497. Is there any positive integer n such that 1.2.3.....(n-1).n, that is, n!, ends with exactly 100 zeros?
C. 498. Solve inequation x3+1>x2+x.
C. 499. There is given a circle of unit radius in the plane. A wreath of n congruent circles is formed around the given circle such that each circle in the wreath touches its two neighbours and also the given circle. Determine, in terms of n, the common radius of the circles. Calculate these radii, up to four digits precision after the decimal point, for the first four possible values of n.
C. 500. Is it possible to slip two fine arts albums, each 22 cm wide, and a 25 cm wide cookbook into 28 cm wide plastic bag? Assume that each book has a thickness of 1.5 cm.
New exercieses in March 1998
Gy. 3190. We define a number 44...48...89 with the following procedure. First, we insert the number 48 between the two digits of 49. Next, 48 is inserted between the digits 4 and 8 of the resulting number. Finally, we repeat this second step a few times. Is it true that every number obtained this way is a perfect square?
Gy. 3191. Is it true that every integer has at least as many positive divisors of the form 4k+1 as that of the form 4k-1?
Gy. 3192. Find all pairs of positive integers A,B with the following property: if the decimal representation of A is placed in front of that of B, then the resulting number is a perfect square, equal to twice the product of A and B.
Gy. 3193. A basketful of peanuts is distributed into n piles. We gather the piles and rearrange them into n+k new piles (k>0). Prove that at least k+1 peanuts are transferred to smaller piles than the respective original piles that contained them. (H)
Gy. 3194. In a triangle, two of the altitudes are at least as long as the corresponding sides of the triangle. Find the angles of the triangle.
Gy. 3195. In a right triangle, parallel lines to each side are drawn through the incentre of the triangle. These lines divide each side of the triangle into three parts. Prove that the length of the middle part of the hypotenuse equals the sum of the lengths of the middle parts arising on the legs of the triangle.
Gy. 3196. There are given rays e0, e1, ..., e6, each starting at the same point A of the plane. Each ray forms an angle of 30o with the one that precedes it in the given order. Let B0 denote the point on ray e0 such that A and B0 are a unit distance apart. Let B1 denote the orthogonal projection of B0 to e1. Similarly, denote by B2 the orthogonal projection of B1 to e2, and so on. Calculate the length of the polygonal path B0B1...B6 and the area of polygon B0B1...B6.
Gy. 3197. Four balls, each of radius r, are placed on a horizontal plane such that each of them touches two others and their centres form a square. A fifth ball of the same radius is placed on the top of these balls, touching all of them. Calculate the distance of the topmost point of the fifth ball from the given plane. (H)
New problems in March 1998
F. 3220. A rectangular field is divided into 100 congruent rectangular plots with the help of lines parallel to the edges of the field. Neighbouring plots share a common edge. Initially, 9 plots of the field are overgrown with weeds. The weeds overgrow any plot whose (at least) two neighbours are already overgown. Is it possible that the whole field becomes overgrown sooner or later?
F. 3221. The numbers 1,2,...,n are assigned, in some order, to the vertices of a regular n-gon A1A2...An.
- a) Determine the maximum possible value of the sum of the absolute values
of the differences between numbers assigned to consecutive vertices.
- b) Find the number of arrangements for which the above sum is maximum.
F. 3222. Given that n is a prime, prove that there is no positive integer x that satisfies equality (1n+2n+...+xn)+(1n+2n+...+(n-1)n)=1n+2n+...+(2n-1)n.
F. 3223. A polygon has exactly n axes of symmetry. How many sides may the polygon have?
F. 3224. In a certain convex polytope, every face has a central symmetry. Prove that at least six of the faces are parallelograms.
F. 3225. Find a set of points in 3-space which intersects every plane in at least one but not more than five points.
New advanced problems in March 1998
N. 167. There are given three unit discs in the plane. Let
t1 and t2 denote the areas of the two
regions in the plane which the discs cover exactly once resp. exactly twice.
Prove that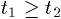 
.
N. 168. Prove that equality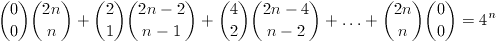 
holds for every positive integer n.
N. 169. Let an denote the number of possible
results of a contest with n participants, where ties may occur.
For example, a2=3 and a3=13.
Prove inequality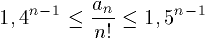 
.
N. 170. Given that 15a+6b+4c+8d=0, prove that the equation ax3+bx2+cx+d=0 has a positive root.