New exercises and problems in Mathematics
May 1998

New exercises for practice in May 1998

C. 505.  Let us call a calendar week even or odd according to the parity of the sum of the numbers of the days in the seven dates making up that week. How many even weeks can there be among any 52 consecutive weeks that counted from the first Monday in January?

C. 506. Find all pairs of integers m and n for which the equation

(2m-3)(n-1)x²+(2m-3)(n-1)(m-n-4)x-2(2m-3)(n-1)(m-n-2)-1=0 has integer solutions.

C. 507. Find the locus of the vertex of the parabola y=x²+tx+1 where t varies through the real numbers.

C. 508. Our train travels on a straight railway track at a constant velocity of 26 m/s. Looking out of the window, we notice a cylindrical grain silo. As we approach the silo for 5 seconds, our distance from the silo is reduced by 100 m, while the silo seems to turn through an angle of 5^o. How much longer do we continue to get closer to the silo?

New exercieses in May 1998

Gy. 3206. Given 2n distinct points on a line; points A₁, A₂, ..., A_n are red and points B₁, B₂, ..., B_n are blue. Consider all segments determined by the given points, and draw circles with these segments as diameters. A circle is then coloured red if the endpoints of its diameter are of the same colour. The other circles are coloured blue. Prove that the total length of the perimeters of the blue circles is at least as large as that of the red circles.

Gy. 3207. A certain number can be written in the form 3a²+32b², where a and b are natural numbers. Multiply the number by 97. Prove that the new number can be expressed in that form too.

Gy. 3208. Solve the equation x(x-y)+y(y-z)+z(z-x)=1 in the set of integers.

Gy. 3209. Which polynomials p(x) satisfy the following equality: (x-16)p(2x)=16(x-1)p(x)?

Gy. 3210. An inscribed trapezium is divided by its two diagonals into four triangles. Prove that each triangle has a circumcentre lying on one of the perpendicular lines dropped from the intersection point of the diagonals onto the sides of the trapezium.

Gy. 3211. There are given infinitely many rectangles in a Cartesian coordinate system such that each rectangle has an edge lying on the x axis and another one lying on the y axis. Moreover, the vertices of the rectangles opposite to the origin have integer coordinates. Prove that there are two rectangles such that one is contained in the other.

Gy. 3212. There are given 6 points in the plane, no three collinear. A few pairs of the given points are connected with line segments. At least how many segments must be drawn so that there should always be a triangle formed with its vertices being three of the given points?

Gy. 3213. Given a convex pentagon and a point P on its boundary, construct a line passing through P that halves the area of the pentagon.

New problems in May 1998

F. 3232. Find all positive integer solutions to the equation .

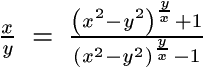F. 3233. Let b(n) denote the minimum value of expression 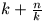, where k is a positive integer. Prove that for any natural number n, .

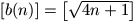F. 3234. In an all-aginst-all tournament, three teams are said to `beat around' each other if each of them wins exactly once when only games among those three teams are considered. At most how many beat-arounds may happen in a tournament with 23 participating teams?

F. 3235. Two 1998-gons are drawn in the plane such that the midpoints of their sides coincide. Does it imply that the polygons have equal areas?

F. 3236. Given a convex polygon K and a point P inside the polygon, prove that there exists a direction such that of all lines parallel to it, the one passing through P has the longest segment in K.

F. 3237. The diagonals of a certain four-sided prism pass through a common point. Prove that the prism is a parallelopiped.

New advanced problems in May 1998

N. 175. There are n natural numbers written along a circle. We write the absolute value of their difference between every two consecutive numbers, and then erase the original numbers. We may repeat this procedure a finite number of times. Determine those values of n for which all numbers along the circle will be eventually zero, regardless of the particular choice of the original numbers.

N. 176. A piece is moving on an nxn board, its moves are restricted to one horizontal or one vertical step at a time. It starts at the upper left corner of the board and visits each field of the board exactly once. Let t_n denote the number of different possible routes of the piece. Prove that 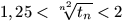, if n is large enough. Is it possible to improve upon the upper bound?

N. 177. An automatic card shuffler is designed to shuffle, for any positive integer n, a deck of 2n cards according to the following rule:
(1,2,3,...,2n)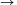(2n,1,2n-1,...,n+1,n). We start with 1998 different cards. We complete the deck by adding 2n-1998 new cards to it, and feed the deck of 2n cards, in some order, to the machine. Is it possible to choose n and the order of the cards in such a way that every permutation of the original 1998 cards should occur in some finite number of shuffles?

N. 178. Let n denote any positive integer. Prove that there exists a set of n real numbers in which any three distinct elements x, y, z satisfy eithe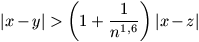r or .
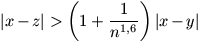