Matematikából kitűzött gyakorlatok és feladatok
1998. május

Általános iskolások részére javasolt példák: C. 505., Gy. 3206., Gy. 3207., Gy. 3210.

A pontversenyben kitűzött C gyakorlatok

C. 505. Egy naptári hetet nevezzünk párosnak vagy páratlannak aszerint, hogy a benne szereplő napok hónapon belüli sorszámainak összege páros, illetve páratlan. Az első januári hétfőtől kezdődő 52 egymás utáni hét közül hány lehet páros?

C. 506. Határozzuk meg mindazokat az m és n egész számokat, amelyek esetén a következő egyenlet gyökei ugyancsak egész számok:

(2m-3)(n-1)x²+(2m-3)(n-1)(m-n-4)x-2(2m-3)(n-1)(m-n-2)-1=0.

C. 507. Mi az y=x²+tx+1 egyenletű parabolák tengelypontjainak (csúcspontjainak) mértani helye? (t valós paraméter.)

C. 508. Egyenes pályán 26 m/s sebességgel haladó vonat ablakából kitekintve a távolban egy henger alakú gabonatárolót látunk. 5 másodperc alatt a tárolóhoz állandóan közeledve távolságunk a tárolótól 100 m-rel csökken, miközben a tároló látszólag 5^o-kal elfordul. Mennyi ideig közeledünk még a tárolóhoz?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. júniuus 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3206. Egy egyenesen adott 2n különböző pont. Közülük az A₁, A₂, ..., A_n piros színű és a B₁, B₂, ..., B_n kék színű. E pontok által meghatározott szakaszok mint átmérők fölé köröket rajzolunk. A körvonalakat pirossal vagy kékkel színezzük aszerint, hogy az átmérőjük végpontjai azonos vagy különböző színűek. Mutassuk meg, hogy a kék körvonalak összhossza legalább akkora, mint a pirosaké.

Gy. 3207. Bizonyítsuk be, hogy ha egy szám felírható 3a²+32b² alakban, ahol a és b természetes számok, akkor a 97-szerese is felírható ilyen alakban.

Litván versenyfeladat

Gy. 3208. Oldjuk meg az egész számok halmazán az x(x-y)+y(y-z)+z(z-x)=1 egyenletet.

Gy. 3209. Mely p(x) polinomra teljesül az (x-16)p(2x)=16(x-1)p(x) egyenlőség? (H)

Ír versenyfeladat

Gy. 3210. A húrtrapézt két átlója négy háromszögre bontja. Bizonyítsuk be, hogy bármelyik háromszög köré írt kör középpontja rajta van az átlók metszéspontjából a trapéz oldalaira állított merőleges egyenesek valamelyikén.

Gy. 3211. Végtelen sok téglalapot úgy helyeztünk el egy derékszögű koordináta-rendszerben, hogy mindegyiknek egyik oldala az x, egy másik oldala az y tengelyre illeszkedik. A téglalapok origóval szemközti csúcsának koordinátái pozitív egész számok. Bizonyítsuk be, hogy van a téglalapok között két olyan, amelyek közül az egyik tartalmazza a másikat.

Gy. 3212. A sík 6 adott pontja közül semelyik három nincs egy egyenesen. A pontpárokat összekötő szakaszok közül hányat kell meghúzni ahhoz, hogy biztosan legyen olyan háromszög, amelynek csúcsai az adott pontok közül valók?

Gy. 3213. Adott egy konvex ötszög kerületén egy P pont. Szerkesszünk olyan P-n átmenő egyenest, amely felezi az ötszög területét. (H)

A pontversenyben kitűzött feladatok

F. 3232. Keressük meg az 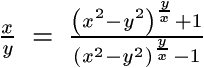egyenlet pozitív egész megoldásait.

Bencze Mihály, Brassó

F. 3233. Jelölje b(n) a 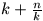kifejezés minimumát, ahol k a pozitív egészeken fut végig. Bizonyítsuk be, hogy ha n természetes szám, akkor .

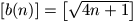F. 3234. Egy körmérkőzéses bajnokságon 23 csapat vett részt. Minden csapat az összes többivel pontosan egyszer játszott. Azt mondjuk, hogy 3 csapat körbeverte egymást, ha csak az egymás közötti játékot nézve, mindegyikük pontosan egyszer nyert. Legfeljebb hány körbeverés történhetett a bajnokság alatt?

Amerikai vizsgafeladat

F. 3235. Két 1998-szög oldalfelező pontjai egybeesnek. Igaz-e, hogy egyenlő a területük?

F. 3236. Adott egy K konvex sokszög és a belsejében a P pont. Mutassuk meg, hogy van olyan irány, hogy az azzal párhuzamos egyenesek közül a P-n átmenőnek esik a leghosszabb darabja K belsejébe.

F. 3237. Mutassuk meg, hogy ha egy négyszög alapú hasáb testátlói egy ponton mennek át, akkor a hasáb paralelepipedon.

A pontversenyben kitűzött nehezebb feladatok

N. 175. Egy kör kerületére n darab természetes számot írtunk. Egy lépés során minden szomszédos számpár közé beírjuk a különbségük abszolút értékét, majd az eredeti számokat kitöröljük. Mely n-ekre biztos az, hogy véges sok lépés után már csupa nulla marad a körön?

N. 176. Egy nxn-es táblázaton egy bábu fel, le, balra, jobbra tud egyet-egyet lépni. Elindul a bal felső sarokból, és bejár minden mezőt pontosan egyszer. Ezt a bábu t_n-féle útvonalon tudja megtenni. Bizonyítsuk be, hogy elég nagy n-re .
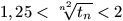Adható-e jobb felső becslés?

N. 177. Egy kártyakeverő gép a következő keverési lépést bármely n-re el tudja végezni:
(1,2,3,...,2n)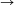(2n,1,2n-1,...,n+1,n).
Van 1998 db különböző lapunk. Ezeket kiegészítjük 2n-1998 új lap hozzávételével, majd ezt a 2n lapból álló csomagot valamilyen sorrendbe rendezve a gépbe helyezzük. Elérhető-e (az n és a kezdeti sorrend alkalmas megválasztásával), hogy az 1998 lap egymáshoz képest minden lehetséges sorrendben előforduljon véges sok keverési lépés után?

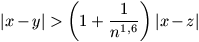N. 178. Bizonyítsuk be, hogy tetszőleges pozitív egész n-re létezik olyan valós számokból álló, n elemű halmaz, amelynek bármely három különböző x, y és z elemére vagy , vagy 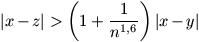teljesül.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. június 15.