Fizikából kitűzött gyakorlatok és feladatok 1998. október

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

m. 200. A TV készülék távirányítója láthatatlan, infravörös fényt bocsát ki. Vizsgáljuk meg, hogy mennyire engedik át és mennyire verik vissza papírlapok ezt a fényt! (6 pont)

Közli: Horányi Gábor, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

FGy. 3184. A hóval borított sportpályát egy tolólapátos erőgéppel takarítják. A gép állandó sebességgel halad, és eközben az előtte levő havat a pálya szemközti oldalára tolja. A pálya hossza kétszerese a szélességének. Hogyan mozogjon a gép a pályán, hogy a végzett munka kevesebb legyen: keresztben, vagy hosszában? Mennyi a munkák aránya? (3 pont) (Á)

Közli: Farkas László, Keszthely

FGy. 3185. Egy tanuló sorba kapcsolt négy egyforma 1,5 V-os elemet és egy 6 V-os akkumulátort. Az így kapott ,,telepre'' rákötött egy 6 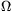-os ellenállást. Ezen az ellenálláson is 6 V lett a feszültség. Ezek után 1, 2, 3 majd 4 elemet vett ki az áramkörből, és meglepődve tapasztalta, hogy az ellenálláson a feszültség mindegyik esetben 6 V maradt. Kis gondolkodás után rájött, hogy nincs ebben semmi ördöngösség. Miért? (4 pont) (Á)

Közli: Radnai Gyula, Budapest

FGy. 3186. Egyatomos ideális gáz állandó nyomáson tágul, miközben energiája 3 kJ-lal megnő. Mennyi munkát végez? Mennyi hőt vesz fel? (3 pont)

Közli: Ujhelyi László, Budapest

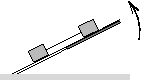FGy. 3187. Vízszintes helyzetű deszkán két, egyenként 2 kg tömegű test nyugszik. A testeket elhanyagolható tömegű, feszes fonál köti össze. A deszka egyik végét lassan emelni kezdjük. Az alul levő testnél a súrlódási együttható 0,2, a felül levőnél 0,5. Mekkora erő feszíti a fonalat, amikor a testek már csúsznak? (4 pont)

Közli: Kotek László, Pécs

FGy. 3188. A kis herceg hátizsákkal érkezik egy kisbolygóra. A következő három megfigyelésből ki tudja számítani a bolygó sűrűségét:

a) A Földön hátizsákjával együtt negyed olyan magasra tudott ugrani, mint anélkül.

b) A bolygón hátizsákjával K-szor olyan magasra tud ugrani, mint amennyit közben a bolygó elmozdul.

c) A bolygó körüli körpályára állítva a hátizsákját, azt t idő múlva kapja el.

Közli: Simon Péter, Pécs

FGy. 3189. Egy diák A Hale-Bopp üstökösről 4 perces expozíciós idővel készített felvételeket. A Föld forgásának következtében a képen a csillagok ,,csíkot húztak'' maguk után. Becsüljük meg a következő adatokból a Föld forgási szögsebességét: A fényképezőgép objektívjének fókusztávolsága 300 mm, a negatívokról 4-szeres nagyítást kért, ezen az egyik csillag nyomát 23 mm-nek mérte. (4 pont)

Közli: Friedl Zita, Sopron, Széchenyi I. Gimn.

FF. 3190. Hol kell felfüggeszteni egy homogén tömegeloszlású rudat, hogy az így kapott fizikai inga lengésideje a lehető legkisebb legyen? (5 pont)

Közli: Pál András, Budapest

FF. 3191. Állandó 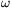szögsebességgel forgatunk egy vékony fémrudat a középpontján átmenő és a rúdra merőleges forgástengely körül, a forgástengellyel párhuzamos homogén mágneses mezőben. Milyen töltéseloszlás alakul ki a rúd belsejében? (5 pont)

Közli: Rácz György, Mezőkövesd

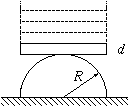FF. 3192. Helyezzünk el egy dominót egy, a lapján fekvő félhenger tetejére az ábrán látható módon. Ha a dominót kis szöggel kitérítjük, majd elengedjük, periodikus, billegő mozgást végez a félhenger tetején. Hány dominót helyezhetünk egymás tetejére úgy, hogy ilyen billegések létrejöhessenek? Mekkora lehet egy 2R hosszú dominó legnagyobb szögkitérése, hogy még éppen ne csússzon le a félhengerről, ha közöttük a tapadó súrlódási együttható 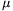=0,1? (A dominó vastagsága d=5 mm, a henger sugara R=3 cm.) (6 pont)

Közli: Holics László, Budapest

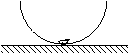FF. 3193. M tömegű, R sugarú, vékony félgömbhéj aljáról egy M tömegű bogár mászik fel a félgömbhéj belsejében, egészen annak felső pereméig.

a) Mekkora munkát végez?

b) Legalább mekkora a tapadási súrlódási tényező a bogár és a félgömbhéj között, ha a bogár fel tud mászni?

c) Van-e szerepe a vízszintes asztal és a félgömbhéj közötti súrlódásnak?

Közli: Varga István, Békéscsaba

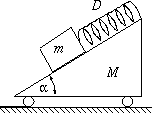FN. 3194. Mekkora frekvenciával rezeg az ábrán látható M tömegű test, ha a súrlódás mindenütt elhanyagolható? (6 pont)

Közli: Balogh Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. november 11.