New exercises and problems in Mathematics
November 1998
 |
New exercises for practice in November 1998 |
C. 518. Solve the following system of equations:
x2+yz=0,
v2+yz=0,
(x+v)y=2,
(x+v)z=-2.
C. 519. Given a circle of unit radius, construct a square such that two consecutive vertices of the square lie on the circle, and the side connecting the other two vertices is tangent to the circle. Determine the length of the side of the square.
Fried Katalin (Budapest)
C. 520. In three dimensional Euclidean space, consider the sphere of radius 3 centered at the origin. Find the number of lattice points (points with integer coordinates) that lie on the sphere.
 |
New exercieses in November 1998 |
Gy. 3230. Is there any sequence a1, a2, ... of natural numbers such that, for every natural number k, the sequence a1+k, a2+k, a3+k, ... contains only a finite number of primes?
Gy. 3231. Do there exist integer numbers a, b, c such that each of the equations
ax2+bx+c=0 and (a+1)x2+(b+1)x+(c+1)=0
has two real solutions?
Russian contest problem
Gy. 3232. How many hundred-digit natural numbers can be formed such that only even digits are used and any two consecutive digits differ by 2?
Gy. 3233. Given 100 different positive integers, prove that some 98 of them can be selected such that their sum is not divisible by the sum of the two remaining numbers.
Gy. 3234. Partition a rectangle into 9 rectangular pieces such that no two pieces can be arranged to form an other rectangle.
Gy. 3235. There are given in the plane two segments AB and CD. Construct a point P such that triangles APB and CPD are similar, having equal angles at vertex P.
Gy. 3236. In an acute-angled triangle ABC, Ta denotes the foot of the altitude dropped from vertex A. Points Tb and Tc are defined in a similar way. Prove that the sum TaC+TbA+TcB is at least as large as the perimeter of triangle TaTbTc.
Árokszállási Tibor (Paks)
Gy. 3237. Is it possible to intersect a cube by a plane in a) a regular pentagon b) a regular hexagon?
|
New problems in November 1998 |
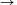R that satisfy
f(x.y)=x.f(x)+y.f(y).
F. 3251. At a ping-pong contest, each player played one game with each of the other players. A player A won a prize if, for any other player B, either A won against B, or A beat someone who won against B. Prove that if exactly one contestant won a prize, then he won against each of the other players.
Chinese contest problem
F. 3252. How many different ways are there to arrange the numbers 1,2,...,n in a single row such that every number, except the number which occurs first, is preceded by at least one of its original neighbours?
F. 3253. Given a circle k and a point P that lies on the circle, construct the line tangent to k at P, using a straight-edge alone.
F. 3254. A transformation of the
plane maps the point P(x;y)
onto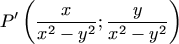 
if 
,
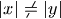and onto itself if |x|=|y|. Describe the images of all straight
lines under the above transformation.
F. 3255. There are given a sphere of unit radius and four pairwise nonintersecting balls whose centres lie on the sphere. The sum of the radii of the balls equals 2. Prove that at least one quarter of the surface area of the sphere is covered by the balls.
 |
New advanced problems in November 1998 |
N. 187. Four distinct points A, B, C and M are given on a sphere, none of which is opposite to any other. Prove that if the great circles AM and BM are orthogonal to great circles BC and AC, respectively, then also the great circle CM is orthogonal to great circle AB.
N. 188. A tree graph is said to be of type pn if it has n levels in addition to its root, and at every vertex, with the exception of the vertices of the topmost level, branches out into p directions.
a) The leaves (topmost vertices) of a graph of type 4n are coloured by 3k colours. Prove that the graph has a subgraph of type 2n whose leaves bear at most k different colours.
b) Show, for each positive integer k, a graph of type 4n whose leaves can be coloured by 3k+1 colours such that any of its subgraphs of type 2n has k+1 leaves which bear different colours.
Keleti Tamás (London)
N. 189. Prove that arbitrary positive integers a1, ..., an satisfy the following inequality:
.
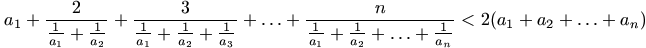N. 190. A polynomial p has degree at most
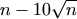. Prove that
.
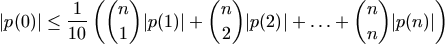