Fizikából kitűzött gyakorlatok és feladatok 1999. január

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást). Az FGy. 3214. és FF. 3221. feladatok közül csak az egyik választható.

Mérési feladat

m. 203. Mérjük meg minél pontosabban a mokkacukor, a kristálycukor, a porcukor és a szaloncukor sűrűségét! Hogyan befolyásolja a sűrűséget a nedvességtartalom? (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

FGy. 3214. Egy falióra nagymutatójának hossza 24 cm. Milyen hosszú a kismutató, ha a hegye 18-szor lassabban mozog, mint a nagymutatóé? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

FGy. 3215. Mekkora energiabefektetéssel szakítható ki egy CO₂ molekula a szárazjégből? (A szükséges adatok a Függvénytáblázatból vehetők.) (4 pont)

Közli: Szűcs Zsuzsa, Budapest

FGy. 3216. Lánctalpas traktor vízszintes úton halad 36 km/h sebességgel.

a) Határozzuk meg az egyik, 600 kg tömegű lánctalp mozgási energiáját!

b) Mennyi a lánctalp mozgási energiája a traktorvezető szerint? (4 pont)

Közli:Kotek László, Pécs

FGy. 3217.  Kirándulók a reggeli induláskor a víz forráspontját 99 ^oC-nak, majd hegyes-völgyes terepen haladó út végén, napnyugtakor 97 ^oC-nak mérték. A Függvénytáblázat adatainak felhasználásával becsüljük meg a két hely közötti szintkülönbséget! A hőmérséklet mindkét helyen mindkét alkalommal 15 ^oC volt, és a légnyomás aznap nem változott! (4 pont)

Közli: Szegedi Ervin, Debrecen

FF. 3218.  Egy kettőscsillag keringési ideje 2 év, a két csillag távolsága 300 millió km, és az egyik csillag tömege a Nap tömegével egyenlő. Mekkora a másik csillag tömege? (4 pont)

Közli: Szalóki Dezső, Budapest

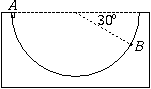FF. 3219.  Egy vízszintes tengelyű, félhenger alakú, rögzített vályú felső pereménél (az ábrán az A pontban) kezdősebesség nélkül elengedünk egy kicsiny, lapos testet, amely leszánkázik a lejtőn.

a) Vajon elcsúszik-e a test a B pontig, ha a test és a vályú között a súrlódási együttható 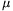₁=0,5?

b) Eljut-e a test a B pontig, ha a súrlódási együttható 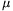₂=0,268? (5 pont)

Közli: Károlyházy Frigyes, Budapest

Mikola-verseny, Sopron

FF. 3220.  Valamely ellipszis alakú pályán egyenletes 5 m/s sebességgel mozgó, 0,5 kg tömegű pontszerű testre a nagytengely végpontjaiban 10 N, a kistengely végpontjaiban 1,25 N erő hat. Mekkorák az ellipszis tengelyei? (5 pont)

Közli: Holics László, Budapest

FF. 3221.  Éjfél után leghamarabb mikor változik az FGy. 3214. gyakorlatban szereplő falióra mutatóinak végpontjai közötti távolság a leggyorsabban, és mikor a leglassabban? (5 pont)

Közli: Radnai Gyula, Budapest

FF. 3222.  Cézium fotokatódra 0,5 W/cm² erősségű, 0,4 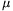m hullámhosszú fény esik a felületre merőlegesen. Az elektronok kilépési munkája 2 eV. Ha az elektronok is a felületre merőlegesen lépnek ki a céziumból, mekkora nyomást fejtenek ki rá? Hányszorosa ez a fotokatódra eső fénynyomásnak? (Tételezzük fel, hogy a beeső fotonok fele nyelődik el, a többi merőlegesen verődik vissza, és az elnyelt fotonok 10 százaléka vált ki fotoelektronokat.) (5 pont)

Közli: Bíró Tibor, Marosvásárhely

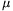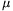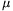FN. 3223.  Két ujjunkkal a két végén alátámasztva, vízszintes helyzetben tartunk egy m tömegű, l hosszúságú, homogén rudat. Ha ujjainkat lassan egymás felé közelítjük, végül a rúd alatt középen fognak találkozni, miközben hol az egyik, hogy a másik ujjunkon csúszik meg a rúd. Mennyi munkát végzünk a folyamat során, ha a tapadó súrlódási együttható _t, a csúszási súrlódásé pedig _cs (_t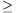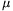cs)? (6 pontÖ

Közli: Balogh Péter, Budapest

Helyesbítés

Az 1998. évi novemberi számban az FF. 3200. számú feladat hibás, ellentmondó adatokkal jelent meg. A feladat helyesen:

FF. 3200.  Egy fizikus által írt levélből idézünk: ,,Két egyforma, m=0,4 kg tömegű korongot könnyű, nyújtatlan, D=10 N/m erősségű húzó-nyomó rugóval kötöttem össze. A korongokat vízszintes talajra tettem, majd az egyik korongot v₀=2 m/s kezdősebességgel meglöktem a korongokat összekötő egyenes mentén úgy, hogy a másiktól távolodni kezdjen. Méréseim szerint a meglökött korong kezdeti lassulása 3 m/s² volt, a korábbi megfigyeléseimből azt is tudtam, hogy a tapadási súrlódás együtthatója éppen akkora, mint a csúszási súrlódásé. Megfigyeltem, hogy a rendszer mozgása négy szakaszból állt. Megmértem a mozgás egyes szakaszainak időtartamát, és t₁=0,064 s, t₂=0,197 s, t₃=0,305 s és t₄=0,130 s értékeket kaptam, amelyek jól egyeztek az elmélet alapján számolt értékekkel. A legérdekesebbnek a tömegközéppont mozgását találtam. Képzeld el ..." A levél itt megszakadt. Próbált meg befejezni az alábbi kérdéseknek megfelelően:

a) Ábrázold a rendszer tömegközéppontjának sebességét az idő függvényében!

b) Mekkora a tömegközéppont sebessége a mozgás egyes szakaszainak végén?

Wiedemann László (Budapest) feladata nyomán

Olimpiai válogatóverseny, Sopron, 1998.

A helyesbített feladat megoldása a jelen szám feladataival együtt pótlólag beküldhető.

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. február 11.