Matematikából kitűzött gyakorlatok és feladatok
1999. január

Általános iskolásoknak javasolt feladatok: C. 525, C. 528, Gy. 3246, Gy. 3252.

A pontversenyben kitűzött C gyakorlatok

C. 525. A ,,marslakóknál" egy év hossza 687 nap. A hónapok marslakó-emlékezet óta 26 és 29 naposak. A Mindenáron Újítók azt javasolják, hogy térjenek át 27 és 31 napos hónapokra. A Nyírbálók támogatásával ezt el is fogadtatják, akik azt remélik, hogy ilymódon a hónapok számát (és ezáltal a béreket is) csökkenteni lehet. Nyélbeüthető-e Nyírbálóék elképzelése?

C. 526. Hány olyan 9-cel osztható 7-jegyű szám van, amelynek utolsó előtti számjegye 5?

C. 527. Egy trapéz alakú tó párhuzamos partszakaszai 200 m és 100 m hosszúak, a másik két partvonal hajlásszöge ezekhez 90^o és 45^o. A tavat két őr járja körbe azonos irányban és tempóban úgy, hogy a tó kerülete mentén a két körüljárási irányban egyenlő távolságot tartanak egymástól. Mekkora a két őr legnagyobb távolsága légvonalban?

C. 528. Adott a térben három, egy ponton átmenő, egymásra páronként merőleges egyenes. Elhelyezhető-e egy tetszőleges hegyesszögű háromszög úgy, hogy mindegyik egyenesre essen csúcspontja?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. február 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3246. Két játékos a következő játékot játssza egy nxn-es sakktáblán. Minden mezőn egy korong van elhelyezve, amelynek egyik oldala piros, a másik kék. A játékosok felváltva lépnek. Aki éppen lép, kiválaszt egy kék korongot, és abban a téglalapban, amelynek bal felső sarka a kiválasztott korong, jobb alsó sarka az egész tábla jobb alsó sarka, minden egyes korongot megfordít. Az veszít, aki nem tud lépni.

Melyek azok a kiinduló helyzetek, amelyekben a kezdő játékosnak van nyerő stratégiája?

Gy. 3247. Melyik szám nagyobb, 1997^19981999 vagy 1999^19981997?

Gy. 3248. Jelöljön p tetszőleges prímszámot. Keressük meg a

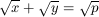
egyenlet összes nem negatív egész megoldását.

Gy. 3249. Adott 2n+1 pozitív páratlan szám, amelyek egyike sem nagyobb, mint 6n. Bizonyítandó, hogy a számok közül valamelyik osztója egy másiknak. (H)

Gy. 3250.  Szabályos ötszögekből egy virágot készítettünk. Az ötszögek csúcsait összekötő szakaszok közül tízet az ábrán látható módon megrajzoltunk. Bizonyítsuk be, hogy az általuk meghatározott tízszög szabályos.

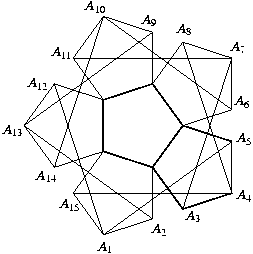
Gy. 3251. Egy háromszög a, b, c oldalaival szemközti szögei 55, 15 és 110 fokosak. Bizonyítsuk be, hogy c²-a²=ab.

Gy. 3252. Tekintsük a térnek azon pontjait, amelyeknek mindhárom koordinátája n-nél nem nagyobb pozitív egész szám. Hány olyan egyenes található, amely ezek közül n pontra illeszkedik?

Gy. 3253. Egy szabályos hatszög keresztmetszetű ceruza lapjai felváltva kék és fehér színűek. Igaz-e, hogy ha ,,messziről" nézzük a ceruzát, akkor ,,ugyanannyi" fehéret és kéket látunk? (H)

Javasolta: Csóka Endre, Debrecen

A pontversenyben kitűzött feladatok

F. 3262. Bizonyítsuk be, hogy a 2²¹⁹⁹⁹-1 számnak van 1999 darab különböző prímosztója.

F. 3263. Legfeljebb hány különböző 3-tagú számtani sorozatot tudunk kiválasztani egy a₁<a₂<...<a_n valós elemű sorozatból?

Amerikai versenyfeladat

F. 3264. Bizonyítsuk be, hogy minden pozitív x-re

.

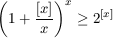F. 3265. Az ABC háromszög BC oldalának felezőpontja legyen F. Mutassuk meg, hogy

ctg FAC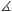-ctg FAB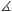=2ctg AFB.

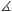Javasolta: Vörös Zoltán, Budapest

F. 3266. Adottak az egyenlő hosszúságú AB és CD szakaszok. AB-t rögzítjük, CD-t pedig úgy mozgatjuk a síkban, hogy az ABCD négyszög AC és BD átlói egyenlőek és állandó hosszúságúak legyenek. Milyen pályát ír le a mozgás során az ABCD négyszög átlóinak metszéspontja?

F. 3267. Ismert, hogy ha egy gömb alakú bolygó felszínén van három ház és három kút, akkor nem tudunk a kutakat és a házakat összekötő, összesen kilenc darab, egymást nem metsző utat építeni. (ld. Reimann István: A geometria és határterületei, 324-325. o. (16.5. tétel).

Igaz-e hasonló állítás, ha a házak és a kutak egy tórusz alakú bolygón vannak?

A pontversenyben kitűzött nehezebb feladatok

N. 195. Két játékos a következő játékot játssza egy nxn-es sakktáblán. Minden mezőn egy korong van elhelyezve, amelynek egyik oldala piros, a másik kék. A játékosok felváltva lépnek. Aki éppen lép, négyféle lépés közül választhat:

• Kiválaszt egy kék korongot és megfordítja;
• Kiválaszt egy kék korongot, és ezt, valamint a vele megegyező sorban, tőle jobbra levő korongok mindegyikét megfordítja;
• Kiválaszt egy kék korongot, és ezt, valamint a vele megegyező oszlopban az alatta levő korongok mindegyikét megfordítja;
• Kiválaszt egy kék korongot, és abban a téglalapban, amelynek bal felső sarka a kiválasztott korong, jobb alsó sarka az egész tábla jobb alsó sarka, minden egyes korongot megfordít.

Melyek azok a kiinduló helyzetek, amelyekben a kezdő játékosnak van nyerő stratégiája?

Kósa Tamás (Budapest) ötletéből

N. 196. Adottak a térben az A, B, C, D, E rácspontok úgy, hogy ABCD egy paralelogramma. Igazoljuk, hogy ha az ABCDE gúla térfogata nagyobb, mint 1/3, akkor tartalmaz a belsejében vagy a határán a csúcsaitól különböző rácspontot.

N. 197. Legyen 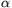tetszőleges 1 és 2 közötti szám, és legyen a_n=[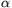ⁿ] (n=0, 1, 2, ...). Igaz-e, hogy véges sok kivétellel bármelyik pozitív egész szám előáll az (a_n) sorozat néhány különböző indexű elemének összegeként?

N. 198. Adott két n pontú teljes gráf, amelyeknek csúcsaiba természetes számokat írtunk, majd minden élre ráírtuk az él két végpontjában lévő számok összegét. Bizonyítsuk be, hogy ha n nem 2-hatvány és a két gráfban az éleken pontosan ugyanazok a számok szerepelnek (mindegyik ugyanannyiszor), akkor ugyanez igaz a két gráf csúcsaira is.

Javasolta: Kiss Tamás, Budapest

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. február 15.