New exercises and problems in Mathematics
March 1999

New exercises for practice in March 1999

C. 533. How does the length of the product of two segments change when the length of the unit segment is doubled?

C. 534. Among the first 539 positive integers, some numbers are chosen so that their sum is not less than one-third the sum of the original numbers. At least how many numbers are chosen?

C. 535. How many (unordered) pairs can be formed from positive integers such that, in each pair, the two numbers are coprime and add up to 285?

C. 536. The whole surface of a sphere of radius R and the curved surface of a cylinder of radius R and height 2R are covered with a coat of paint of the same thickness. Which task requires more paint?

New exercieses in March 1999

Gy. 3262. Given any 3x3 magic square, prove that the sum of the squares of the numbers in the first row equals to the sum of the squares of the numbers in the third row. (A magic square is an nxn array of numbers where the sum of the numbers is the same in each row, each column, and both diagonals of the array.)

Proposer: S. Kiss, Nyíregyháza

Gy. 3263. Consider the whole numbers between 1222 and 1999. Choose, in every possible way, two of them, and take their product. Determine the total sum of these products.

Gy. 3264. Determine those natural numbers k for which 2^2k+3+3^k+2.7^k is divisible by 17.

Gy. 3265. There are given a pair of scales and 12 balls of the same size but of different colours. All of them, apart one, are made of the same substance, the exceptional one having a different density. Is it possible to find the ball which is different from the others based on the result of three measurings? Is it possible to find out, in addition, if this ball is lighter or heavier than the others?

Gy. 3266. In a cyclic trapezium, a, b, c and d denote the common length of the legs, the lengths of the two bases, and the common length of the diagonals, respectively. I claim that d²-a²=bc. Am I right?

Gy. 3267. Circles k₁ and k₂ intersect at points P and Q. Points A and B lie on circles k₁ and k₂, respectively, such that point Q is inside segment AB. Let F denote the midpoint of AB. Let furthermore C and D denote the second intersection points of line PF with the two circles, respectively. Prove that F halves CD, too.

Gy. 3268. In the cartesian system, consider the graphs of the functions y=sin x and y=sin²x. These curves are not just similar, but also homothetic. Find the ratio of the similarity. Where can the centre of the enlargement be?

Gy. 3269. From each one of N towns, a spy is sent to one of the nearest towns. How large can N be if all the spies arrive to only two towns?

New problems in March 1999

F. 3274. Solve the following system of equations:

x+y+z=0
x³+y³+z³=0
x¹⁹⁹⁹-y¹⁹⁹⁹+z¹⁹⁹⁹=2²⁰⁰⁰.

Proposer: T. Nagy, Zalaegerszeg

F. 3275. Find the fraction with the smallest denominator in the open interval .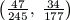

F. 3276.Let A, B, C denote distinct points with integer coordinates in R². Prove that if (|AB|+|BC|)²<8^.[ABC]+1 then A, B, C are three vertices of a square. Here |XY| is the length of segment XY and [ABC] is the area of triangle ABC. 

W. L. Putnam Mathematical Competition, 1998

F. 3277. In a regular pentagon, v₁, v₂, ..., v₅ denote the vectors from the centre to the vertices of the pentagon, respectively. Given that integers k₁, k₂, k₃, k₄, k₅ satisfy k₁v₁+k₂v₂+...+k₅v₅=0, prove that k₁=k₂=...=k₅.

F. 3278. On the points of the curve with equation y=x³, an operation * is defined as follows. Let, for any two points A and B on the curve, A*B denote the reflection of the third intersection point of line AB with the curve about the origin. (If some two points involved in the definition coincide, then the tangent to the curve at the given point is considered instead of the connecting line.) Prove that operation * is associative.

F. 3279. Two straight lines form an angle of 36^o in the plane. A grasshopper is springing to and fro from one line to the other so that the lengths of its jumps are always the same. Prove that it can arrive to at most 10 different points.

New advanced problems in March 1999

N. 203. A quadrilateral ABCD is given in the plane. Circles BCD and ACD cut lines AC and BC at points E and F, respectively. Prove that

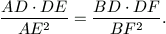
N. 204. A fair die is thrown n times. Find those values of n for which the probability that the total score is divisible by 4 is exactly 1/4.

N. 205. Given an equilateral triangle, determine all those points inside the triangle through which at least 3 different lines, each halving the area of the triangle, can be drawn.

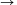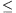N. 206. Determine those continuous functions f:RR for which f(1999)=1000 and which satisfy f(xy)=f(x)f(y)+f(-x)f(-y) and f(x+y)f(x)+f(y) for any real numbers x and y.