 |
Exercises and problems in Physics |
New experimental problem:
m. 206. Measure to what extent perforation decreases the tensile strength of paper. You may use paper perforated in the factory for the experiments (e.g. memo pad), but you can also make perforations with holes at given distances using a sewing-machine. (6 points)
New exercises:
FGy. 3244. How many litres of air does the aerator of a 20-litre aquarium suck in per minute if a bubble spends an average of 2 seconds in the water and a wooden cube with a density of 980 kg/m3 floats in the bubbly water? (3 points)
FGy. 3245. When making soda water, 22 % of the carbon dioxide dissolves in 1 litre of water above which there was initially 2 dl of `empty' space. How many grams of CO2 should there at least be in the cartridge to press the soda out? (4 points)
FGy. 3246. In the morning, at a temperature of 10oC, a tube with a length of 100 cm, closed at one end, is slightly immersed into water in a vertical position, its open end downwards. (The end of the tube touches the water, but the immersion is negligible.) The position of the tube is not changed during the day. In the evening - when the temperature is again 10oC - there is a 5 cm high column of water in the tube.
a) What was the maximum daily temperature?
b) When is the internal energy of the air enclosed in the tube higher: in the morning or at the maximum daily temperature?
The atmospheric pressure is 105 Pa all day and the density of water can be considered as 1000 kg/m3. (4 points)
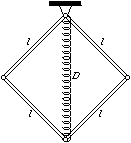 FGy. 3247. The
initially square, jointed system shown in the figure consists of 4
homogeneous rods of length l and mass m and an
unstretched spring with spring constant D. What is the length
of the spring at the equilibrium position of the system? (5 points)
FGy. 3247. The
initially square, jointed system shown in the figure consists of 4
homogeneous rods of length l and mass m and an
unstretched spring with spring constant D. What is the length
of the spring at the equilibrium position of the system? (5 points)
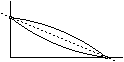 FF. 3248. When does a
skier reach the bottom of the slope more quickly: when the slope is a
convex or a concave circular arc? The radius of the circular arcs is
identical, friction is negligible. (4 points)
FF. 3248. When does a
skier reach the bottom of the slope more quickly: when the slope is a
convex or a concave circular arc? The radius of the circular arcs is
identical, friction is negligible. (4 points)
New problems:
FF. 3249. The maximum power output of a galvanic cell is P and we have 60 such cells. In what arrangements and across what external resistances can exactly 60 P be taken out of them? (4 points)
FF. 3250. Estimate the minimum proportion of a fast neutron beam that can penetrate a 10 cm thick iron plate. (4 points)
FF. 3251. A solid, homogeneous ball of radius r
is spun about a horizontal axis with angular velocity 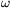 0. The
spinning ball is dropped from height h=
0. The
spinning ball is dropped from height h=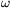 02r2/(2g). The collision number between the
ball and the ground is k, the coefficient of friction is
02r2/(2g). The collision number between the
ball and the ground is k, the coefficient of friction is 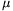 . In what conditions will the ball not roll
yet, but slide and spin when it stops bouncing? (5 points)
. In what conditions will the ball not roll
yet, but slide and spin when it stops bouncing? (5 points)
FF. 3252. What is the stronger limit for the resolution of human eye: the size of the pupil or the density of the neurones in the retina? (5 points)
New advanced problem:
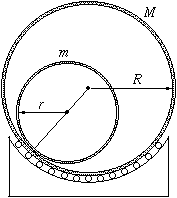 FN. 3253. A tube of
mass M, radius R and with thin walls can revolve freely
about a horizontal axle. Inside, another tube of mass m and
radius r can roll without sliding.
FN. 3253. A tube of
mass M, radius R and with thin walls can revolve freely
about a horizontal axle. Inside, another tube of mass m and
radius r can roll without sliding.
a) How many degrees of freedom does this system have? (How many independent data can describe its position in each instant? b) Chose appropriate co-ordinates and give the equations of motion using them. c) Solve the equations in the case when the larger tube is initially at rest and the smaller one is moving at a low velocity at its bottom position. (6 points)
Bonus problem (April special): Can we experience 10 Sundays in February in a year?

