Fizikából kitűzött gyakorlatok és feladatok 1999. április

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

m. 206. Mérjük meg, hogy a perforálás milyen mértékben csökkenti a papír szakítószilárdságát! Kísérleteinkhez használhatunk gyárilag perforált papírt (pl. jegyzettömböt), de magunk is előállíthatunk megadott lyuktávolságú perforációt egy papírlapon, például varrógéppel. (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

FGy. 3244. Hány liter levegőt szív be percenként a 20 literes akvárium levegőztetője, ha egy buborék átlagosan 2 másodpercig tartózkodik a vízben, és a 980 kg/m³ sűrűségű fakocka éppen lebeg a buborékos vízben? (3 pont)

Közli: Simon Péter, Pécs

FGy. 3245. Szódavíz készítésekor a szén-dioxid 22 %-a oldódik fel az 1 liter vízben, mely felett betöltéskor még 2 dl ,,üres'' tér maradt. Legalább hány gramm CO₂-nek kell lennie a patronban, hogy a szifonból kinyomja a vizet? (4 pont)

Közli: Szilágyi György, Budapest

FGy. 3246. Reggel 10 ^oC hőmérsékleten egy 100 cm hosszúságú, egyik végén zárt csövet függőleges helyzetben nyitott szájával lefelé kissé vízbe süllyesztünk. (A cső vége beleér a vízbe, de a bemerülés elhanyagolható.) Napközben a cső helyzetét nem változtatjuk. Este - amikor ismét 10 ^oC a hőmérséklet - azt látjuk, hogy a csőben 5 cm magasan áll a víz.

a) Mekkora volt az aznapi csúcshőmérséklet?

b) Mikor nagyobb a csőbe zárt levegő belső energiája, reggel vagy az aznapi csúcshőmérsékleten?

A légköri nyomás mindvégig 10⁵ Pa, a víz sűrűségét tekinthetjük 1000 kg/m³-nek. (4 pont)

Közli: Szegedi Ervin, Debrecen

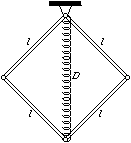FGy. 3247. Az ábrán látható, kezdetben négyzet alakú csuklós szerkezet 4 darab l hosszúságú, m tömegű homogén rúdból és egy nyújtatlan, D direkciós állandójú rugóból áll. Mekkora a rugó hossza a rendszer egyensúlyi helyzetében? (5 pont)

Közli: Varga István, Békéscsaba

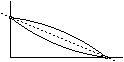FF. 3248. Mikor ér hamarabb a lejtő aljára a síelő: ha a domború, vagy ha a homorú körív alakú lejtőn siklik le? A két körív sugara ugyanakkora, a súrlódás elhanyagolható. (4 pont)

Közli: Lang Ágota, Sopron

FF. 3249. Egy galvánelem maximálisan P teljesítményt tud leadni, és van 60 darab ilyen galvánelemünk. Az elemek milyen kapcsolásai esetén és mekkora külső ellenállásokon vehető ki belőlük pontosan 60 P teljesítmény? (4 pont)

Közli: Radnai Gyula, Budapest

FF. 3250. Becsüljük meg, hogy egy gyors neutronokból álló részecskenyalábnak legalább hányad része hatol át egy 10 cm vastag vaslemezen! (4 pont)

Közli: Radnóti Katalin, Budapest

FF. 3251. Egy r sugarú tömör, homogén golyót 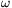₀ szögsebességgel megpörgetünk vízszintes tengely körül. A pörgő golyót h=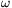₀²r²/(2g) magasságból elejtjük. A golyó és a talaj közti ütközési szám k, a súrlódási együttható 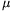. Mi a feltétele annak, hogy a pattogás megszűnése után még ne gördüljön a golyó, hanem csúszva forogjon? (5 pont)

Közli: Szabó Szilárd, Budapest

FF. 3252. Mi korlátozza inkább az emberi szem felbontóképességét: a pupilla nagysága, vagy a retina idegsejtjeinek sűrűsége? (5 pont)

Közli: Kedves Ferenc, Budapest

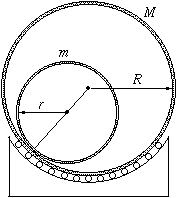FN. 3253. Egy M tömegű, R sugarú, vékonyfalú cső vízszintes tengely körül szabadon foroghat. A belsejében csúszásmentesen gördülhet egy m tömegű, r sugarú másik cső.

a) Hány szabadsági fokú ez a rendszer? (Hány független adattal jellemezhető pillanatról pillanatra a helyzete?)

b) Válasszunk alkalmas koordinátákat, és adjuk meg az ezekre vonatkozó mozgásegyenleteket !

c) Oldjuk meg az egyenleteket olyan esetben, amikor kezdetben a nagyobb cső áll, a kisebb pedig a legmélyebb helyzetében kicsiny sebességgel mozog. (6 pont)

Közli: Gnädig Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. május 11.