New exercises and problems in Mathematics
April 1999
 |
New exercises for practice in April 1999 |
C. 537. Working on his essay during class, Sam glanced at his watch and noticed that the time that had already passed was five times more than that still was left. After M minutes had passed the ratio was already 8. Find out what the ratio was after another M minutes had passed.
C. 538. Find those (not necessarily positive) prime numbers p for which each of the following expressions is a prime: 2p+1, 4p+1 and 6p+1.
Proposer: Á. Kovács, Budapest
C. 539. Prove that in any acute isosceles triangle
AM=a/tan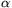 holds,
where, conventionally, a denotes the base of the triangle, A
and
holds,
where, conventionally, a denotes the base of the triangle, A
and 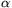 , respectively, denote the
vertex and the angle opposite to it, and M is the orthocentre.
, respectively, denote the
vertex and the angle opposite to it, and M is the orthocentre.
C. 540. A half ball of radius 10 cm emerges from
level plane (for the great annoyance of the motorists). A cylinder
rolls on the plane until its lateral surface hits the half ball. Let
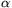 denote the angle the common
tangent plane of the two objects forms with the horizontal
plane. Given that
denote the angle the common
tangent plane of the two objects forms with the horizontal
plane. Given that 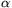
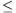 30o, find the minimum
possible radius of the cylinder.
30o, find the minimum
possible radius of the cylinder.
 |
New exercieses in April 1999 |
Gy. 3270. Let n>2 be an even number. Prove
that 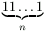 is not a prime in any number
system.
is not a prime in any number
system.
Proposer: Á. Kovács, Budapest
Gy. 3271. Which fraction is the larger: 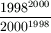 or
or 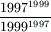 ?
?
Proposer: J. Bíró, Budapest
Gy. 3272. The edges a, b, c of a certain cuboid are integers, moreover, its surface area and its volume measure the same. Given that c=ab/2, determine the edges of the cuboid.
Proposer: Á. Kovács, Budapest
Gy. 3273. Prove that 512+210 is a composite number.
St. Petersburg, Mathematical Olimpiad
Gy. 3274. We have three congruent right-angled triangle shaped pieces of paper. We may cut any of these into two parts along its altitude. We may repeat this procedure for the new set of pieces, and so on. Provided that no matter how we choose the procedure there always will be two congruent triangles, determine the ratio between the legs of the triangles.
Gy. 3275. In a certain quadrilateral, each diagonal halves the area of the quadrilateral. Prove that they together partition the quadrilateral into four parts of equal area.
Gy. 3276. Centre O of a circle k2 lies on the circumference of circle k1, of radius r. The circles intersect at points A and B, moreover, a point S lies inside k1. Line BS intersects k1 at point T, different from B. Given that the triangle AOS is equilateral, prove that TS=r.
Gy. 3277. Let a and b denote
positive integers. Given a segment of length 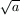 , describe how to construct an other segment of length
, describe how to construct an other segment of length
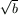 .
.
Proposer: Á. Kovács, Budapest
 |
New problems in April 1999 |
F. 3280. Prove that, if x1, x2, ..., xn are arbitrary positive numbers, then
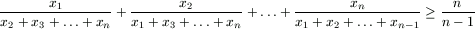 .
.
F. 3281. A piece of chocolate is divided into smaller pieces. In each step the largest piece - or one of them if this piece is not unique - is broken into smaller parts in such a way that none of the new parts exceed the half of the piece just broken. Prove that after the kth step each piece is smaller than the 2/(k+1)th part of the whole chocolate.
Lovász László, Budapest
F. 3282. Find the range of the expression x2+2xy, provided that x2+y2=1.
F. 3283. In a set of 2000 segments, each segment is at least 1 unit long. It is not possible, moreover, to construct a closed polygon from any subset of this set of segments. Prove that the total length of the segments is at least 21999.
F. 3284. In a triangle ABC, a point P
satisfies 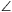 PAB=
PAB=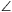 PBC=
PBC=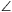 PCA=
PCA=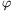 . If the
angles of the triangle are denoted by
. If the
angles of the triangle are denoted by 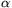 ,
, 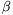 and
and 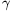 , prove that
, prove that
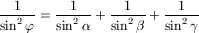 .
.
F. 3285. A circle k and a point P outside the circle are given in the plane. Determine the locus of the centre of a circle which is obtained as the intersection of a sphere that contains k and a right circular cone with apex P.
 |
New advanced problems in April 1999 |
N. 207. A continuous function
f:[0,1] [0,1]
has the following property: for any real number x
[0,1]
has the following property: for any real number x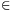 [0,1], the sequence
f(x), f(f(x)),
f(f(f(x))), ... contains 0. Does it follow
that, for n large enough,
[0,1], the sequence
f(x), f(f(x)),
f(f(f(x))), ... contains 0. Does it follow
that, for n large enough, 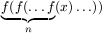 is
identically 0?
is
identically 0?
N. 208. Assume that p is a prime number greater than 2. Prove that there exists a prime q<p such that qp-1-1 is divisible by p2.
N. 209. Find 6 points in the plane such that any two of them are at an integer distance apart, no three of them are collinear, and no four lie on the same circle.
N. 210. Prove that any closed space curve contains four coplanar points. Is it always true that it contains five coplanar points, too?
Proposer: S. Róka, Nyíregyháza

