Matematikából kitűzött gyakorlatok és feladatok
1999. május

Általános iskolásoknak javasolt feladatok: C. 541., C. 543., Gy. 3278., Gy. 3281.

A pontversenyben kitűzött C gyakorlatok

C. 541. Egy hatoldalas házi dolgozatban négy ábrát kell elhelyeznünk. Az ábrák sorrendje meghatározott és egy oldalon legfeljebb két ábra lehet. Hányféleképpen tehető ez meg? (Az ábrák egy-egy oldalon belüli helyzetére nem vagyunk tekintettel.)

C. 542. Milyen pozitív egész n-ekre teljesül az

(n-2)(2+2²+...+2ⁿ)<n^.2ⁿ

egyenlőtlenség?

C. 543. Szerkesszünk háromszöget, ha adott egy szöge és két magassága.

C. 544. ,,Szerkezetkész'' egységkockánknak van alap- és fedőlapja, továbbá oldalélei. A fedőlapot az alaplaphoz képest 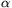hegyesszöggel elcsavarjuk a két lap középpontját összekötő egyenes mint tengely körül. Mennyivel kerül közelebb a fedőlap az alaplaphoz, ha az oldalélek hossza nem változik és a csúcsok összeköttetése is megmarad?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. június 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3278. Egy 3x3-as bűvös négyzet ábra szerinti három eleme, a, b és c adott. Határozzuk meg a hiányzó elemeket (minden sorban, minden oszlopban és a két átlóban a számok összege ugyanannyi).

Dr. Kiss Sándor (Nyíregyháza) ötlete alapján

Gy. 3279. Tíz gyerek ,,bogozódós'' játékot játszik: körbe állnak, és csukott szemmel, kinyújtott kézzel elindulnak a kör közepe felé. Mindenki mindkét kezével megfogja valaki másnak a kezét. Ezután kinyitják a szemüket, és elkezdenek ,,kibogozódni'': átbújnak egymás keze alatt, átlépik egymás kezét stb. (mindenki kellően hajlékony) - de nem engedik el közben egymás kezét. Az összes eset hány százalékában igaz, hogy ha egy helyen két szomszédos gyerek elengedi egymás kezét, akkor a tíz gyerek egymás kezét fogva összefüggő láncot alkot? (H)

Gy. 3280. Legyenek p és q olyan pozitív valós számok, amelyek reciprokainak összege 1. Bizonyítsuk be, hogy

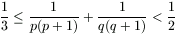és .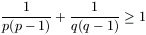

Javasolta: Róka Sándor, Nyíregyháza

Gy. 3281. Egy téglatest egy csúcsba futó éleinek mérőszámai prímszámok, felszínének mérőszáma prímhatvány. Bizonyítsuk be, hogy az élei közül pontosan az egyik 2^k-1 alakú prímszám.

Javasolta: Kovács Ádám, Budapest

Gy. 3282. Egy háromszög három oldala a, b és c. Bizonyítsuk be, hogy

.

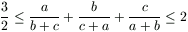Lehetséges-e egyenlőség?

Gy. 3283. Egy derékszögű háromszög egyik befogójára és átfogójára négyzetet rajzoltunk kifelé, és megszerkesztettük az M pontot az 1. ábrának megfelelően. Bizonyítsuk be, hogy M rajta van a háromszög beírt négyzetének kerületén (2. ábra).

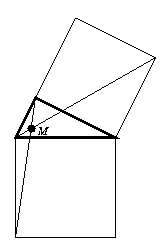1. ábra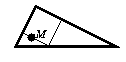

2. ábra

Javasolta: Herczeg János, Budapest

Gy. 3284. Igazoljuk, hogy ha egy körív felezi egy k kör területét, akkor hossza nagyobb k átmérőjénél. (H)

Gy. 3285. Milyen rombuszhoz létezik két különböző paralelepipedon, amelyeknek a lapjai egybevágóak ezzel a rombusszal?

Javasolta: Peták Kálmán, Szolnok

A pontversenyben kitűzött feladatok

F. 3286. A t milyen értékeire asszociatív a pozitív számokon értelmezett kétváltozós 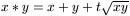művelet?

F. 3287. Egy halmaz páronként diszjunkt halmazokra való felbontását a halmaz egy partíciójának nevezzük. Igazoljuk, hogy egy n elemű halmaznak legfeljebb n! darab partíciója van.

Javasolta: Róka Sándor, Nyíregyháza

F. 3288. Legyenek n és k pozitív egészek és p prímszám úgy, hogy p^k|n!. Bizonyítsuk be, hogy ekkor n! osztható (p!)^k-nal is.

F. 3289. Adott egy P pont és az a, b, c szakaszok. Szerkesszünk olyan szabályos háromszöget, amelynek a csúcsait P-vel összekötő szakaszok hossza éppen a, b és c.

F. 3290. Mutassuk meg, hogy az A(1, 0, 2), B(4, 3, -1), C(0, 3, -1), D(5, -2, 4) koordinátájú pontok egy síkban vannak. Mekkora a négy pont által meghatározott konvex négyszög területe?

F. 3291. Bizonyítsuk be, hogy bármely egyenlő oldalú rácssokszög oldalszáma páros.

Javasolta: Ruzsa Z. Imre, Budapest

A pontversenyben kitűzött nehezebb feladatok

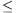N. 211. Hány olyan n-elemű, pozitív egész számokból álló sorozat van, amelyben tetszőleges 1in esetén az i-nél nagyobb elemek száma legfeljebb n-i?

N. 212. Melyek azok az a és n pozitív egész számok, amelyekre 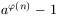mindegyik prímosztója osztója n-nek is?

N. 213. Legyen p_n(x)=a_n,0+a_n,1x+...+a_n,nxⁿ az a legfeljebb n-edfokú polinom, amelynek értéke a 2⁰, 2¹, ..., 2ⁿ helyeken rendre 0, 1, ..., n. Határozzuk meg tetszőleges k pozitív egész esetén a 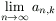határértéket.

N. 214. A sík egy P pontjából két érintőt húzunk az y=x² parabolához. A két érintési pontot jelöljük Q_P-vel és R_P-vel, a parabola Q_P és R_P közötti ívének hosszát pedig l(Q_P, R_P)-vel. Melyek azok a P pontok, amelyekre PQ_P+PR_P-l(Q_P, R_P) állandó?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. június 15.