Matematikából kitűzött gyakorlatok és feladatok
1999. szeptember

Figyelem! A pontverseny feltételei a tavalyi évhez képest megváltoztak. Kérjük, olvassa el a versenykiírást!

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 545. Egy teli tubusban 75ml fogkrém van. Hány méter fogkrémet lehetne belőle kinyomni, ha tudjuk, hogy a kinyomott fogkrém keresztmetszetének átmérője 6 mm?

C. 546. Valaki leírta az egész számokat egymás mellé 1-től 1999-ig. Milyen számjegy áll az 1999-edik helyen?

C. 547. Egy óra nagy-, kis- és másodpercmutatója közös tengelyen van. 12 órakor fedik egymást. Legközelebb mikor lesz fedésben a három mutató?

C. 548. Az y(x²+y²)-x(x²+y²)-y+x=0 egyenlettel adott ponthalmaz melyik pontja van legközelebb a P(3;4) ponthoz?

Javasolta: Bánhegyi László, Budapest

C. 549. Az egységnyi élű ABCDEFGH kocka BE lapátlójának E-hez közelebbi harmadolópontja milyen távol van a CFH háromszög síkjától (lásd az ábrát)?

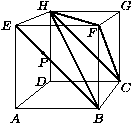
Javasolta: Bánhegyi László, Budapest

A B pontversenyben kitűzött feladatok

B. 3292. A család a két gyerekre bízta a felújítandó konyha kövének kiválasztását. Egyiküknek a baloldalon, másikuknak a jobboldalon látható színezés tetszik jobban. Végül úgy döntenek, azt választják, amelyikben több a barna szín. Melyiket választották? (3 pont)

 

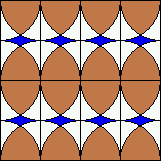
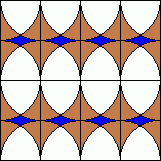
B. 3293. Az a és b pozitív egész számokra teljesül, hogy 34a=43b. Mutassuk meg, hogy a+b összetett szám. (3 pont)

Javasolta: Róka Sándor, Nyíregyháza

B. 3294. A táblára felírtuk az 1, 2, 3, ..., 20 számokat. Letörlünk közülük két számot, a-t és b-t, s helyettük felírjuk az ab+a+b számot. Ezt az eljárást 19-szer elvégezve milyen szám maradhat a táblán? (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

B. 3295. Egy háromszög súlypontján átmenő egyenesek közül melyek felezik a háromszög területét? (4 pont)

Javasolta: Bogdán Zoltán, Cegléd

B. 3296. Baloldalt egy sáska, középen egy szöcske, jobboldalt egy tücsök ül egy hosszú, egyenes árokban. Időnként valamelyik átugorja egyik szomszédját. Előfordulhat-e, hogy 1999 ugrás után a kiinduló sorrendben ülnek, ha végig csak az árokban (egy egyenes mentén) ugrálnak? (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

B. 3297. Egy derékszögű háromszög befogói a és b, átfogója c. Bizonyítsuk be, hogy 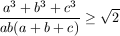. (4 pont)

Javasolta: Paulovics Illés

B. 3298. Egy háromszög alapú gúla oldalélei egységnyi hosszúságúak, az oldalélek által bezárt szögek 60^o, 90^o illetve 120^o. Mekkora a gúla térfogata? (4 pont)

Javasolta: Vajda Szilárd, Kolozsvár

B. 3299. Egy R sugarú kerek asztalon elhelyeztünk n darab r sugarú pénzérmét úgy, hogy minden érme egy teljes lapjával az asztalon fekszik. Az asztalra újabb érme már nem helyezhető el. Mutassuk meg, hogy 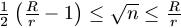. (5 pont)

Javasolta: Róka Sándor, Nyíregyháza

B. 3300. Egy konvex poliéder egyik lapjának csúcsait pirosra, a többi csúcsot pedig kékre színeztük. Bizonyítsuk be, hogy van olyan kék csúcs, amelyből legfeljebb 5 él indul ki, vagy pedig van olyan piros csúcs, amelyből legfeljebb 3 él indul ki. (5 pont)

B. 3301. Egy H halmaz elemeinek száma: |H|=n. Mutassuk meg, hogy

.

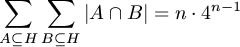(5 pont)

Javasolta: Róka Sándor, Nyíregyháza

A pontversenyben kitűzött nehezebb feladatok

A. 215. A P, Q és R pontok úgy helyezkednek el az O középpontú 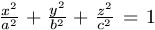egyenletű ellipszoidon, hogy az OP, OQ, OR szakaszok páronként merőlegesek egymásra. Mutassuk meg, hogy a PQR sík és O távolsága nem függ P, Q, és R megválasztásától.

Jugoszláv versenyfeladat

A. 216. Bizonyítsuk be, hogy tetszőleges n pozitív egészhez létezik olyan legfeljebb n-edfokú, egész együtthatós p polinom, hogy páros x egész szám esetén p(x) osztható 2ⁿ-nel, páratlan x esetén pedig p(x)-1 osztható 2ⁿ-nel.

Javasolta: Hajnal Péter, Szeged

A. 217. Az a₁, a₂, ..., a_n pozitív egészek legnagyobb közös osztója 1, és közülük bármelyik kettőnek ugyanaz a legkisebb közös többszöröse. Bizonyítsuk be, hogy létezik egy olyan p egész szám, hogy tetszőleges u egész szám esetén u és p-u közül pontosan az egyik írható fel a₁x₁+a₂x₂+...+a_nx_n alakban, alkalmas x₁, ..., x_n nemnegatív egészekkel.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. október 15.