 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 209. Stand dominoes parallel to each other and at even distances in such a way that pushing the first one makes all of them tumble over. Investigate what the speed of the tumbling wave depends on, and how. (6 points)
New problems:
P. 3274. The light of a searchlight placed at the top of a 26 meter high lighthouse standing on the seashore could first be seen at 30 km from the shore, through the telescope of a ship. How high was the telescope above the surface of the sea? (4 points)
P. 3275. How deep should a floating wooden log be submerged
into water so that the work done during the submerging is equal to the
minimum work necessary to lift the log out of the water? The density
of wood is k times smaller than that of water. Investigate the
case when k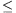
2. (4 points)
P. 3276. Make an estimate of the universal gas constant using the following measurement data made on 100 oC steam.
| p (Pa) | 986 | 9806 | 98066 |
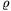 (kg/m3) | 0,00570 | 0,05705 | 0,578 |
P. 3277. Starting from the edge of a rock, Tarzan swings towards another rock on a 18 m long liana. The bottom of his trajectory is 3 metres lower than his starting point. Will the liana support the jump of Tarzan, who weighs 900 N, if its maximum tensile strength is 1200 N? (4 points)
P. 3278. Should two resistors of different resistances but identical maximum power be connected in series or in parallel so that their power is maximum together? (4 points)
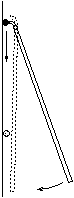P. 3279. One of the devices
used to measure gravitational acceleration is Whiting's plank
pendulum. Show that a ball in free fall starting together with the
plank from the rotational axis of the plank always hits the plank at
the same proportion of the length of the latter, regardless of the
actual length. What is this proportion? (4 points)
P. 3280. Should the volume of air saturated with steam be decreased or increased in order to condense some of the water from the air? (4 points)
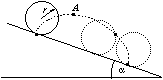P. 3281. Determine the radius
of curvature at the topmost point of the trajectory described by a
point of a hoop rolling without sliding on a slope. (5 points)
P. 3282. A circular conductor of radius R is electrically charged with charge Q. How does the electric field strength change along the straight line crossing the centre of the circle and perpendicular to the plane of the circle? Where does it reach its maximum value? (5 points)
P. 3283. The suspension springs of all the wheels of a car are identical. How much does the body of the car (considered as rigid) rise above the wheels when the car is parked on a 8 cm high kerb with its right front wheel? How does the result change when the car is parked with both its right wheels on the kerb? Does the result depend on the number and the position of the persons sitting in the car? (6 points)