Matematikából kitűzött gyakorlatok és feladatok
1999. november
Figyelem! A pontverseny feltételei a tavalyi évhez képest megváltoztak. Kérjük, olvassa el a versenykiírást!
 |
A C pontversenyben kitűzött (könnyebb) gyakorlatok |
C.555. Melyik az a legkisebb egész szám, amelyik kétféleképpen is felírható két különböző pozitív négyzetszám összegeként?
C.556. Egy öt fordulóból álló futóverseny sorozaton 50 induló vett részt. Bandi minden egyes fordulóban a 10. helyen végzett. A verseny végeredményét az egyes fordulóban elért időeredmények összeadásával határozzák meg. Előfordulhatott-e, hogy az összetett versenyben Bandi
- a) az első
b) az utolsó helyen végzett?
C.557. Igazoljuk, hogy nem létezik olyan egymást követő, pozitív páratlan számokból álló legalább két elemű számsorozat, amelynek összege prímszám.
Javasolta: Vajda Szilárd, Kolozsvár
C.558. Hány különböző rácsnégyzet jelölhető ki az nxn-es négyzetrácson úgy, hogy oldalai párhuzamosak legyenek a négyzetrács oldalaival?
Javasolta: Bakonyi Gábor, Budapest
C.559. Egy gúlába (csúcsával lefelé tartva) vizet töltünk, így a víz 10 cm magasan áll benne. Nyílását lezárva alaplapjára állítjuk a gúlát, így most 2 cm magasan áll a víz. Milyen magas a gúla?
Javasolta: Koncz Levente, Budapest
 |
A B pontversenyben kitűzött feladatok |
B.3312. Szilveszter észrevette, hogy ha születési évének számjegyeit összeadja, azt a számot kapja, amely nagyapja születési évszámának utolsó két jegyéből áll. Szilveszter születési évszámának utolsó két jegye összeolvasva pedig nagyapja jelenlegi életkora. Hány éves Szilveszter? (3 pont)
Javasolta: Nyul Balázs 9. o. t., Debrecen
B.3313. Az ABCD rombuszt a BD átlója két
szabályos háromszögre vágja. Az AD szakaszon adott egy P,
a CD szakaszon pedig egy Q pont úgy, hogy a
PBQ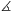
=60o. Mekkora a PBQ háromszög másik két
szöge? (3 pont)
B.3314. Meg lehet-e számozni egy szabályos oktaéder éleit az 1, 2,..., 12 számokkal úgy, hogy mindegyik csúcsban ugyanannyi legyen az oda befutó élekre írt számok összege? (3 pont)
Javasolta: Reményi Gusztáv, Budapest
B.3315. Adjuk meg azt az f(x)=ax alakú függvényt, amely a g(x)=x2 függvényt "jól" közelíti az x=0,1; 0,2; ...;0,5 helyeken abban az értelemben, hogy az ezeken a helyeken számított |f(x)-g(x)| hibák közül a legnagyobbik a lehető legkisebb. (4 pont)
Javasolta: Bakonyi Gábor, Budapest
B.3316. Legyen P az ABC háromszög egy belső pontja. Az AP és a BP egyenesek messék a háromszög szemközti oldalát a D illetve az E pontban. Mutassuk meg, hogy ha AP=BP és BE=CE, akkor 1/AP=1/AD+1/AC. (4 pont)
Javasolta: Lee, Ho-joo, Korea
B.3317. Oldjuk meg a következő egyenletet:
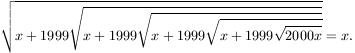
(4 pont)
Javasolta: Hans Zoltán, Nagykanizsa
B.3318. Az egységnyi sugarú k1 és k2 körök a P pontban érintik egymást. A két kör egyik P-n át nem menő közös érintője az e egyenes. Legyen i>2 esetén ki az a ki-2-től különböző kör, amely érinti k1-et, ki-1-et és e-t. Határozzuk meg k1999 sugarát. (5 pont)
B.3319. Ismert, hogy egy adott körbe írható négy csúcsú síkidomok közül a négyzet területe a legnagyobb. Igaz-e, hogy egy adott gömbbe írható nyolc csúcsú testek közül a beírható kocka térfogata a legnagyobb? (4 pont)
B.3320. Oldjuk meg a következő egyenletet:
xx1/2=1/2.
(5 pont)
Javasolta: Lovrics László, Budapest
B.3321. Legyen K egy konvex sokszög. Mutassuk meg, hogy elhelyezhető a síkon 6 darab K-val egybevágó sokszög úgy, hogy ezek mindegyikének van K-val közös határpontja, de a hét sokszög közül semelyik kettőnek nincs közös belső pontja. (5 pont)
 |
A pontversenyben kitűzött nehezebb feladatok |
A.221. Legyenek az N négyzet csúcsai a (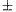
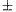1999; 1999) koordinátájú pontok, a H háromszög
csúcsai pedig (-1; 0), (0; -1) és (1; 1). A H háromszögnek
legfeljebb hány egymásba nem nyúló, eltolt példányát lehet elhelyezni
az N négyzetben?
Javasolta: Pap Gyula, Debrecen
A.222. Az a,b,c egész számok legnagyobb közös osztója 1. Az (a,b,c) számhármast más számhármasokra cserélhetjük úgy, hogy minden lépésben az egyik számot növeljük vagy csökkentjük a számhármas egy másik elemének valamilyen többszörösével. Igaz-e, hogy az a,b,c számok megválasztásától függetlenül, legfeljebb 10 lépésben eljuthatunk az (1,0,0) számhármashoz?
Javasolta: Abért Miklós, Budapest
A.223. Keressük meg az összes olyan f:R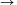
R függvényt, amelyre
f(x-f(y))=f(x+y1999)+f(f(y)+y1999)+1
teljesül tetszőleges x,y valós számok esetén.
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)