 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 212. Determine the frequency of the fundamental tone created by clinking two empty goblets.
New problems:
P. 3304 Two metal rods of identical cross section but different length and material properties are glued together. The rod obtained this way is hung up by two long and vertical ropes fixed to its end points. In which direction will the point of contact of the two rods be displaced upon increasing the temperature?
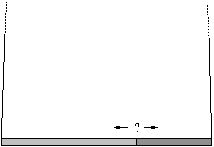
P. 3305 Determine the average spacing between cars of a row proceeding at 60 km/h, if the driver of a car travelling at 80 km/h in the opposite direction passes by 14 cars of the row per kilometre. (The average length of the cars is 5 m.)
P. 3306 Going downhill on a long 30o slope, a skier of mass 80 kg reaches a terminal speed of 30 m/s, i.e.\ after a while he travels at this constant speed. He did not use his sticks to accelerate, thus the first 2 metres took him 1 second. How much snow would melt under his skis per minute if all the heat produced by friction were used to melt the snow? What forces act on the skier, and how large are they?
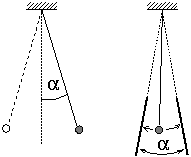
P. 3307 A simple pendulum swings with an initial
angular amplitude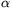 
. How does the
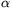period of swinging change if two elastic walls making an angle are introduced in the system in a
symmetrical way as shown in the figure?
P. 3308 A four-wheel drive car arrives at the
bottom of an icy slope of angle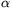
with a speed v. How high can it go up if the coefficient of
friction is 
?
P. 3309 Two bodies connected vertically by a length of rope are attached to the free end of a vertical coiled spring as shown in the figure. If the rope snaps, the body staying on the spring starts to oscillate. If the two bodies are interchanged and then the rope snaps, the body staying on the spring starts to oscillate again. The difference of the two periods of oscillation is 0.3 sec. Determine the period of oscillation in each case if the two bodies together oscillate with a period of 1.5 sec on the same spring.
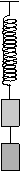
P. 3310 A battery is connected to a linear variable resistor between one end and the sliding contact of which a load resistor is placed. a) What is the maximum attainable power across the load resistor? b) Determine the position of the sliding contact if the power across the load resistor is half of the maximum value.
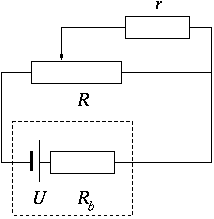
Use the following data: U=12 V, Rb=1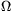 
, R=120 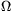, r=25 .
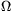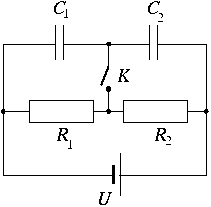
P. 3311 Will the total electrostatic energy of the capacitors in the figure increase, decrease, or stay unchanged if switch K is closed?
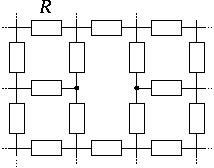
P. 3312 Each edge of an infinite grid has resistance R. One edge between two adjacent grid points is removed. Determine the resultant resistance between these two points.
P. 3313 Part of the series of isotopes produced by the decay of thorium-232, together with the corresponding half-lives, is given below.
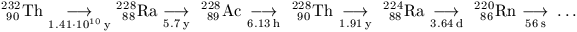
Thorium-232 and thorium-228 in equilibrium are extracted from an ore and purified by a chemical process. Sketch the form of the variation in the number of atoms of radon-220 you would expect to be present in 10-3 kg of this material over a (logarithmic) range from 10-3 years to 103 years.
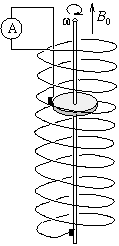
P. 3314. A metal
disc of radius r can rotate with negligible friction inside a
long, straight coil, about a shaft parallel to the symmetry axis of
the coil. One end of the wire of the coil is connected with a sliding
contact to the edge of the disc and the other one to the shaft. The
ohmic resistance of the coil is R and there are n turns
on a unit length of it. The coil is placed so that its axis is
parallel to the induction vector B0 of the Earth. What current flows through the
ammeter if the disc rotates with angular frequency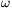 
? Plot the current as a function of
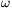for both directions of the
rotation. Prove that the work necessary to spin the disc is identical
to the Joule heat released on the ohmic resistance of the coil.
