New exercises and problems in Mathematics
January 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in January 2000 |
C. 565. Ten eggs are broken up into a bowl, one after the other. Two of them are bad, but this turns out only when they are being broken up, so they spoil those eggs already in the bowl. Thus, when a bad egg is found, the bowl is washed up, and the procedure is continued with the remaining eggs. What proportion, on the average, of the good eggs get wasted?
C. 566. Solve the following equation:
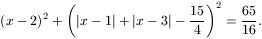
C. 567. The lengths of the edges of a rectangular box are all integers. Its volume, half of its surface area, and the lengths of its edges starting at the same vertex add up to 2000. Determine the lengths of the edges of the box.
C. 568. How many different ways are there to select 5 out of the first 90 positive integers so that they form a) an arithmetic b) a geometric progression?
C. 569. Determine those points of the line y=x from which one can draw two perpendicular tangents to the parabola y=x2.
 |
New problems in January 2000 |
B. 3332. The first n positive integers are to be arranged around a circle in such a way that the sum of any two consecutive numbers is divisible by the next one in clockwise order. Find those values of n for which this can be done. (3 points)
Tournament of Towns, 1999.
B. 3333. How many faces of an icosahedron can be chosen without any two of them sharing a common edge? (3 points)
B. 3334. Prove that there is exactly one number system in which there exists a 3-digit number twice as large as the number it represents in the decimal system. (4 points)
JavasoltaProposedBy: N. Gyanta, Budapest
B. 3335. A pentagon K and another polygon L are given in the plane such that neither of them has a vertex on any line that contains a side of the other. Find the maximum number of intersection points their sides can form, assuming that a) L is a triangle b) L is a quadrilateral. (5 points)
B. 3336. An equilateral triangle is rotated around its center, in counterclockwise direction, by 3o. Next, it is rotated further by another 9o, then by 27o, and so on, by 3k degrees in the kth step. How many different positions are occupied by the triangle during such a procedure? (3 points)
B. 3337. Given the focus and two points of a parabola, construct its directrix. (3 points)
B. 3338. Solve the following system of equations:
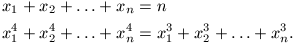
(4points)
JavasoltaProposedBy: M. Ábrány,Ukrajna
B. 3339. Prove that, in any spherical triangle, the three medians meet at a common point. (4 points)
B. 3340. When rolling a die 12 times, which of the following two is more probable: a) at least one of the first 6 scores is 6, b) at least two of all the 12 scores are 6? (4 points)
B. 3341. In a triangle ABC, D denotes the foot of the perpendicular dropped from A. The pairwise distinct points D, E and F lie on the same line, moreover, AE and AF are perpendicular to BE and CF, respectively. The midpoints of segments BC and EF are denoted by M and N. Prove that AN is perpendicular to MN. (5 points)
Problem of the 10th Asian Mathematical Olympiad
 |
New advanced problems in January 2000 |
A. 227. Is there a positive integer n such that, every digit, different from 0, appears the same number of times in the decimal form of each of the numbers n, 2n, 3n, ..., 2000n?
A. 228. Let Q denote the set of rational
numbers. Suppose that the functions f, g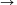: Q
Q are strictly monotone
increasing functions which attain every rational value. Is it
necessarily true that the range of values of the function
f+g is also the whole set Q?
E. Fried, Budapest
A. 229. Two pentagons are given in the plane such that neither of them has a vertex on any line that contains a side of the other. Find the maximum number of intersection points their sides can form.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.