Matematikából kitűzött gyakorlatok és feladatok
2000. január

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 565. Egy tálba egymás után felütünk tíz darab tojást. A tojások közül kettő romlott, de ez csak a feltöréskor derül ki. A záptojások az összes előttük feltört tojást használhatatlanná teszik. A tálat ilyenkor kimossuk és a megmaradt tojásokkal folytatjuk az eljárást. A jó tojásoknak átlagosan hányadrésze megy ilymódon veszendőbe?

C. 566. Oldjuk meg a következő egyenletet:

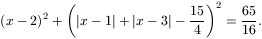
C. 567. Egy téglatest minden élének mérőszáma egész. A téglatest térfogatának, fél felszínének és az egyik csúcsba befutó élek hosszának mérőszámait összeadva 2000-et kapunk. Mekkorák a téglatest élei?

C. 568. Az ötös lottó sorsolásnak hány olyan különböző kimenetele lehetséges, amelynél a nyerő számok a) számtani b) mértani sorozatot alkotnak?

C. 569. Az y=x² parabolához az y=x egyenletű egyenes mely pontjából húzható két, egymásra merőleges érintő?

A B pontversenyben kitűzött feladatok

B. 3332. Az első n pozitív egész számot egy kör kerületén úgy szeretnénk elhelyezni, hogy bármely két szomszédos szám összege osztható legyen az óramutató járása szerint közvetlenül utánuk álló számmal. Milyen n-re lehetséges ez? (3 pont)

Tournament of Towns, 1999.

B. 3333. Egy ikozaéder néhány lapját pirosra festjük úgy, hogy két befestett lapnak nincs közös éle. Maximálisan hány lap festhető be ezzel a feltétellel? (3 pont)

B. 3334. Bizonyítsuk be, hogy egyetlen olyan számrendszer van, amelyben van olyan háromjegyű szám, amelyik kétszer akkora, mint az ugyanezekkel a számjegyekkel ugyanolyan sorrendben felírt tízes számrendszerbeli szám. (4 pont)

JavasoltaProposedBy: Gyanta Nándor, Budapest

B. 3335. A K és L sokszögek úgy helyezkednek el a síkon, hogy csúcsaik nincsenek rajta a másik sokszög oldalegyenesein. Legfeljebb hány pontban metszik egymást az oldalak, ha K ötszög és

a) L háromszög;

b) L négyszög? (5 pont)

B. 3336. Egy szabályos háromszöget a középpontja körül pozitív irányba elforgatunk először 3^o-kal, azután tovább forgatjuk 9^o-kal, majd 27^o-kal, a k-adik lépésben 3^k fokkal. Hányféle helyzetet vehet fel a háromszög az elforgatások eredményeképpen? (3 pont)

B. 3337. Adott egy parabola fókusza és két pontja. Szerkesszük meg a vezéregyenesét. (3 pont)

B. 3338. Oldjuk meg a következő egyenletrendszert:

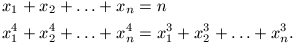(4 pont)

JavasoltaProposedBy: Ábrány Miklós, Ukrajna

B. 3339. Bizonyítsuk be, hogy egy gömbháromszög súlyvonalai egy pontban metszik egymást. (Egy gömb felszínén lévő A és B pontok gömbi összekötő egyenesének az A-t és B-t tartalmazó nem hosszabb főkörívet nevezzük.) (4 pont)

B. 3340. Egy szabályos dobókockát 12-szer feldobva melyik esemény valószínűsége nagyobb?

a) Az első 6 dobás között lesz legalább egy 6-os.

b) A 12 dobás között lesz legalább két 6-os. (4 pont)

B. 3341. Az ABC háromszög A-ból induló magasságának talppontja D. Legyenek E és F egy, a D ponton átmenő egyenesnek olyan -- D-től különböző -- pontjai, amelyekre AE merőleges BE-re, AF merőleges CF-re. A BC és EF szakaszok felezőpontja M, illetve N. Bizonyítsuk be, hogy AN és MN merőlegesek. (5 pont)

X. Ázsiai Matematikai Olimpia feladata

A pontversenyben kitűzött nehezebb feladatok

A. 227. Létezik-e olyan pozitív egész n, amelyre n, 2n, 3n, ..., 2000n mindegyikének tízes számrendszerbeli alakjában a 0-tól különböző számjegyek pontosan ugyanannyiszor fordulnak elő?

A. 228. Igaz-e, hogy ha az f, g: Q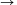Q függvények szigorúan monoton nőnek és értékkészletük a teljes Q, akkor az f+g függvény értékkészlete is a teljes Q? (Q a racionális számok halmaza.)

Fried Ervin, Budapest

A. 229. Két ötszög úgy helyezkedik el a síkon, hogy csúcsaik nincsenek rajta a másik ötszög oldalegyenesein. Legfeljebb hány pontban metszhetik egymást az oldalak?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. február 15.