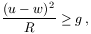A 2000. márciusi számban kitűzött fizika elméleti feladatok megoldásai

P. 3324.  Két autófényszóró-tükröt szembefordítva egymásra helyeztünk az ábrán látható módon. Az alsóban volt egy dugó, a felsőben nem, de úgy látszott, mintha ott is lett volna. Magyarázzuk meg a jelenséget! (4 pont)

Közli: Csonka László, Győr

Megoldásvázlat. A leírt helyzet akkor állhat elő, ha a az alsó tükörben lévő dugó a felső tükör, a felső tükör nyílása pedig az alsó tükör fókuszpontjába esik. Ekkor a dugóról a felső nyílásban valódi kép keletkezik. Ha a tükrök görbületi sugara R akkor a dugó és a nyílás távolsága R/2.

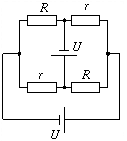P. 3325.  Két-két egyforma ellenállásból és két egyforma telepből az ábrán látható áramkört állítjuk össze. Mekkora áram folyik az r ellenállásokon? (R=20 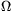, r=10 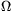, U=10 V.) (4 pont)

Károly Ireneusz verseny, Pécs

Megoldásvázlat. Rajzoljuk át a kapcsolást olymódon, hogy az ellenállások egy négyzet oldalain, a telepek pedig a négyzet átlóiban helyezkedjenek el. Ez a kapcsolás teljesen szimmetrikus a R ellenállások végpontjait felcserélő tükrözésre nézve. Mivel egy ilyen tükrözéskor a R ellenállásokon az áram irányának meg kellene fordulni, ez az áram nulla kell legyen. Eszerint a R elenállások a kapcsolásból elhagyhatók. A maradék áramkörben két r ellenállás van sorba kötve két U feszültségű teleppel, így I=U/r=1 A.

P. 3326.  Egy edényben levő vízben jégdarab úszik. Óvatosan olajat öntünk rá, annyit, hogy éppen ellepje a jégdarabot. Ezután a jégdarab -- miközben a rendszer hőmérséklete állandó marad -- lassan elolvad. Süllyed vagy emelkedik eközben az olaj szintje az edényben? Nő vagy csökken a rendszer gravitációs helyzeti (magassági) energiája? (5 pont)

Közli: Varga István, Békéscsaba

Megoldásvázlat. Mivel az olvadáskor az össztérfogat csökken, az olajszint csökken. A teljes helyzeti energia is csökken: Képzeljük el, hogy a jeget egy vékony merev hártya veszi körül. Ha a jég elovad, a keletkező víz súlypontja lejjebb lesz, mint a jégé volt. Ha a hártya által képezett edény felső kiüresedett részébe olaj áramlik, az olaj súlypontja is lejjebb kerül. Végül a hártya eltávolítása után az olaj-víz felszín kisimulásakor a nehezebb víz lejjebb, a könnyebb olaj helyére kerül, így mindhárom (képzeletbeli) lépésben csökken a helyzeti energia.

Megjegyzés. Van olyan olaj, amely sűrűbb a jégnél (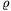_jég=0,92 kg/dm³), vagy vele azonos sűrűségű 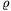_lenolaj=0,93 kg/dm³, 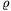_étolaj=0,91-0,92 kg/dm³ (de 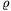_{terpentinolaj}=0,855 kg/dm³). Ha a feladatban a jég az olajon úszik vagy abban lebeg, az eredmény ugyanaz, mint a példában megadott esetben.

P. 3327. Űrsétát végző űrhajóstól eltávolodik űrhajója. Két könnyű, egyforma rugós puskája van, melyekkel két ugyanakkora tömegű lövedéket tud kilőni. Mikor tesz szert nagyobb sebességre, ha azonos irányban egyszerre lövi ki a két lövedéket, vagy ha egymás után? (Legyen például egy lövedék tömege az űrhajós és a két puska tömegének huszad része.) (5 pont)

Közli: Chikán Éva, Budapest

Megoldásvázlat. Ha a kezdetben nyugvó m₁ és m₂ tömegű testeket E energia felhasználásával szétlökjük, a kialakuló sebességek rendre

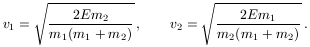
Ennek megfelelően az űrhajós

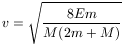
sebességre tesz szert, ha egyszerre süti el a két puskát, míg

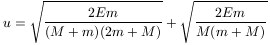
lesz a sebessége, ha egymás után. (Itt E az egy puska elsütésekor felszabaduló energia, az m egy lövedék tömege, M pedig a két puska és az űrhajós együttes tömege.)

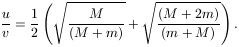
Belátható, hogy ez az arány mindig kisebb 1-nél (adatainkkal pl. u/v=0,9997), az űrhajós tehát akkor tesz szert nagyobb sebességre, ha egyszerre lövi ki a két lövedéket.

P. 3328. Ugyanakkora alapú, de különböző hajlásszögű lejtők közül melyiken csúszik le leghamarabb egy kis test, ha a csúszási súrlódási tényező 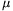? (5 pont)

Közli: Kobzos Ferenc, Dunaújváros

Megoldásvázlat. Legyen a lejtő alapja A. Ha tg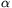>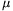, egy test a lejtőn

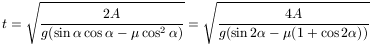
idő alatt csúszik le. Ez az idő annál az 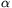szögnél a legkisebb, amelynél a sin 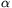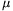2-cos 2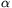 kifejezés a lehető legnagyobb. Bevezetve a 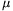=-ctg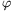 jelölést a fenti kifejezés

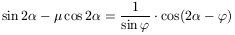
alakra hozható. Ennek maximuma nyilván 2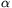= 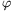szögnél van, tehát a kis test

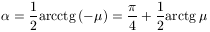
szögű lejtőről csúszik le leghamarabb.

Megjegyzés: A kérdéses szög 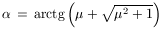alakban is felírható. Súrlódásmentes esetben (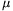=0) az optimális hajlásszög 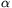=45^o.

P. 3329. Két pici fémgolyócskát egyenként l=0,5 m hosszú fonálon közös pontban felfüggesztettünk. Az egyik golyócska tömege m=2 g, a másiké ennek kétszerese. Mindkettőnek ugyanakkora elektromos töltést adunk. Mekkora ez a töltés, ha a két golyócska egyensúlyban d=20 cm-re helyezkedik el egymástól?

(5 pont)

Közli: Holics László, Budapest

Megoldásvázlat. Egyensúlyban az egyes testekre ható erők eredője nulla, és a két test úgy helyezkedik el, hogy a közös súlypontjuk (az adott d távolságuk mellett) a legmélyebben, tehát a felfüggesztési pont alatt legyen. Eszerint a felfüggesztési ponton átmenő függőleges a d szakaszt 1:2 arányban osztja. Ebből a fonalak függőlegessel bezárt szöge kiszámítható, és így az erőegyensúlyt kifejező egyenletekben szereplő összes mennyiség meghatározható. Az elektromos taszítóerőre

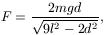
a töltésre pedig

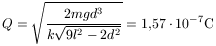
adódik.

P. 3330. p₀ külső légnyomás mellett egy r sugarú szappanbuborékot fújunk. Ha Q elektromos töltést viszünk rá, a buborék sugara R-re nő. Mekkora a szappanoldat felületi feszültsége? (5 pont)

Közli: Légrádi Imre, Sopron

Megoldásvázlat. Egy r sugarú gömb alakú buborékot a felületi feszültség összehúzni igyekszik, ez az összehúzás p=4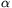/r nyomással képes egyensúlyt tartani. A gömb felületén egyenletesen elosztott Q töltés miatt fellépő Coulomb-erők a gömböt szét akarják feszíteni, ezek az erők p=kQ²/8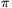r⁴ nyomást tudnak kiegyensúlyozni. A feltöltés előtti és utáni belső nyomást rendre p₁ és p₂-vel, a megfelelő sugarakat pedig r és R-rel jelölve tehát

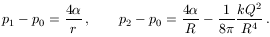
Ehhez hozzávéve az izoterm tágulást kifejező

p₁r³=p₂R³

egyenletet a felületi feszültségre

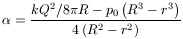
adódik.

P. 3331. Képzeljük el, hogy a világűrben csak egy 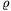₀ sűrűségű homogén gömb van. Egy pillanatszerű robbanás következtében a gömb elkezd tágulni, méghozzá úgy, hogy kezdetben bármely pontjának a középponthoz viszonyított sebessége v₀(r)=H^.r, ahol H a tágulásra jellemző érték, r pedig az adott pontnak a gömb középpontjától mért távolsága.

Legalább mekkora H érték esetén fog ez a gömb a gravitációs vonzás ellenére is örökké tágulni? (5 pont)

Közli: Simon Péter, Pécs

Megoldásvázlat. A centrumtól r₀ távolságra levő részecske csak az r₀ sugarú gömbön belüli tömeg vonzását érzi. Ez a részecske a végtelenségig távolodni fog a középponttól, ha a v₀(r₀)=Hr₀ kezdősebessége nagyobb mint az r₀ sugarú 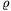₀ sűrűségű gömb alakú test felületéről való szökési sebesség, azaz

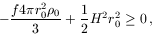ahonnan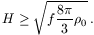

Megjegyzés. Belátható, hogy (az adott kezdeti feltétel mellett) a gömb minden pontja hasonlóan mozog, és emiatt a kezdetben homogén tömegeloszlású gömb tömegeloszlása a mozgás során mindvégig homogén marad.

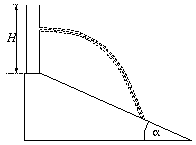
P. 3332.  Egy hosszú, 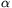hajlásszögű lejtő tetején áll egy H magasságú, henger alakú edény. Az edényt szinültig töltöttük vízzel. Hová fúrjunk lyukat a henger oldalán, ha azt akatjuk, hogy a kiáramló víz a lehető legmesszebb érje el a lejtőt? Ábrázoljuk a becsapódás távolságát a lyuk magasságának függvényében 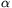=15^o, illetve 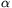=45^o esetén! (6 pont)

Kóbor János, (Miskolc, Földes F. Gimn.) ötlete alapján

Megoldásvázlat. Ha a nyílás a henger tetejétől h távolságra van, a kiömlő víz sebessége .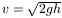

Megjegyzés: A valósághoz közelebb áll az a 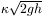kiömlési sebesség-formula, ahol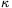 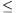1 a nyílás kiképzésétől függő állandó. Az egyszerűség kedvéért a továbbiakban 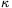-t 1-nek tekintjük.

Koordináta-rendszerünk origójat a kifolyó-nyílás alatt, a lejtő tetején jelölve ki a vízsugár alakját a

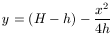
egyenlet adja meg. Ez a lejtőt az (x=s, y=-s tg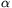) pontban éri el, ahol

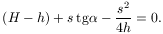
Ez az egyenlet megadja s-et a h függvényében és viszont. Vannak s-ek, amelyekhez két h tartozik, és vannak olyanok, amelyekhez egy sem. Ez utóbbiakat a vízsugár nem tudja elérni! A két tartomány határai (a lejtő egyenesének és a vízsugár parabolájának a lehetséges legszélső metszéspontjai) azok az s-ek, amelyekhez csak egy-egy h tartozik:

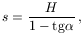
Ebből nyilván az első a ,,jó'', ehhez

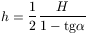
tartozik. Eredményünk addig értelmezhető, amíg h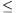H azaz tg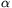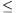1/2, 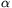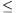26,6^o. Ha ez nem teljesül, a fizikailag megvalósítható helyzetek közül akkor jut el legmesszebbre a víz, ha a lyukat a henger aljába fúrjuk.

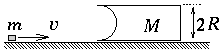P. 3333.  Súrlódásmentes asztalon áll egy M tömegű test, melynek egyik oldalán félhenger alakú mélyedés van az ábra szerint. Legalább mekkora v sebességgel indítsuk el az m tömegű testet, hogy végigfusson az M tömegű test R sugarú bemélyedésén? (A súrlódás mindenütt elhanyagolható.) (6 pont)

Közli: Rácz György, Mezőkövesd

Megoldásvázlat. Ha a m tömeg eljut a körív tetejére, ott a sebessége újra vízszintes, a folyamatot mint egy síma ütközést foghatjuk fel, melyben az impulzus megmarad, de a mozgási energiából 2mRg "elvész". Ennek megfelelően a m és a M tömegek sebessége az ütközés után rendre

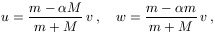ahol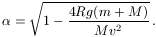

Annak a feltétele, hogy a kis test a körív legfelső pontját is nyomja az, hogy