Matematikából kitűzött gyakorlatok és feladatok
2000. március

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C.575. "Nos, hát mondja meg nekem, hogy ha Pozsonyból Brassóba mindennap két postakocsi közlekednék, Brassóból Pozsonyba pedig ugyanannyi, ha mármost föltesszük, hogy az út tíz napig tart, mennyi kocsival találkozik ön útközben, míg Pozsonyból egy postakocsin ülve Brassóba ér?" 

Javasolta: Mikszáth Kálmán, Fogaras

C.576. Adjuk meg azt a legkisebb pozitív egész számot, amellyel az 1999-et megszorozva a kapott szám utolsó 4 jegye 2001.

Braun Melinda ötlete, Szeged

C.577. Egy fiók mélyén három pár zokni van, amelyek kissé különböznek egymástól. A fiókból egyesével kihalászva a zoknikat, mennyi annak a valószínűsége, hogy három húzás után még nem lesz a kivett zoknik között összetartozó pár?

C.578. Egy háromszög csúcsainak koordinátái: A(2;-1), B(3;1), C(2¹⁹⁹⁹;2²⁰⁰⁰). Számítsuk ki az ABC háromszög területét.

C.579. Egy körlapot két sugara mentén két darabra vágunk. A kapott körcikkekből kúp alakú tölcséreket formálunk. Akkor lesz-e legnagyobb a tölcsérek össztérfogata, ha félkörökből indulunk ki?

A B pontversenyben kitűzött feladatok

B.3352. Ha egy hajó legénységének létszámát megszorozzuk a legénység létszámánál eggyel kisebb számmal, akkor tizenöttel nagyobb számot kapunk, mint ha a kapitány életkorát megszoroznánk a legénység létszámánál kettővel kisebb számmal. Hogy hívják a kapitányt?  (3 pont)

Elhangzott a Repeta című műsorban

B.3353. Mennyi

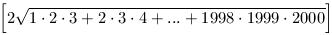
értéke? (Az egész rész jele [ ].) (4 pont)

Javasolta: Ábrány Miklós, Beregszász

B.3354. Adott a síkon két metsző egyenes és egy rajtuk kívül elhelyezkedő P pont. Szerkesszük meg a két egyenesen azt az X ill. Y pontot, amelyre az XY szakasz átmegy P-n és PX^.PY minimális. (5 pont)

B.3355. Bizonyítsuk be, hogy egy háromszög pontosan akkor derékszögű, ha valamelyik két hozzáírt kör sugarának szorzata egyenlő a háromszög területével. (4 pont)

Javasolta: Bíró Bálint, Eger

B.3356. Mutassuk meg, hogy két szomszédos egész szám negyedik hatványának különbsége végtelen sok esetben bontható fel két négyzetszám összegére. (4 pont)

B.3357. Van-e olyan négyzetszám, amelynek ugyanannyi 3k+1 alakú pozitív osztója van, mint 3k+2 alakú? (4 pont)

B.3358. Bizonyítsuk be, hogy 4 különböző valós szám között van olyan kettő: a és b, amelyekre

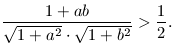
(5 pont)

Mezei József, Vác

B.3359. Bizonyítsuk be, hogy ha az x³-3x-1=0 egyenlet valós x₁, x₂, x₃ gyökeire x₁<x₂<x₃, akkor x₃²-x₂²=x₃-x₁. (5 pont)

Javasolta: Mihalovics Sándor, Esztergom

B.3360. Az ABC háromszög súlypontja S, az AB és AC oldalak felezőpontja E illetve F. Igazoljuk, hogy az AESF négyszög pontosan akkor húrnégyszög, ha AB²+AC²=2BC². (4 pont)

Javasolta: Kiss Sándor, Szatmárnémeti

B.3361. Adottak a G₁ és a G₂ gömbök. Legyen K₁ a G₁ gömbbe, K₂ a G₂ gömbbe írt kocka. Mutassuk meg, hogy annak a 64 vektornak az összege, amelynek kezdőpontja a K₁ egyik csúcsa, végpontja pedig a K₂ egyik csúcsa, nem függ a kockák helyzetétől. (3 pont)

A pontversenyben kitűzött nehezebb feladatok

A.233. Definiáljuk az (a_n) sorozatot a következőképpen: a₀=a₁=1, (n+3)a_n+1=(2n+3)a_n+3na_n-1. Mutassuk meg, hogy a sorozat egész számokból áll.

A.234. Az A, B, és C betűk felhasználásával szavakat (véges hosszúságú betűsorozatokat) készítünk. Egy szóval a következő műveleteket végezhetjük:

a) A szóban kiválasztunk néhány egymás utáni betűt - esetleg csak egyetlen egyet, vagy akár a teljes szót -, és ,,megduplázzuk'', például BBCAC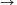BBCABCAC;

b) Az a) lépés visszafelé: Ha valahol a szóban két egymás utáni részlet megegyezik, akkor az egyiket elhagyjuk: ABCABCBC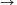ABCBC.

Igazoljuk, hogy ilyen lépések sorozatával bármelyik szóból eljuthatunk egy legfeljebb 8-betűs szóhoz.

A.235. Legyen a adott komplex szám. Mi a mértani helye azon b komplex számoknak, amelyekhez léteznek olyan nemnegatív x₁,x₂,...,x_n valós számok és egységnyi abszolút értékű z₁,z₂,...,z_n komplex számok, hogy x₁+x₂+...+x_n=1, x₁z₁+x₂z₂+...+x_nz_n=a és x₁z₁²+x₂z₂²+...+x_nz_n²=b?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. április 15.

Vigyázat! ,,Áprilisi'' feladat!