A 2000. májusi számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3344. A kerékpárdinamó vízszintes forgó tárcsája az R sugarú kerék tengelyétől r távolságra, pontosan a tengely fölött ér hozzá a kerékhez. A tárcsa és a kerék csúszás nélkül gördülnek egymáson, s a kerék is csúszás nélkül gördül a talajon. Mekkora sebességgel halad előre a tárcsának az érintkezéssel átellenes pontja, ha a kerékpár v sebességgel halad? (5 pont)

Lánczos Kornél verseny, Székesfehérvár

Végeredmény: v(1-r/R).

P. 3345. Egy 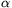=30^o-os hajlásszögű lejtőn lévő, m=6 kg tömegű, r=0,1 m sugarú tömör hengert a palástjához rögzített fonál segítségével tartunk egyensúlyban. A henger a lejtőn nem csúszik meg.

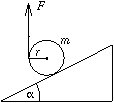
a) Mekkora F erővel tudjuk egyensúlyban tartani a hengert, ha a fonalat függőlegesen tartjuk?

b) Milyen irányban kell húzni a fonalat, hogy a lehető legkisebb erővel tarthassuk a hengert? Mekkora ez az erő?

c) Legalább mekkorának kell lennie a súrlódási együtthatónak az a), illetve b) esetben? (5 pont)

Közli: Kotek László, Pécs

Megoldásvázlat. Jelölje 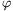a kötél függőlegessel bezárt szögét (úgy, hogy az akkor legyen pozitív, ha a kötél a lejtő felé hajlik)! Az erők és a forgatónyomaték egyensúlyát leíró egyenletek

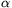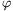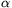+Fcos+Ssin=mg,

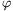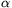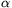Fsin+Scos-Nsin=0

és

(F-S)r=0.

Itt S a súrlódási erő (amely a lejtő mentén fölfelé hat) N pedig az az erő, amellyel a lejtő nyomja a hengert. Ezek megoldása F-re, N-re és S-re

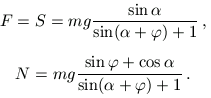
a) Mivel ilyenkor 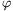=0,

.

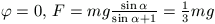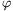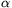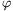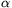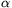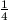b) F akkor a legkisebb, ha a nevező a legnagyobb, azaz sin(+)=1, tehát =90^o- (a kötél párhuzamos a lejtővel). Ilyenkor F=(mgsin)/2=mg.

c) Mivel S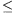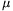N,

.

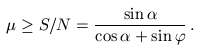A kérdéses esetekben 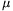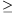tg 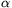=0,58, illetve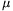 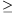(tg 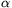)/2=0,29.

A feladat geometriai megfontolásokkal (szerkesztéssel) is megoldaható. Függőleges fonál esetén a nehézségi erő és a fonálerő eredője függőleges, tehát a henger és a lejtő között ható erő is függőleges kell legyen. A minimális súrlódási együttható az érintkező felületek normálvektora és a közöttük ható erő által bezárt szögnek (tehát 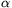-nak) a tangense.

A henger és a lejtő érintkezési pontjára vonatkoztatva csak a nehézségi erőnek és a fonálerőnek van forgatónyomatéka. Az előbbi adott érték, tehát az utóbbi is meghatározott nagyságú. A fonálerő akkor a legkisebb, ha az erőkar a lehető legnagyobb, nevezetesen 2r, s ilyenkor a fonál párhuzamos a lejtő síkjával. A lejtő által kifejtett erő hatásvonalának át kell mennie a nehezségi erő és a fonálerő hatásvonalainak metszéspontján, s ebből a feltételből leolvasható a minimális súrlódási együttható és a fonálerő nagysága is.

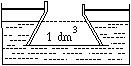P. 3346. Egy csonkakúp-palást alakú, lefelé szélesedő edény fenéklapjához elhanyagolható súlyú, jól illeszkedő korongot szorítunk, majd az edényt az ábrán látható víztartályba merítjük, és a palástjánál fogva a tartályhoz rögzítjük. A kiszorított víz térfogata 1 dm³. Ezután a korongra egy 1 kg-nál kicsit nagyobb tömegű jégdarabot helyezünk. Mi történik, ha a jég elolvad? (Az olvadó jég nem ér hozzá az edény oldalához.) (5 pont)

Közli: Gálfi László, Budapest

Megoldásvázlat. Mivel az edény lefelé szélesedik, a fenéklapot nagyobb erő nyomja felfelé, mint a kiszorított (azaz 1 dm³) víz súlya, így az először megtartja a jeget. Ahogy a jég olvadni kezd, a folyadékfelszín emelkedésével a fenéklapot egyre nagyobb erő nyomja lefelé. Amikor a jég teljesen elolvad, a belőle származó víz térfogata nagyobb, mint 1 liter, tehát az edényben csak úgy férne el, hogy a belső vízszint magasabb lenne, mint a külső. Nyilvánvaló, hogy ez a helyzet nem alakulhat ki, a korong már hamarabb leválik az edény fenekéről. Kérdés: mikor?

Belátjuk, hogy a fenéklap még azelőtt leválik, minthogy a belső folyadékszint elérné a külsőt. Tegyük fel, hogy rögzítjük az edény alját! Amikor a fokozatosan emelkedő belső vízszint éppen megegyezik a külsővel, a jég még nem úszhat. Ha ezt tenné, a belső vízszint a jég teljes elolvadása után is éppen ugyanakkora lenne, mint a külső, de ez ellentmont annak a ténynek, hogy a jég tömege 1 kg-nál nagyobb. (Közismert, hogy egy úszó jégdarab olvadása során nem változik a vízszint.) Azonos külső és belső vízmagasságnál tehát a jég még közvetlenül is ránehezedik a fenéklapra, tehát a fenéklapot lefelé nyomó erő nagyobb, mintha csak a hidrosztatikai nyomás okozná. Ezek szerint mire a belső folyadékszint eléri a külsőt, a fenéklapot belülről már nagyobb erő nyomja lefelé, mint kívülről felfelé, tehát a fenéklapnak --- ha nem rögzítjük --- még azelőtt le kell válnia az edényről, mielőtt a belső folyadékszint elérné a külsőt.

P. 3347. Legalább hányszorosa legyen a fonálinga végén lévő, pontszerűnek tekinthető test tömege a fonál tömegének, hogy az inga lengésideje legfeljebb 1 %-kal térjen csak el a matematikai inga lengésidejétől? (4 pont)

Közli: Simon Péter, Pécs

Megoldásvázlat. Lengés közben a fonal feszes, ezért merev testnek, az inga pedig ``szabályos'' fizikai ingának tekinthető, melynek a lengésideje

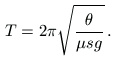
Itt 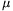=m+M a fonal (m) és a rá akasztott test (M) tömegének az összege, 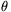=ml²/3+Ml² a teljes tehetetlenségi nyomaték, 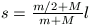a súlypont tengelytől mért távolsága, azaz

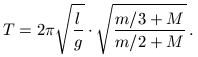
A

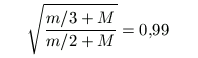
feltételből m/M=0,127 adódik.

P. 3348. Az ábrán látható hosszú, vízszintes sínpárt R ellenállással hidaljuk át. A sínek távolsága l, elektromos ellenállásuk elhanyagolható. A sínpáron súrlódás nélkül csúszhat egy m tömegű, l hosszúságú vezető rúd, függőleges, B indukciójú homogén mágneses térben.

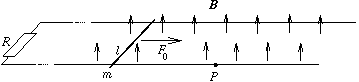
A vezető rúdra már hosszú ideje F₀ nagyságú erőt fejtünk ki, melynek hatására állandósult sebességgel csúszik. Egy bizonyos P pontnál a külső erőhatást megszüntetjük. Mekkora utat tesz meg a vezető rúd a P ponttól a megállásig? (5 pont)

Varga István, Békéscsaba feladata alapján

Megoldásvázlat. Ha az 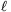hosszúságú vezető rúdban I áram folyik, a B mágneses indukció miatt F=I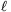B erő hat rá. Másrészről az R ellenálláson eső U=IR feszültség egyenlő a rúdban indukálttal, azaz IR=B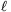v, ahol v a rúd sebessége. Így, az erő és a sebesség iranyát is figyelembe véve a mágneses mező

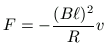
erővel hat a rúdra. A kezdeti állapotban |F|=F₀, tehát a rúd állandósult sebessége v₀=F₀R/(B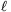)². Ha a rúdra ható külső F₀ erőt megszüntetjük, a mágneses mező által kifejtett erő a rudat fékezi, és az az

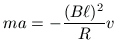
egyenlet szerint lassul. Inen leolvasható, hogy a sebesség 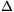s út megtétele alatt

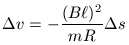
értékkel csökken. Mivel a lefékeződes teljes s útja alatt a sebesség változás éppen -v₀

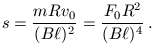
Az

ma=-IB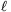

egyenlet hasonló ,,integrálásával'' azt kapjuk, hogy a lefékeződés alatt az R ellenálláson

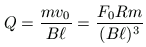
töltés halad át.

P. 3349. Egymástól jó távol helyezkedik el két egyforma szupravezető gyűrű. Az egyik (A) gyűrűben I₀ erősségű áram folyik, a másikban (B) nem folyik áram. A két gyűrűt lassan közelítjük egymáshoz. Mekkora áram fog folyni A-ban, amikor a másik gyűrűben I₁ erősségű áram folyik? (Egy szupravezető gyűrű által körülfogott mágneses fluxus értéke nem változhat meg.) (5 pont)

Közli: Bodor András, Budapest

Megoldásvázlat. Mivel a két gyűrű egyforma, az önindukciós együtthatójuk azonos, L. A kölcsönös indukciós együtthatók mindig azonosak, jelölje ezt L'! Ez az érték a gyűrűk helyzetével és távolságával változik, amíg a gyűrűk egymástól nagyon messze vannak, addig L'=0, de azok közelítésével L' megnő. Az áramokat I_A-val és I_B-vel jelölve az egyes gyűrűk által korülvett fluxusra mindig fennáll, hogy

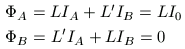
L'-t kiküszöbölve az

I_A²-I₀I_A-I_B²=0

egyenlet adódik, melynek a megoldása I_B=I₁ mellett I_A-ra

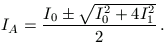
Mivel az I₁ olyan irányú, hogy a fluxusa csökkenteni akarja az A gyűrű fluxusát, a változatlan 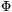_A-hoz I_A-nak nőnie kell, így a felső előjel a helyes, tehát

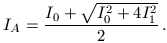
(A másodfokú egyenlet 2 megoldásából úgy is kiválaszthatjuk a fizikailag megfelelőt, hogy megfontoljuk, I₁=0 esetén I_A=I₀ kell legyen.)

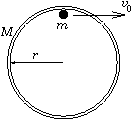P. 3350. Vízszintes asztallapon fekvő M tömegű, r sugarú vékony, keskeny abroncs belsejében, az abroncshoz érintkezve áll egy m tömegű kis test. Hogyan fog mozogni az abroncs középpontja, ha a kis testet érintő irányú, v₀ nagyságú kezdősebességgel elindítjuk? Mennyi idő múlva és hol lesz újra zérus az abroncs sebessége? (A súrlódás mindenütt elhanyagolható.) (5 pont)

Közli: Gnäadig Péter, Budapest

Megoldásvázlat. A tömegközéppont, mely a kis test és az abroncs középpontja közötti távolságot M:m arányban osztja, egyenletes

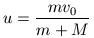
sebességgel halad. Ezt a kis test és az abroncs középpontja

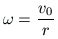
szögsebességgel Mr/(m+M) ill. mr/(m+M) sugarú körön körbe-keringik. Az abroncs újra legközelebb

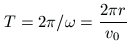
periódus-idő múlva lesz éppen nyugalomban. Eközben az abroncs középpontjának elmozdulása

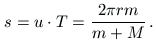
Az abroncs középpontjának pályája ciklois (egy egyenesvonalú egyenletes mozgás és egy ugyanakkora kerületi sebességű egyenletes körmozgás eredője).

P. 3351. v₀ sebességgel, súrlódás nélkül mozgó m tömegű pontszerű test rugalmasan ütközik a k rugóállandójú rugóval összekapcsolt két, egyenként M tömegű, pontszerű testből álló R rendszerrel.

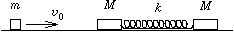
a) Legalább mekkora legyen a m/M arány, hogy egy második ütközés is létrejöjjön az m tömegű test és az R rendszer között?

b) Legfeljebb mennyi idő telik el a két ütközés között? (6 pont)

Francia felvételi feladat (École Normale Superieure, Párizs)

Megoldásvázlat. Közvetlenül az ütközés után a m illetve a baloldali M tömegű test sebessége rendre

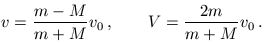
Ettől fogva az R rendszer tömegközéppontja V/2 sebességgel halad, miközben a rendszer

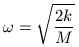
körfrekvenciával úgy rezeg, hogy a sebesség-amplitúdó is V/2. Így a baloldali M tömegű test elmozdulása és pillanatnyi sebessége (az ütközés pillanatát véve t=0-nak)

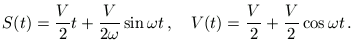
Ugyanakkor a m tömegű test egyenletesen mozog, tehát az elmozdulása

s(t)=vt .

Egy újabb ütközéskor

s(t)=S(t)    azaz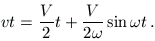    

,,Rendes'' ütközéskor a balról jövő m tömegű test sebessége nagyobb mint az elötte haladó bal oldali M tömegűé, ellenkező esetben a balról jövő test nem képes utolérni a másikat. Határesetben az ütköző testek sebessége azonos (éppen, hogy csak érintik egymást):

v=V(t),    azaz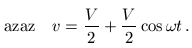    

Innen

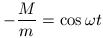    és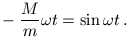    

A két egyenletből kapott 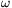t=tg 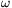t egyenlet megoldásait (2n-1)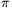/2<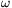t_n<(2n+1)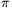/2 szerint indexelve minket az 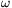t₁ érdekel. Ez numerikusan könnyen megkapható: 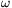t₁=4,4934095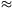4,5. Ebből a kérdéses tömegarány m/M=4,603, és az ütközésig eltelt idő 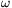ismeretében megkapható.

Megjegyzés: A fenti trigonometrikus egyenlet a következő iterációs eljárással is megoldható. Ha megállapodunk, hogy 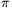/2<arctg x<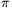/2, akkor az

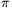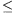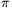x_m+1=+arctg x_m,    0x₀</2

rekurzióval definiált sorozat határértéke éppen

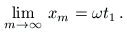
A fenti sorozat nagyon gyorsan konvergál, x₀=0-ból indulva x₈ már a fenti 8 jegyre pontos érték.