 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 216. "Why does a magnetic steel rod have no effect at its middle, but a stronger and stronger effect towards its ends?" - asked Ányos Jedlik (1800 - 1895) famous Hungarian professor of Physics in the course of an examination, in 1871. Measure the direction of the magnetic induction B around a rod magnet and represent the field using B-lines.
New problems:
P. 3344. The horizontal rotating disc of a bicycle dynamo touches the wheel of radius R exactly above the axle of the wheel, at distance r from the axle. The disc and the wheel roll without sliding on each other, and the wheel rolls similarly on the ground. At what speed does the point of the disc opposite to the touching point travel forward when the bicycle travels at speed v?
P. 3345. A solid cylinder of mass
m=6 kg and radius r=0.1 m is kept in balance
on a slope of inclination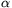 
=30o with the help
of a thread fastened to its jacket. The cylinder does not slip on the
slope.
a) What force F is
required to keep the cylinder in balance when the thread is held
vertically?
b) In what direction should the thread be pulled to minimise the force required to hold the cylinder? What is the magnitude of this force?
c) What is the minimum required coefficient of friction in cases a) and b)?
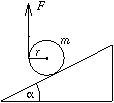
P. 3346. A
well-fitting disc of negligible mass is pressed against the bottom of
a cone-frustum jacket type vessel broader at the bottom. The vessel is
then immersed into the water container shown in the figure and
fastened to the container by its jacket. The volume of the displaced
water is 1 dm3. A piece of ice
with a mass slightly greater than 1 kg is then placed onto the
disc. What happens when the ice melts?
P. 3347. How many times should the mass of the point-like body hanging on a thread be greater than that of the thread so that the period of such a pendulum differs by no more than 1 % from that of a mathematical pendulum?
P. 3348. The long, horizontal pair of rails shown in the figure is connected using resistance R. The distance between the rails is l, the electrical resistance of the rails is negligible. A conducting rod of mass m and length l can slide without friction on the pair of rails, in a vertical, homogeneous magnetic field of induction B.
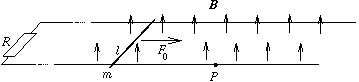
A force of magnitude F0 is exerted for a long time onto the conducting rod, therefore the speed of the rod is constant. The external force stops at a certain point P. What distance does the conducting rod cover from point P before stopping?
P. 3349. There are two identical superconducting rings at a large distance from each other. Current I0 flows in one of them (A), and no current flows in the other one (B). The two rings are slowly approached to each other. What is the current flowing in A when current I1 flows in the other ring? (The value of the magnetic flux surrounded by a superconducting ring cannot change.)
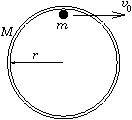P. 3350. A small
body of mass m is at rest inside a thin, narrow tyre of mass
M and radius r lying on a horizontal table, touching the
tyre. How does the centre of the tyre move if the small body starts to
move at a tangential initial velocity v0? How much later and where will the velocity of
the tyre be zero again? (Friction is everywhere negligible.)
P. 3351. A point-like body of mass m moving without friction at speed v0 collides elastically with a system S consisting of two point-like bodies of mass M each, joined to each other by a spring of directional force k.
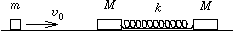
a) What should the minimum value of the proportion m/M be so that a second collision occurs between the body of mass m and the system S?
b) What is the maximum time elapsing between the two collisions?