Matematikából kitűzött gyakorlatok és feladatok
2000. május

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 585. Bizonyos magnókazettákban 0,0075 mm vastagságú szalag tekeredik a 11 mm átmérőjű orsókra. Az orsók középpontjainak távolsága 42 mm. Legfeljebb hány méter szalag lehet egy használható magnókazettában? (A tele orsóról a szalagnak akadálytalanul át kell jutnia az üres orsóra.)

C. 586. Legfeljebb hány oldalú az a konvex sokszög, amelynek nincs két szomszédos tompaszöge?

C. 587. Legyen n pozitív egész. Az x-tengely n abszcisszájú pontját összekötjük az y-tengely n-1 és n+1 ordinátájú pontjaival, továbbá az y-tengely n ordinátájú pontját összekötjük az x-tengely n-1, illetve n+1 abszcisszájú pontjaival. Mekkora területű négyszöget zár közre ez a négy szakasz?

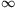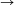C. 588. Írjuk fel az f:(-, -2)R, x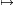2x²+8x+7 függvény inverzét.

C. 589. Egy V keresztmetszetű vízlevezető árokban elakadt egy egyenes bot. A bot két vége az árok két különböző oldalához ér hozzá, és a két oldal síkjával azonos nagyságú szöget zár be. Mutassuk meg, hogy ekkor a bot két vége egyenlő távolságra van az árok aljától.

A B pontversenyben kitűzött feladatok

B. 3372. Egy derékszögű háromszögről tudjuk, hogy a súlyvonalaiból mint oldalakból szerkesztett háromszög is derékszögű. Bizonyítsuk be, hogy a két háromszög hasonló. (3 pont)

Javasolta: Gyanta Nándor, Budapest

B. 3373. Az f egyenes két oldalán, tőle egységnyi távolságra megrajzoljuk az e és g egyeneseket. Legyenek E, F és G a megfelelő egyenesek megfelelő pontjai úgy, hogy az általuk meghatározott háromszögben F-nél derékszög van. Mekkora a háromszög F-ből induló magassága? (3 pont)

Javasolta: Pap Gyula, Debrecen

B. 3374. Egy vizsga két részből áll, írásbeliből és szóbeliből. Mindkét részre 0-tól 9-ig terjedő egész értékű pontszámot lehet szerezni. A rangsorban A megelőzi B-t, ha A eredménye egyik vizsgán sem rosszabb, mint B-é, továbbá legalább az egyik vizsgán A eredménye határozottan jobb. Egy csoport húsz diákja közül semelyik kettő eredménye nem azonos. Bizonyítsuk be, hogy van a csoportban három diák, A, B és C, akik közül A megelőzi B-t és B megelőzi C-t. (4 pont)

B. 3375. Van-e olyan p(x)=x²+ax+b egész együtthatós polinom, amelyre a²-4b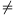0 és p(x) legalább 2000 egész helyen vesz fel négyzetszám értéket? (4 pont)

B. 3376. Az ABC háromszög AC oldala egységnyi. Az A csúcsból induló súlyvonal 1:2 arányban osztja az A-nál lévő szöget. Mekkora lehet a háromszög AB oldala? (3 pont)

Javasolta: Mihalovics Sándor, Esztergom

B. 3377. Legyen k páratlan szám. Mit ad maradékul a 2^n-1k²+2^n-2k⁴+2^n-3k⁸+...+2k^2n-1+k²ⁿ összeg 2ⁿ⁺²-nel osztva? (4 pont)

Javasolta: Bencze Mihály, Brassó

B. 3378. Egy érettségiző osztályban öt egyetemre felvételiznek, mindegyikre a diákoknak legalább a fele. Bizonyítsuk be, hogy van két olyan egyetem, hogy a diákoknak legalább az egyötöde mindkettőre jelentkezik. (5 pont)

B. 3379. Legyen az ABC háromszögben az AA₁, BB₁, CC₁ szögfelezők metszéspontja O. Igazoljuk, hogy 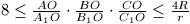, ahol R a köréírt, r a beírt kör sugarát jelöli. (5 pont)

Javasolta: Bencze Mihály, Brassó

B. 3380. Mutassuk meg, hogy minden paralelepipedonban vagy van olyan csúcs, amelynél a három élszög egyike sem hegyesszög, vagy van olyan csúcs, amelynél a három lapszög egyike sem tompaszög. (4 pont)

B. 3381. Az osztályfőnök észrevette, hogy az osztályába járó 30 gyerek között van kettő, akinek ugyanazon a napon van a születésnapja. Mutassuk meg, hogy ez nem is olyan meglepő, hiszen annak valószínűsége, hogy 30 ember között van legalább kettő, akinek egy napon van a születésnapja, legalább 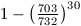. (5 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 239. Szerkesszük meg a háromszöget, ha adott az a három pont, ahol a súlyvonalak meghosszabbításai metszik a körülírt kört.

Javasolta: Rácz János, Budapest

A. 240. Legyenek n és m pozitív egészek. Bizonyítsuk be,

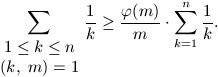
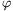( az Euler-féle függvény.)

A. 241. Igazoljuk, hogy tetszőleges n pozitív egész esetén

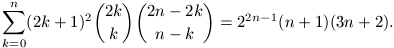
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. június 15.