Solutions for problems "B" in September, 2000

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

B. 3382. The sum of the squares of 17 different positive prime numbers is again a perfect square. Prove that the difference between the squares of the two largest numbers is divisible by the smallest one. (3 points)

Proposed by: A. Gyurcsek, Veszprém

Solution. Dividing a perfect square by 3, the remainder is 0 or 1. Thus, if the sum of 17 perfect squares is another perfect square, then one of the terms is divisible by 3. This implies that one of the 17 prime numbers is 3, and the smallest one is 2 or 3. The two largest primes are not divisible by 2 or 3; they are congruent to 1 modulo 6. So, the difference between the squares of the two largest numbers is divisible by both 2 and 3.

B. 3383. In a right angled triangle, s_a and s_b denote the medians that belong to the legs of the triangle, the median belonging to the hypotenuse is s_c. Determine the maximum value of the expression 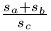. (3 points)

Proposed by: Á. Besenyei, Tatabánya

Solution.

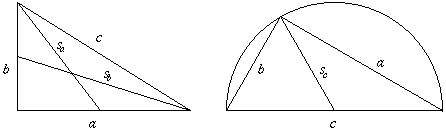
By Pythagoras' theorem

s_a²=(a/2)²+b²,

s_b²=b²+(a/2)²,

and from Thales' theorem

s_c=c/2.

By the inequality of the arithmetic and quadratic mean values,

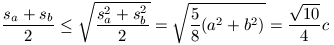
and

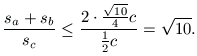
Equality holds if and only if a=b.

B. 3384. Prove that if a, b, c>0, then

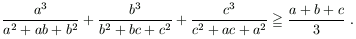(3 points)

Proposed by: M. Ábrány, Beregszász

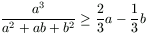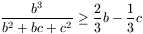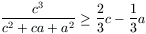Solution. We prove inequalities , and . The sum of them is the statement of the problem.

By the cyclic simmetry it is sufficient to prove the first inequality. This can easily be transformed to 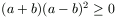, which always holds.

B. 3385. The sides of a triangle ABC satisfy BC=AC+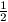AB. Point P divides side AB in the ratio 3:1. Prove that PAC=2(CPA). (4 points)

Solution. Consider the circle k of center C and radius b. Denote the intersection of k and AB by D, the intersection of k and CB by E.

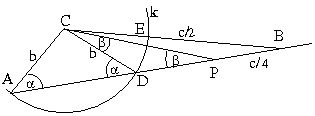
Let k(B) be the power of point B with respect to circle k. Then k(B)=BE^.(BE+2b)=c/2(c/2+2b)=BD^.BA=BD^.c. This implies BD=b+c/4, so PD=BD-c/4=b and DC=b; thus PD=DC, the triangle PDC is an isosceles triangle and finally 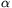=2.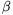

B. 3386. 2001 points are given in a 5x5x10 rectangular box. Prove that there are two of them whose distance is not greater than 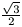. (4 points)

Proposed by: M. Ábrány, Beregszász

Solution. Decompose the box into 2000 cubes, their edges are length of 0.5. There is a cube which contains at least two points. The distance between these points is at least .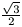

Remark. The 0,866 can be improved, see problem A. 242..

B. 3387. Determine the angle 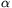if, for some nonzero vector p, the sum of p and the vector obtained from p by rotating it by 2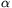 equals to the vector obtained from p by rotating it by . (3 points)

Solution.

For the special case 0^o<<180^o, the configuration is shown in the figure. OA=OC=OB. The quadrilateral OABC is a paralelogramma, AC=OB, so triangle OAC is equilateral. Thus 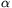=60^o. The 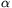can be 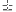60^o+k^.360^o, where k is an arbitrary integer.

B. 3388. In a triangle ABC, the angle at vertex B measures 120^o. The bisector of this angle intersects side AC at point P. The bisector of the exterior angle at vertex C intersects line AB at Q, and finally, segment PQ intersects side BC at R. Find the measure of 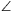PRA. (5 points)

Proposed by: S. Katz, Bonyhád

Solution.

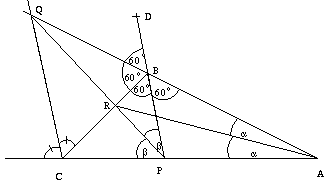
First, consider triangle CPB. QBC=180^o-120^o=60^o. Extend PB to an arbitrary point D. DBQ=60^o, thus BQ is a exterior angle bisector of triangle BCP. The same holds also for CQ; connecting their intersection Q with P, we obtain an angle bisector. Thus CPQ=BPQ:=.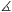

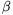Now, consider triangle BPA. The BR and PR are exterior angle bisectors, RA is an angle bisector, thus B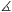AR=PAR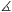:=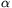. CPB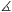 is an exterior angle of triangle PAB so 2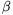=60^o+2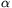, 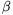=30^o+.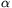

BPA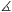=180^o-(60^o+2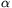)=120^o-2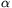

PRA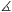=180^o-(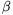+(120^o-2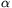)+)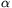=180^o-(30^o+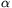+120^o-2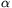+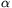)=30^o.

By the solution of Anna Lovrics

B. 3389. Define 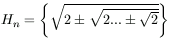, where each surd contains n square root signs. How many different real numbers belong to the set 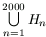? (4 points)

Solution. Let 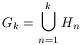. We prove inductively that the set G_k contains exactly 2^k-1 elements, and they lie in the interval (0,2).

In the case k=1, the only element of G_k=H₁ is 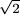, thus our statement is true. Suppose that the statement holds for some k; from this we prove it for (k+1) as well. Decompose the set G_k+1 intu three subsets:

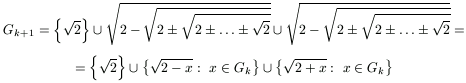
By the induction, the middle term has 2^k-1 elements in interval 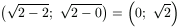; the third term has the same number of elements in interval 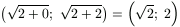. These intervals are disjoint and subsets of interval (0,2). Thus the number of all elements are

1+(2^k-1)+(2^k-1)=2^k+1-1.

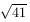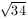B. 3390. In a certain tetrahedron, each vertex is incident to three edges of length 5, and , respectively. Determine the length of each segment between the midpoints of some two opposite edges of the tetrahedron. (5 points)

Solution. It is easy to see that the opposite edges have equal lengths. This implies that the tetrahedron can be inscribed into a rectangular box.

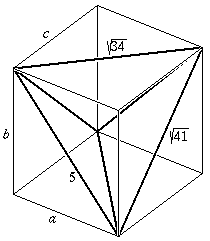
Denote the lengths of the box' edges by a, b and c. By Pythagoras' theorem

a²+b²=25,    b²+c²=41    and    c²+a²=34.

From this system we obtain a=3, b=4 and c=5. The distances between the midpoints of the opposite edges of the tetrahedron are the same.

B. 3391. When Bob, holding his valid reserved ticket, entered the railway carriage, he found, to his utmost surprise, that all the 78 seats had already been occupied. In fact, Dan entered the carriage without a reservation, and the other 77 passengers, including Jim, though having a valid reservation, not necessarily sat on the seats they had booked. Bob immediately asked the passenger occupying his seat to find another seat for himself. Next, the passenger who had to stand up went to his own reserved seat, and so on until Dan got exposed. What is the probability that Jim could remain seated all along? (5 points)

Solution. We assume that the passengers choose their seats randomly, so the probabilities of all possible cases are the same.

Group the possible cases into pairs by the following rule: let each pair contain two cases which differ in only the seats of Jim and Dan, which are exchanged.

Consider a possible case when Dan remains seated. In the pair of this case, Dan has to stand up only after Jim, so Jim must stand up.

Now consider a case when Jim must stand up. In the chain of the passengers which must stand up, Dan is after Jim. If they exchange their seats, Dan will be before Jim and Jim remains seated.

Thus, in each pair, in one case Jim must stand up, in the other case Jim remains seated. The probability that Jim could remain seated is exactly 1/2.

Remark. The solution can be explained in a little different way. If we change the problem such that neither Dan, neither Jim has a valid reservation, the story ends when one of them gets exposed; in the 50% of the cases Dan, in the other 50% Jim.