A 2000. szeptemberi C-jelű matematika gyakorlatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 590. Ismeretes, hogy a Föld felszínén a szabadon eső test
s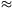 4,903t2 méter utat tesz meg t másodperc alatt. Hogyan módosul a
képlet, ha a távolságot lábban, az időt pedig percben mérjük?
4,903t2 méter utat tesz meg t másodperc alatt. Hogyan módosul a
képlet, ha a távolságot lábban, az időt pedig percben mérjük?
Megoldás. 1 láb körülbelül 0,305 méter. Ezért
s láb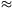 0,305s méter, és
t perc=60t másodperc. Ezeket beírva az eredeti
képletbe, a módosított képlet:
0,305s méter, és
t perc=60t másodperc. Ezeket beírva az eredeti
képletbe, a módosított képlet:
0,305s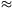 4,903.(60t)2,
4,903.(60t)2,
rendezve
s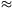 57900t2.
57900t2.
C. 591. Arnold gondolt 5 számot és Bendegúznak megmondta valamennyi összeget, amelyeket két-két szám összeadásával kapott. Ezek a következők: 6, 7, 8, 8, 9, 9, 10, 10, 11, 12. Milyen számokra gondolt Arnold?
Megoldás. Legyen az 5 gondolt szám a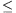 b
b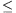 c
c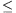 d
d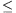 e.
e.
A két legkisebb összeg biztosan a+b és a+c; a két legnagyobb pedig c+e és d+e. Ezért
(1) a+b=6;
(2) a+c=7;
(3) c+e=11;
(4) d+e=12;
Egy további egyenletet például úgy kaphatunk, hogy összeadjuk az összes kéttagú összeget. Mivel mindegyik szám négy kéttagú összegben szerepel, a kéttagú összegek összege 4(a+b+c+d+e):
4(a+b+c+d+e)=6+7+8+8+9+9+10+10+11+12=90,
azaz
(5) a+b+c+d+e=22,5.
Az (1)-(5) egyenletekből a gondolt számok egyértelműen meghatározhatók: a=2,5; b=3,5; c=4,5; d=5,5 és e=6,5. Az ezekből készíthető kéttagú összegek valóban 2,5+3,5=6; 2,5+4,5=7; 2,5+5,5=8; 3,5+4,5=8; 2,5+6,5=9; 3,5+4,5=9; 3,5+6,5=10; 4,5+5,5=10; 4,5+6,5=11 és 5,5+6,5=12.
C. 592. Mennyi az ötjegyű palindrom számok átlaga? (Egy egész szám palindrom, ha visszafelé olvasva önmagát kapjuk.)
Megoldás. Egy ötjegyű palindrom számot egyértelműen meghatároz az első három jegye. Az első számjegy kilencféle, a második és a harmadik tíz-tízféle lehet, tehát 9.10.10=900 ötjegyű palindrom szám van. Az összegüket megkapjuk, ha minden egyes számjegyre megvizsgáljuk, hogy hányadik helyiértéken hányszor szerepel. Mindegyik számjegy ugyanannyiszor szerepel az egyes és a tízezres helyiértékű helyen, méghozzá 10.10=100-szor. Hasonlóan az ezres és a tízes helyiértéken szereplő azonos számjegy 9.10 esetben, a százas helyiértéken szintén 9.10 esetben fordul elő. Ezért az összeg (1+...+9).(10000+1).100+(1+...+9).(1000+10).90+(1+...+9).100.90. Tehát az ötjegyű palindrom számok összege 45.(1000100+90900+9000), ezt el kell osztani 900-zal, hogy megkapjuk az átlagukat, ami 55000.
C. 593. Péter a bélyeggyűjteményéből az 1,2,3,...,37 forintos bélyegek mindegyikéből kivett egy-egy darabot. Szeretné ezeket úgy csoportosítani, hogy mindegyik csoportban ugyanannyi legyen a bélyegek névértékének összege. Hányféleképpen teheti ezt meg?
Megoldás.
C.593. 1+2+...+37=37.38/2=19.37=703. Mivel 19 és 37 prímek, csak 1,19,37 illetve 703 csoportra gondolhatunk. A csoportokban az összeg legalább 37, ezért csak az egyetlen 703 összegű, továbbá a 19 darab 37 összegű csoport lehetséges.
Ha 19 darab 37 összegű csoportot akarunk létrehozni, akkor a 37 forintos bélyeg egyedül alkot csoportot. A többi 18 csoportba külön-külön legalább bélyeg kerül. Mivvel azoban a bélyegek száma éppen 18.2=18, nem lehet kettőnél több elemű csoport. A csoportok tehát csak 37, 36+1, 35+2, 34+3, ..., 19+18 lehetnek.
Összesen tehát kétféle csoportosítás van.
C. 594. Egy húrtrapéz alapja a, másik három oldalának összege d. Mekkorák az oldalak, ha a trapéz területe maximális?
Megoldás. A trapéz csak akkor létezik, ha d>a, mivel két pont között a legrövidebb út az egyenes szakasz. Jelölje x a trapéz szárainak hosszát. Az a-val párhuzamos oldal ekkor d-2x hosszúságú (0<x<d/2).
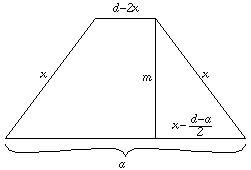
A Pitagorasz-tétel alapján a trapéz magassága
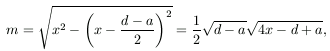
a területe pedig
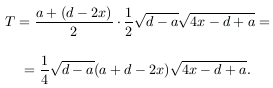
T akkor és csak akkor maximális, ha 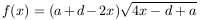 maximális. A szélsőérték helyét differenciálszámítás
segítségével határozzuk meg. f(x) első deriváltja
maximális. A szélsőérték helyét differenciálszámítás
segítségével határozzuk meg. f(x) első deriváltja
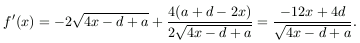
f'(x)=0, ha x=d/3.
0<x<d/3 esetén f'(x)>0, tehát f(x) növekedő,
d/3<x<d/2 esetén f'(x)<0, tehát f(x) csökkenő, ezért x=d/3 esetén lesz f(x) és így a trapéz területe is maximális.

