Matematikából kitűzött gyakorlatok és feladatok
2000. szeptember

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 590. Ismeretes, hogy a Föld felszínén a szabadon eső test s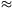 4,903t² méter utat tesz meg t másodperc alatt. Hogyan módosul a képlet, ha a távolságot lábban, az időt pedig percben mérjük?

C. 591. Arnold gondolt 5 számot és Bendegúznak megmondta valamennyi összeget, amelyeket két-két szám összeadásával kapott. Ezek a következők: 6,7,8,8,9,9,10,10,11,12. Milyen számokra gondolt Arnold?

C. 592. Mennyi az ötjegyű palindrom számok átlaga? (Egy egész szám palindrom, ha visszafelé olvasva önmagát kapjuk.)

C. 593. Péter a bélyeggyűjteményéből az 1,2,3,...,37 forintos bélyegek mindegyikéből kivett egy-egy darabot. Szeretné ezeket úgy csoportosítani, hogy mindegyik csoportban ugyanannyi legyen a bélyegek névértékének összege. Hányféleképpen teheti ezt meg?

C. 594. Egy húrtrapéz alapja a, másik három oldalának összege d. Mekkorák az oldalak, ha a trapéz területe maximális?

A B pontversenyben kitűzött feladatok

B. 3382. Bizonyítsuk be, hogy ha 17 különböző pozitív prímszám négyzetének összege négyzetszám, akkor közülük a két legnagyobb négyzetének a különbsége osztható a legkisebbel. (3 pont)

Javasolta: Gyurcsek András, Veszprém

B. 3383. Derékszögű háromszögben s_a és s_b a befogókhoz, s_c pedig az átfogóhoz tartozó súlyvonal. Határozzuk meg az 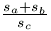kifejezés maximumát. (3 pont)

Javasolta: Besenyei Ádám, Tatabánya

B. 3384. Bizonyítsuk be, hogy ha a, b, c>0, akkor:

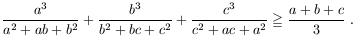(3 pont)

Javasolta: Ábrány Miklós, Beregszász

B. 3385. Az ABC háromszögben BC=AC+ 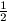AB. P az AB oldal B-hez közelebb eső negyedelőpontja. Bizonyítsuk be, hogy PAC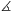 =2CPA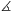. (4 pont )

B. 3386. Egy 5x5x10-es téglatestben adott 2001 pont. Bizonyítsuk be, hogy ki tudunk közülük választani kettőt, amelyek távolsága legfeljebb 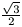. (4 pont)

Javasolta: Ábrány Miklós, Beregszász

B. 3387. Egy nem 0 p vektornak és a 2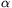 szögű elforgatottjának az összege egyenlő a p vektor 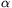szögű elforgatottjával. Mekkora az 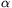szög? (3 pont)

B. 3388. Az ABC háromszög B csúcsánál 120^o-os szög van. Ennek szögfelezője P-ben metszi az AC oldalt. A C csúcsból induló külső szögfelező Q-ban metszi az AB oldal egyenesét, a PQ szakasz pedig R-ben metszi a BC oldalt. Mekkora a PRA szög? (5 pont)

Javasolta: Katz Sándor, Bonyhád

B. 3389. Legyen 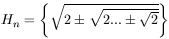, ahol a gyökjelek száma n. Hány valós eleme van az 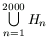halmaznak? (4 pont)

B. 3390. Egy tetraéder minden csúcsában egy-egy 5, 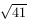és 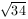hosszúságú él találkozik. Milyen hosszúak a tetraéder szemközti éleinek felezőpontjait összekötő szakaszok? (5 pont)

B. 3391. Amikor Bendegúz érvényes helyjegyével felszállt a 78 személyes vasúti kocsiba, döbbenten vette észre, hogy ott már minden hely foglalt. Az történt ugyanis, hogy Dömötör helyjegy nélkül szállt fel. A többi 77 utas pedig - köztük Elek - vásárolt ugyan helyjegyet, de nem feltétlenül ültek oda, ahová a helyjegyük szólt. Bendegúz felállítja azt, aki a helyét elfoglalta. Aki feláll, az most már szintén a saját helyére szeretne leülni, és így tovább. Mindez addig folytatódik, míg végül Dömötör lelepleződik. Mennyi a valószínűsége annak, hogy Elek ülve nézheti végig az eseményeket? (5 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 242. Egy 5x5x10-es téglatestben adott 2001 pont. Bizonyítsuk be, hogy ki tudunk közülük választani kettőt, amelyek távolsága kisebb, mint 0,7.

A. 243. Határozzuk meg mindazokat a p és q prímszámokat, amelyekre alkalmas n>1 esetén

.

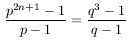Javasolta: Fried Ervin, Budapest

A. 244. Egy számsorozatot nevezzünk Fibonacci-típusúnak, ha a harmadiktól kezdve mindegyik eleme az előző kettő összege. Bizonyítsuk be, hogy a pozitív egész számok halmaza felbontható olyan Fibonacci-típusú végtelen sorozatok uniójára, amelyek közül semelyik kettőnek nincs közös eleme.

Javasolta: Énekes Béla, Tolna

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. október 16.