A 2000 októberi A-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 245. Autónkkal egy kör alakú autópályán kell körbehaladnunk. A pálya mentén bizonyos helyeken benzinkutak vannak, az ezekben található összes üzemanyag két kör megtételére elég. Igazoljuk, hogy a benzinkutak közül kiválasztható legalább egy, amelytől bármelyik irányba elindulva oda visszajuthatunk.
Megoldás. A benzinkutak száma szerinti teljes indukcióval bizonyítunk.
Ha mindegyik benzinkútban elég üzemanyag van ahhoz, hogy bármelyik irányban
eljussunk a következő kútig, akkor az állítás triviális. Feltehetjük tehát,
hogy létezik egy kút a kör A pontjában, ahonnan az egyik irányban nem
juthatunk el a szomszédos kútig, ami B-ben van. A kutakban levő
üzemanyag mennyisége legyen a és b. Feltételezzük, hogy a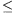 b; ellenkező esetben az A és a B
szerepe felcserélhető.
b; ellenkező esetben az A és a B
szerepe felcserélhető.

Jelölje C azt a pontot, ameddig A-ból B felé elindulva az a üzemanyaggal eljuthatunk. Csökkentsük le az üzemanyag mennyiségét az A illetve B benzinkutakban 0-ra illetve (b-a)-ra, továbbá az AB ívet rövidítsük le az AC távolsággal. Ekkor továbbra is kétszer annyi üzemanyag van, mint amennyi a (lerövidített) kör megtételéhez szükséges, viszont az A benzinkút kiürítése révén a nem üres benzinkutak száma 1-gyel csökkent. Van tehát egy olyan K benzinkút, ahonnan elindulva mindkét irányba körbehaladhatunk. Megmutatjuk, hogy ez a kút az eredeti körön is jó lesz.
Ha K-ból elindulunk valamelyik irányba, akkor előbb-utóbb eljutunk az iránytól függően A-ba vagy B-be; eddig a pontig semmi különbség a kétféle utazás között. Az A vagy B pontba érve az eredeti állapotban a-val több üzemanyagot vehetünk fel, és az AB szakasz is éppen annyival hosszabb, amire ez a plusz üzemanyag elég. Az AB szakasz elhagyása után mindig a-val több üzemanyagunk lesz, mint a lerövidített körön.
A. 246. Határozzuk meg az összes olyan x,y,z,w valós számnégyest, amelyre
x+y+z+w=x7+y7+z7+w7=0.
Shay Gueron, Haifa
Megoldás.
Lemma. Ha a,b valós számok és a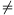 0, akkor az X+Y=a, X7+Y7=b
egyenletrendszernek - az ismeretlenek sorrendjétől eltekintve - legfeljebb
egy valós megoldása lehet.
0, akkor az X+Y=a, X7+Y7=b
egyenletrendszernek - az ismeretlenek sorrendjétől eltekintve - legfeljebb
egy valós megoldása lehet.
Bizonyítás. Legyen X=a/2-Z,
Y=a/2+Z, ahol mondjuk Z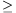 0. Behelyettesítve a második egyenletbe,
0. Behelyettesítve a második egyenletbe,
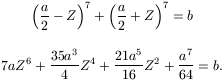
A baloldal Z-ben szigorűan monoton nő, ha a>0, illetve fogy, ha a<0. Ezért legfeljebb csak egy nemnegatív Z-re teljesül az egyenlet. Ezzel a lemma kész.
Megmutatjuk, hogy az (1) egyenletrendszernek azok a számnégyesek a
megoldásai, amelyekben két-két ellentett számpár szerepel. Tegyük fel, hogy
valamelyik két szám összege nem 0, pl. x+y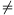 0. Legyen a=-(x+y) és
b=-(x7+y7). A z,w számokra teljesülnie kell a
0. Legyen a=-(x+y) és
b=-(x7+y7). A z,w számokra teljesülnie kell a
z+w=a, z7+w7=b
egyenletrendszernek. Ennek a (-x,-y) számpár megoldása; a lemma szerint más nincs.
Ha az x,y,z,w számok közül bármelyik kettő összege 0, akkor x=y=z=w=0.
A. 247. Igazoljuk, hogy az egységnégyzet oldalegyenesein nincs olyan pont, amely mind a négy csúcstól racionális távolságra van.
Kovács Ádám, Budapest
Megoldás. A megoldás során többször használni fogjuk a következő két - jól ismert - lemmát:
1. lemma. Legyenek az A, B, C pozitív egész számok relatív prímek és A2+B2=C2.
a) Ha A páros, akkor léteznek olyan relatív prím P és Q pozitív egészek, amelyekre A=2PQ, B=P2-Q2 és C=P2+Q2;
b) Ha A páratlan, akkor léteznek olyan relatív prím P és Q páratlan pozitív egészek, amelyekre A=PQ, B=(P2-Q2)/2 és C=(P2+Q2)/2.
Bizonyítás. Az egyenletet átrendezve A2=(B+C)(B-C). Az a) esetben a két tényező legnagyobb közös osztója 2; ekkor alkalmas P, Q pozitív egészekkel B+C=2P2 és B-C=2Q2. Ebből az állítás azonnal következik.
A b) esetben a két tényező relatív prím, külön-külön páratlan négyzetszámok; B+C=P2 és B-C=Q2. Ebből kifejezve az A, B, C számokat, az állítás azonnal adódik.
2. lemma. Ha az A,B,C,D pozitív egészekre AB=CD, akkor léteznek olyan P,Q,R,S pozitív egészek, amelyekre A=PQ, B=RS, C=PR és D=QS. Ha A és B, valamint C és D relatív prímek, akkor az is igaz, hogy a P,Q,R,S számok páronként relatív prímek.
Bizonyítás. Legyen P=(A,C), Q=A/P, R=C/P és S=B/R=D/Q. (Az utolsó egyenlet teljesül, mert B/R=BP/C=ABP/AC=CDP/AC=DP/A=D/Q.) Ezekre az egyenletek teljesülnek, csupán azt kell megindokolni, hogy S miért egész.
A Q és R számok a konstrukció miatt relatív prímek, ezért alkalmas x, y egész számokkal Qx+Ry=1. Ezért S=(Qx+Ry)S=(QS)x+(RS)y=Dx+By egész szám.
Az állítás második fele triviálisan következik abból, hogy A=PQ és B=RS, illetve C=PR és D=QS relatív prímek.
3. lemma. Ha az egységnégyzet valamelyik oldalegyenesén van olyan pont, amelyik mind a négy csúcstól racionális távolságra van, akkor az
(1a) x2+y2=zw; (1b) z2-w2=2xy
egyenletrendszernek van megoldása a pozitív egész számok körében.
Bizonyítás. A pont nem lehet azonos a négyzet egyik csúcsával sem. Nagyítsuk az ábrát fel úgy, hogy a négy távolság egész legyen. Betűzzük a távolságokat az ábra szerint:
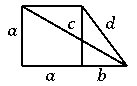
A Pitagorasz-tételből
a2+(a+b)2=c2; a2+b2=d2.
A nagyítás arányát választhatjuk úgy, hogy a és b relatív prímek legyenek. Ezután a és a+b, illetve a és b közül pontosan az egyik páros, a másik páratlan. Mivel a és a+b ellentétes paritású, b páratlan. A második párból pedig a páros.
Az 1. lemma alapján léteznek olyan p,q,r,s pozitív egészek, amelyekre p és q illetve r és s relatív prímek, továbbá
a=2pq, a+b=p2-q2, c=p2+q2
illetve
a=2rs, b=r2-s2, d=r2+s2.
(Ugyanezt kapjuk akkor is, ha a pont az oldal belsejében van.)
Az egyenletekből a-t kifejezve
(2) p2-q2-r2+s2=2pq=2rs.
Mivel pq=rs, a 2. lemma alapján léteznek olyan x,y,z,w páronként relatív prím pozitív egész számok, amelyekre p=xz, q=yw, r=xw és s=yz. Írjuk be ezeket (2)-be:
x2z2-y2w2-x2w2+y2z2=2xyzw;
(3) (x2+y2)(z2-w2)=2xy.zw.
Az x,y,z,w számok között legfeljebb egy páros van. Ha mind a négy szám páratlan, akkor (3) baloldala osztható 4-gyel (sőt 16-tal is), jobboldal viszont nem, ami ellentmondás. Az x,y,z,w számok között tehát van páros. Ekkor (3) jobboldala osztható 4-gyel. A baloldalon az x2+y2 tényező nem lehet osztható 4-gyel, tehát z2-w2 páros. Ebből következik, hogy z és w páratlan, valamint x és y egyike a páros, az x2+y2 tényező páratlan.
Az x2+y2 szám relatív prím a 2xy-hoz, mert relatív prím az x-hez és az y-hoz, ezen kívül páratlan. A z2-w2 szám pedig relatív prím a zw számhoz. Ezért (3) csak úgy teljesülhet, ha x2+y2=zw és z2-w2=2xy, vagyis az (x,y,z,w) számnégyes megoldása az (1a), (1b) egyenleteknek.
4. lemma. Az (1a),(1b) egyenletrendszernek nincs megoldása a pozitív egész számok körében.
Bizonyítás. Tegyük fel, hogy van pozitív egészekből álló megoldás, és tekintsük a "legkisebbet:" azt, amelyben xyzw minimális.
Ha x és y osztható egy p prímszámmal, akkor az (1a) egyenlet alapján z vagy w is osztható vele; viszont az (1b) egyenletből következik, hogy a másik is. Ekkor viszont az összes ismeretlent eloszthatjuk p-vel, és egy kisebb megoldást kapunk. Ezért x és y csak relatív prímek lehetnek.
Hasonlóképpen, ha z és w osztható egy p prímszámmal, akkor 2xy=z2-w2 osztható p2-tel, ebből még p=2 esetén is következik hogy x vagy y osztható p-vel; ezután az (1a) egyenletből kapjuk, hogy x és y is osztható p-vel. Ez szintén ellentmondás, ezért az is igaz, hogy z és w relatív prímek.
A z2-w2=2xy szám páros; ez csak úgy lehet, ha z és w páratlan. Ekkor x2+y2=zw páratlan, vagyis x és y egyike páros. Mivel az egyenletrendszer szimmetrikus x-ben és y-ban, az általánosság korlátozása nélkül feltehetjük, hogy x páros és y páratlan.
Mivel az (1b) egyenlet szerint 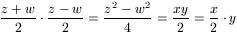 , továbbá
(z+w)/2 és (z-w)/2, illetve x/2 és y
relatív prímek, a 2. lemma alapján léteznek olyan k,l,m,n páronként
relatív prím pozitív egészek, amelyekre
, továbbá
(z+w)/2 és (z-w)/2, illetve x/2 és y
relatív prímek, a 2. lemma alapján léteznek olyan k,l,m,n páronként
relatív prím pozitív egészek, amelyekre
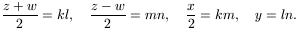
Ezekből x=2km, y=ln, z=kl+mn és w=kl-mn. Helyettesítsük be ezeket az (1a) egyenletbe:
4k2m2+l2n2=k2l2-m2n2;
(4) 5k2m2=(k2-n2)(l2+m2).
A jobboldalon a k2-n2 tényező relatív prím k2-hez, az l2+m2 pedig relatív prím m2-hez. Ezért (4) csak kétféleképpen teljesülhet:
1. eset: k2-n2=m2 és l2+m2=5k2;
2. eset: k2-n2=5m2 és l2+m2=k2.
Az 1. esetben:
(5a) k2-n2=m2, (5b) l2+m2=5k2
Mivel y=ln páratlan, n páratlan. Az (5a) egyenletből
láthatjuk, hogy k páratlan és m páros. Az 1. lemma és (5a)
alapján léteznek olyan  és
és  páratlan pozitív egészek, amelyekre
páratlan pozitív egészek, amelyekre
n=
 m=(
m=( 2-
2- 2)/2, k=(
2)/2, k=( 2+
2+ 2)/2.
2)/2.
Ezt beírva (5b)-be kapjuk, hogy
( 2+
2+ 2)2+(
2)2+(
 )2=l2.
)2=l2.
Ismét az 1. lemma alapján léteznek olyan 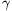 és
és 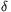 pozitív egészek,
amelyekre
pozitív egészek,
amelyekre
 2+
2+ 2=2
2=2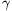
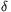 ,
, 
 =
=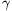 2-
2- 2, l=
2, l=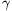 2+
2+ 2.
2.
Az ( ,
,  ,
, 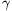 ,
, 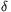 ) számnégyes tehát megoldása az (1) egyenletrendszernek,
ugyanakkor
) számnégyes tehát megoldása az (1) egyenletrendszernek,
ugyanakkor
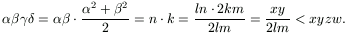
Ez ellentmond annak, hogy az (x,y,z,w) számnégyes minimális megoldás.
2. eset:
(6a) k2-n2=5m2, (6b) l2+m2=k2.
Az előző esethez hasonlóan l páratlan, a (6b) egyenletből m
páros és k páratlan. Az 1. lemma és a (6b) egyenlet alapján léteznek
olyan  és
és  páratlan pozitív egészek, amelyekre
páratlan pozitív egészek, amelyekre
l=
 , m=(
, m=( 2-
2- 2)/2, k=(
2)/2, k=( 2+
2+ 2)/2.
2)/2.
Ezeket beírva (6a)-ba,
( 2-
2- 2)2+n2=(
2)2+n2=(
 )2.
)2.
Ismét az 1. lemma alapján léteznek olyan 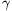 ,
, 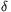 pozitív egészek,
amelyekre
pozitív egészek,
amelyekre
 2-
2- 2=2
2=2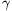
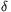 , n=
, n=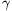 2-
2-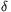 2,
2, 
 =
=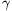 2+
2+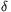 2.
2.
Ebben az esetben a (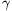 ,
,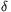 ,
, ,
, ) számnégyes megoldása az (1a),(1b)
egyenletrendszernek, holott
) számnégyes megoldása az (1a),(1b)
egyenletrendszernek, holott
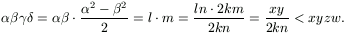
Ezzel a bizonyítás kész.

