 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 218. Prepare a magnetic pendulum. Fasten one of two magnetic discs to a table and hang the other one above the first one in such a way that they are near enough and in an attracting position in equilibrium. Determine the force of attraction acting on the deviated pendulum as a function of the angle of deviation. (6 points)
New problems:
P. 3364. Kalid Kanussi of Morocco covered the distance of 42.195 metres in 2 hours, 5 minutes and 42 seconds at the Chicago marathon, on October 24, 1999. a) How many metres did he `miss' the 2 hours dream record by? (Assume he covered the distance at a constant speed.) b) How much higher should his average speed have been to reach this still unbelievable record? (3 points)
P. 3365. One afternoon Vivien phones Peter to tell him that she has already received the October issue of KöMaL. Peter sets off to Vivien, making 120 steps per minute. He returns home at once and, reading KöMaL, makes 60 steps per minute until he arrives home. How many steps are there between Vivien's and Peter's places if the total time Peter was walking was 30 minutes? (3 points)
P. 3366. In a cubic crystal lattice model consisting of rigid spheres of radius R in contact with each other, what is the radius of the largest sphere that can be placed between these spheres? (3 points)
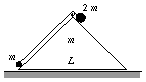P. 3367.
A wooden log of mass m with a cross-section shaped like an equilateral
right-angled triangle can slide on a horizontal surface without friction. Two
point-like bodies of masses m and 2m, tied to each other using a
thread, are placed onto the log as shown in the figure. The length of the base
of the log is L=54 cm. Friction and the masses of the thread and
the pulley are negligible. The bodies are released at a certain
moment. a) What distance does the wooden log cover until the body of
mass 2m reaches its bottom? b) Determine the speed of the
bodies and that of the wooden log when the body of mass 2m reaches the
bottom of the log. (6 points)
P. 3368. There is half a litre of water in a one-litre pot, the bottom of which has an area of 1 dm2. How much work is done while slowly pushing a high beaker with a cross-sectional area of 0.5 dm2 bottom first down to the bottom of the water? (The mass of the beaker is negligible.) (4 points)
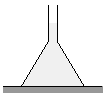P. 3369.
1 dm3 of water is poured into a funnel in
the position shown in the figure. The area of the table covered by the funnel
is 2 dm2, the height of the water is
1.2 dm. What mass should the funnel at least be so that it does not rise
from the table? (4 points)
P. 3370. An experienced pearl-diver swims down to depth h1, then continues sinking without swimming. Arriving at the bottom, he ties a basket of mass m and with an average density twice as high as that of the water to his waist and starts swimming upwards. When reaching depth h2 he does not have to swim any more, he continues rising nevertheless. What is the volume of the lungs of the pearl-diver? (During diving, he never blows out air.) (5 points)
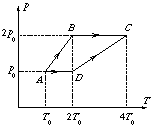P. 3371.
The figure shows two processes of the same N2
gas on a pressure-temperature diagram. In state A the volume of the gas
is V0
a) Represent the processes ABC and ADC in a
pressure-volume diagram.
b) In which process does the gas take up more heat?
c) Determine the proportion of the amounts of heat taken up in the two processes. (4 points)
P. 3372. Two voltmeters with a measuring limit of 30 V and an ammeter with a measuring limit of 1 mA are connected in series to a battery. One of the voltmeters reads 12 V and the other 19 V, while the ammeter reads 0.4 mA. Investigate what happens when one of the instruments is short-circuited. What do the instruments read then? Is any of them damaged? (4 points)
P. 3373. Using the data of the Solar system, show that during the total eclipse of the Sun on the 11 August, 1999, the shade of the Moon run through Hungary at a speed approximately twice as high as that of sound. (4 points)
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.