 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 219. Balance straight rulers (laths) of different lengths on top of a cylinder, in a position perpendicular to the axis of the cylinder. Investigate how the period of the small oscillations of the rulers depends on the length of the ruler. (6 points)
New problems:
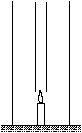 P. 3374. A broad, high glass tube
stands on a table. A candle burns at the centre of the bottom of the tube and
there is a long, narrow glass tube above the candle as shown in the
figure.
P. 3374. A broad, high glass tube
stands on a table. A candle burns at the centre of the bottom of the tube and
there is a long, narrow glass tube above the candle as shown in the
figure.
- a) What happens when the inner glass tube is removed?
b) What happens when the outer glass tube is removed? (3 points)
P. 3375. A certain liquid in a capillary tube rises half as high as water. What happens when some of this liquid is dripped next to one side of a razor blade floating on top of water? (3 points)
P. 3376. One member of a group of tourists, Andrew, walks a little faster than Brian, who started off earlier but walks more slowly. Andrew observes when Brian passes a certain tree and measures (using his watch) that he reaches the same tree time t1 later than Brian, then catches up with Brian after another lapse of time t2. He says that he can work out the proportion vA/vB of their respective speeds using these two time data. How? (3 points)
P. 3377. A shot putter with a mass of 80 kg pushes the iron ball with a mass of 6 kg from a standing position, at an angle of 45o with the horizontal, accelerating it evenly during a time interval of 0.1 seconds. The ball leaves his hand when it is 2 m high above the ground and hits the ground 2 seconds later. What is the minimum value of the static coefficient of friction if the shot putter does not slip during the shot? (5 points)
P. 3378. The plates of a charged plane capacitor are at 3 cm from each other. A 3 mm thick, uncharged metal plate is pushed between them. Do the pd. and energy of the capacitor change? Is any work done while pushing the plate into position? (4 points)
P. 3379. Consumers with respective resistances of 100 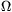 , 200
, 200 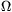 , 300
, 300 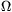 and
400
and
400 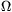 are connected in such a way that
they take up a total power of 100 W when connected to a pd. of
100 V. What power does each consumer take up in this situation? (4 points)
are connected in such a way that
they take up a total power of 100 W when connected to a pd. of
100 V. What power does each consumer take up in this situation? (4 points)
P. 3380. A light source that can be considered as point-like is placed next to a 8.4 mm thick glass panel. Looking at the glass from the side of the light source, at almost right-angles to the glass, several images can be seen at distances of 12 mm from each other. Determine the refractive index of the glass. (5 points)
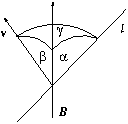 P. 3381. A straight conductor of length
l moves at velocity v in a homogeneous magnetic field of
induction B. What is the pd. between the ends of the conductor if the
angle between the wire and the magnetic induction is
P. 3381. A straight conductor of length
l moves at velocity v in a homogeneous magnetic field of
induction B. What is the pd. between the ends of the conductor if the
angle between the wire and the magnetic induction is 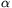 , that between the induction and the velocity is
, that between the induction and the velocity is 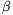 and that between the velocity and the conductor
is
and that between the velocity and the conductor
is 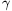 ? (E.g. let
? (E.g. let 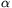 =30o,
=30o, 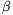 =40o,
=40o, 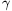 =50o, l=0.5 m,
v=2 m/s and B=0.5 mT.) (5 points)
=50o, l=0.5 m,
v=2 m/s and B=0.5 mT.) (5 points)
P. 3382. Leó Szilárd and Walter Zinn measured that the average number of neutrons produced in the course of the fission of 235U is 2.5. Consider 100 nuclear fissions in an imaginary reactor. Among the neutrons produced in these fissions, 10 escape from the reactor, 8 are captured in 238U, some are absorbed by the control rods and the rest induce further fissions. How many percents of the neutrons have to be absorbed by the control rods in order to sustain a constant number of neutrons in time? (3 points)
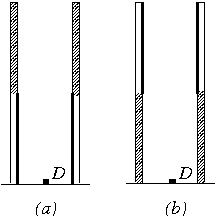
P. 3383. Half of the inner surface of a glass tube is covered with soot, the other half with some reflecting material. The tube is placed vertically onto the table with its black half downward as shown in figure (a). There is a point-like photo-detector D on the table, on the axis of the tube. How many times is the value read by the photo-detector higher when the tube is turned as shown in figure (b)? (5 points)
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.

