Fizikából kitűzött gyakorlatok és feladatok 2001. január

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 221. Mérjük meg, hogy egy lengéscsillapítóval ellátott ajtót mekkora mechanikai munkával lehet teljesen kinyitni! (6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3394. Két autó indul el azonos időpontban, ugyanarról a helyről. Az egyik sebessége 60 km/h, a másik sebessége 80 km/h. Lehetséges-e, hogy az alábbi sebességgel távolodnak egymástól:

a) 140 km/h;

b) 20 km/h;

c) 100 km/h? (3 pont)

Közli: Pécsi István, Szolnok

P. 3395. Egy acél repülőgép-anyahajó hossza a 0 ^oC-os Jeges-tengeren 600 m. Milyen hosszú lesz ugyanez a hajó a 20 ^oC-os Földközi-tengeren? (3 pont)

Közli: Radnóti Katalin, Budapest

Hányszorosára változik a hajó vízbe merülő részének térfogata? (+2 pont)

P. 3396. Az A és B pontokból egyszerre indítunk el egy-egy testet. Az A pontból induló test kezdősebesség nélkül lecsúszik a h=1 m magas lejtőn, a B pontból indulót ferdén elhajítjuk. A két test egyszerre és ugyanakkora nagyságú sebességgel csapódik be a C pontban. Milyen hosszú a lejtő? (A közegellenállás és a súrlódás elhanyagolható.) (5 pont)

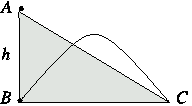
OKTV feladat nyomán

P. 3397.  Az ábrán látható merev, L=2 m hosszú rúd A végpontja állandóan az x tengelyen, B végpontja pedig az y tengelyen mozog. Az A pont sebessége állandó: v_A=1 m/s, és t=0-kor a rúd függőleges.

Határozzuk meg a B pont sebességét, gyorsulását és a rúd szöggyorsulását az idő függvényében. Mekkorák ezek az értékek az alábbi időpillanatokban: t₁=0,5 s, t₂=1,5 s és t₃=1,999 s? (A feladat elemi úton is megoldható.) (5 pont)

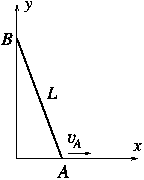
Közli: Holics László, Budapest

P. 3398. Egy korong egyik esetben csak forgó mozgást végez függőleges tengelye körül, másik esetben csak haladó mozgást végez vízszintesen. A két mozgás energiája azonos. A korongot lapjával vízszintes asztalra helyezzük. Melyik esetben áll meg hamarabb? Hányszor hamarabb? (Feltételezhetjük, hogy a korong egyenletesen nyomja az asztalt.) (5 pont)

Közli: Simon Péter, Pécs

P. 3399. Az ábrán látható kerethez nyújthatatlan cérnából kötött hurkot erősítünk és a keretnél fogva szappanoldatba mártjuk. Ha a hurokban levő hártyát kiszúrjuk, a hurok körré feszül ki. Mekkora erő ébred a cérnában, ha a kör sugara 1 cm, az oldat felületi feszültsége 0,03 N/m? (4 pont)

Közli: Sári Péter, Budapest

P. 3400. Acetilén gázzal (c_p/c_V=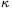=1,25) az ábra szerinti ABCDA körfolyamatot végezzük. Határozzuk meg, hogy a körfolyamat izochor szakaszában a gáz által a környezetnek leadott energia hányszorosa a körfolyamat izobár szakaszán végzett tágulási munkának? (4 pont)

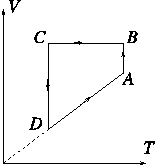
Közli: Légrádi Imre, Sopron

P. 3401. Három azonos, T területű fémlap d₁ és d₂ távolságra helyezkedik el egymástól. Az A jelű fámlap töltetlen, a B és C fémlapok töltése +q és -q. Egy adott pillanatban a K kapcsoló segítségével az A és C fémlapokat egy ismeretlen ellenállású fogyasztón keresztül összekapcsoljuk. Mekkora energiát ad le a fogyasztó a környezetének? (5 pont)

Közli: Kotek László, Pécs

P. 3402.  Ugyanakkora erő hat-e két áramjárta vezető, illetve egy árammal átjárt vezető és egy vele párhuzamos elektronsugár között, ha a többi adat megegyezik? (4 pont)

Közli: Kovács Gyula, Gyömrő

P. 3403. Egy űreszközt szeretnénk a Földről a Marsra eljuttatni úgy, hogy a lehető legkevesebb energiát kelljen befektetnünk. A Földhöz képest mekkora sebességgel kell kilőnünk ezt az eszközt, és a kilövéskor mekkorának kell lennie a Föld--Nap--Mars szögnek? (A Föld és a Mars gravitációs vonzását az objektum pályájának módosításában ne vegyük figyelembe!) (6 pont)

Közli: Nagy Ádám, Budapest, Szent István Gimn.

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. február 11.