 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
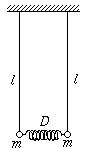
M. 223. Prepare the double pendulum (coupled with a weak spring) shown in the figure and investigate the motions of the system occurring in the plane of the figure. Measure the frequency of beat as a function of l and m. (6 points)
New problems:
P. 3416. On what part of Earth and how can two Sundays be spent between a Saturday and the following Monday? (3 points)
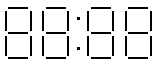
P. 3417. A large digital clock is made to show the hours and the minutes. 14 electric discharge tubes are used to show the minutes, each of which goes out after an average of 2160 hours of operation. The clock is started at 00:00 on the first of January 2001. Which of the tubes showing the minutes can be expected to go out first and when? And which one can be expected to go out last and when? (3 points)
P. 3418. Two circular copper conductors of identical radii and resistances of 30 \(\displaystyle Omega\) each are soldered in such a way that they cross each other's centre. An accumulator of 12 V is connected to the soldered points. a) What is the magnitude of the current flowing through one of the smaller arcs? b) What is the power given out by the accumulator? (3 points)
P. 3419. A hunter hits a bird flying at 100 metres above him, the bird hits the ground at 60 metres from him. Approximately how many metres and how many degrees did the hunter aim in front of the bird if the speed of the bullet was 400 m/s? (4 points)
P. 3420. A long, straight ruler lies on the level table. The ruler is pulled horizontally using a thread attached to one of its ends. Force F0 is required to move the body when the thread is parallel to the longitudinal axis of the ruler. What force is required to move the ruler when the thread is perpendicular to the longitudinal axis? (The ruler presses the table uniformly.) (4 points)
P. 3421. A large group of Alaskan gold diggers arrives at a wide river. They catch sight of a huge nugget on the opposite bank, just in front of them. The digger who arrives first at the nugget will get the right for the exploitation of a mine. What route should Joe choose if he can paddle on the water as fast as he can walk on the ground? Calculate and draw Joe's most favourable route if the proportion of Joe's speed to the speed of the river equals the gold section, is a) greater, b) lesser than the gold section. (Graphical methods can also be used to determine the optimum route.) (5 points)
P. 3422. Nine point-like charges are placed in the points of a 3x3 tetragonal grid with a lattice constant of 1 cm. The magnitude of the charges is chosen in such a way that the potential caused by the other charges at the position of each charge is 10 kV. What is the total interaction energy of the charges? (5 points)
P. 3423. The mobile side of the triangular conducting frame shown in the figure is slid at a uniform speed of v=0.1 m/s along the two other sides. The horizontal frame is in a vertical, homogeneous magnetic field with an induction of B=0.4 T. The length of each side is l=1 m, the resistance is 1 \(\displaystyle Omega\). a) How does the electromotive force induced in the circuit change with time? b) How does the current change with time? c) How much work is required for the sliding if friction is negligible? (5 points)
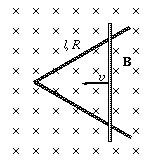
P. 3424. An adiabatically closed system contains two bodies. The heat capacity of body A is 4000 J/K, its temperature is 2400 K, while the heat capacity of body B is 8000 J/K and its temperature is 300 K. What maximum work can be obtained from this system (as heat engine)? (6 points)
P. 3425. What is the picture of the spoked wheel of a bicycle like on a photo finish? (The photo finish is made the following way: pictures of a very narrow band around the finish line are made in very short time intervals using an electronic camera. These are then placed next to each other at distances corresponding to the expected speed of the bicycle.) (6 points)
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.

